题目链接

小L的计数法

分析

首先读完题之后就会发现“若有多组$a_1,a_2…a_k$，输出任意一组均可。”这句话是废话，不可能有多组解，原因如下：

当k位数取最大时，十进制表示为1×1!+2×2!+...+k×k!，
而1!+1×1!+2×2!+3×3!+...+k×k!
=2!+2×2!+3×3!+...+k×k!
=3!+3×3!+...+k×k!
=...=(k+1)!
则最大的k位数与最小的k+1位数差1
故所有数有且仅有一种表示方法

如果只有一种表示方法，可以这样做：
从1开始加，如果不符合<=i的条件，就进位
举个例子：

1表示为1!也就是a1=1
若1要加1变成2，先让a1++,此时a1=2>1，a1=0,a2++，a2=1<=2，满足，故2表示为a1=0,a2=2

如果这样加下去，就可以得到朴素做法

算法1（暴力）$O(N)$

Code:

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL n;
LL a[25],t;//20!明显大于10^18
int main()
{
    LL i;
    cin>>n;
    a[1]=1,t=1;
    n--;
    while(n--){
        LL j=1;
        a[1]++;
        while(a[j]>j){
            a[j]=0;
            a[++j]++;
        }
        t=max(t,j);
    }
    for(i=1;i<=t;i++)cout<<a[i]<<' ';
}

但是这个朴素做法过不了，因为$N$有$10^{18}$
所以要优化，可以先让暴力跑出1~23的表示方法

N=1:1
N=2:0 1
N=3:1 1
N=4:0 2
N=5:1 2
N=6:0 0 1
N=7:1 0 1
N=8:0 1 1
N=9:1 1 1
N=10:0 2 1
N=11:1 2 1
N=12:0 0 2
N=13:1 0 2
N=14:0 1 2
N=15:1 1 2
N=16:0 2 2
N=17:1 2 2
N=18:0 0 3
N=19:1 0 3
N=20:0 1 3
N=21:1 1 3
N=22:0 2 3
N=23:1 2 3

第一位：$101010…$规律变化，和$n$模$2$的值有关
第二位：$112200…$也是规律变化，和$n/2$模$3$的值有关
第三位：$111111222222333333…$，和$n/6$模$3$的值有关
可以推测，第$i$位与$n/(i!)$模$(i+1)$有关，那么就能写出优化代码：

Code:

#include<bits/stdc++.h>
using namespace std;
long long n;
int main()
{
    cin>>n;
    long long s=1,c=1;
    while(n>=s){
        cout<<n/s%(++c)<<' ';
        s*=c;
    }
}

时间复杂度：实际会发现在$N≤10^{18}$阶乘表示法的位数和十进制的位数基本一样，所以可以大概估算成$O(logn)$

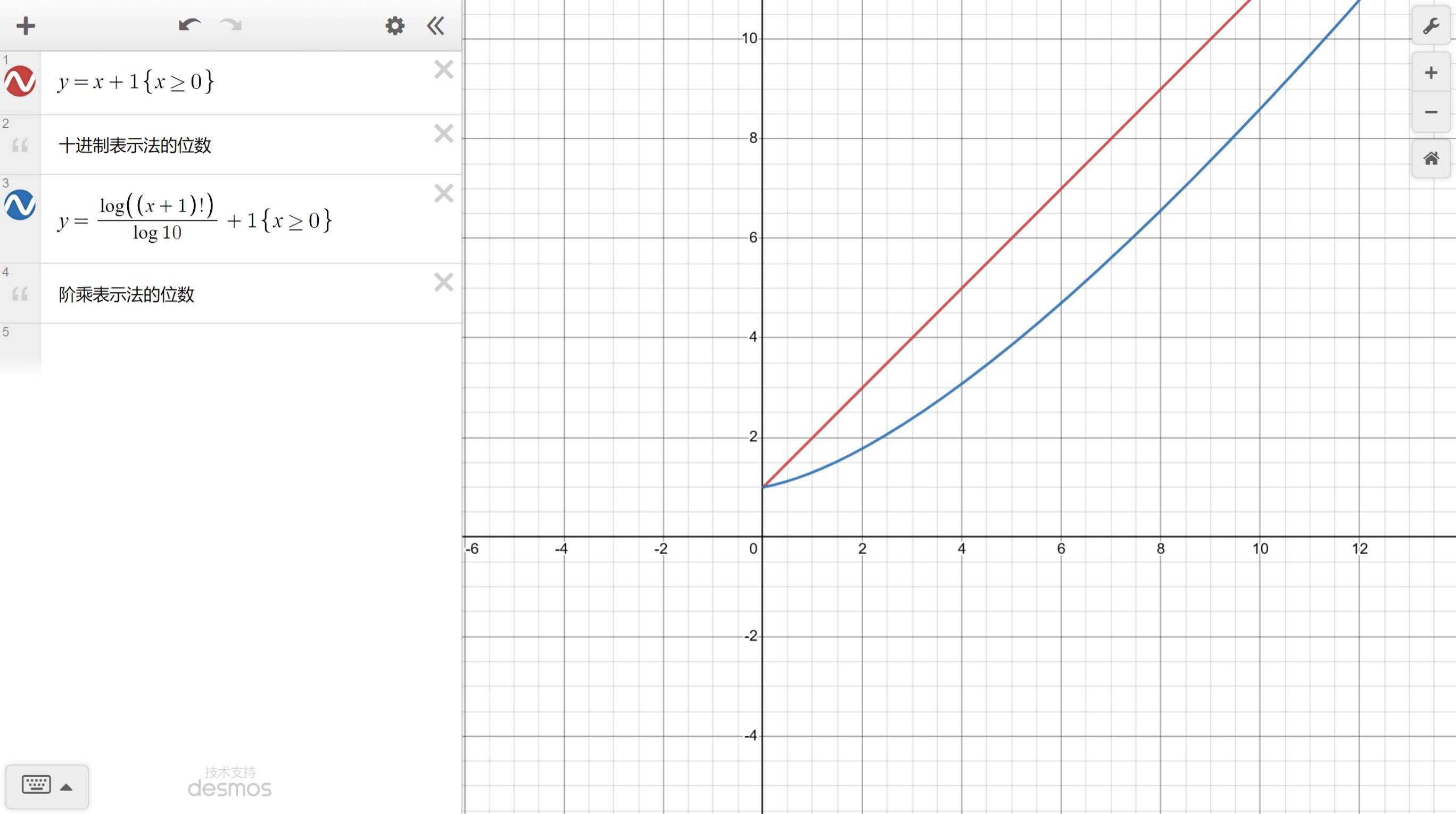
图片展示：