深度优先搜索 DFS
一、DFS 与 BFS 对比
深度优先搜索 ( DFS ) 与 广度优先搜索 ( BFS ) 都可以对整个问题空间进行遍历。
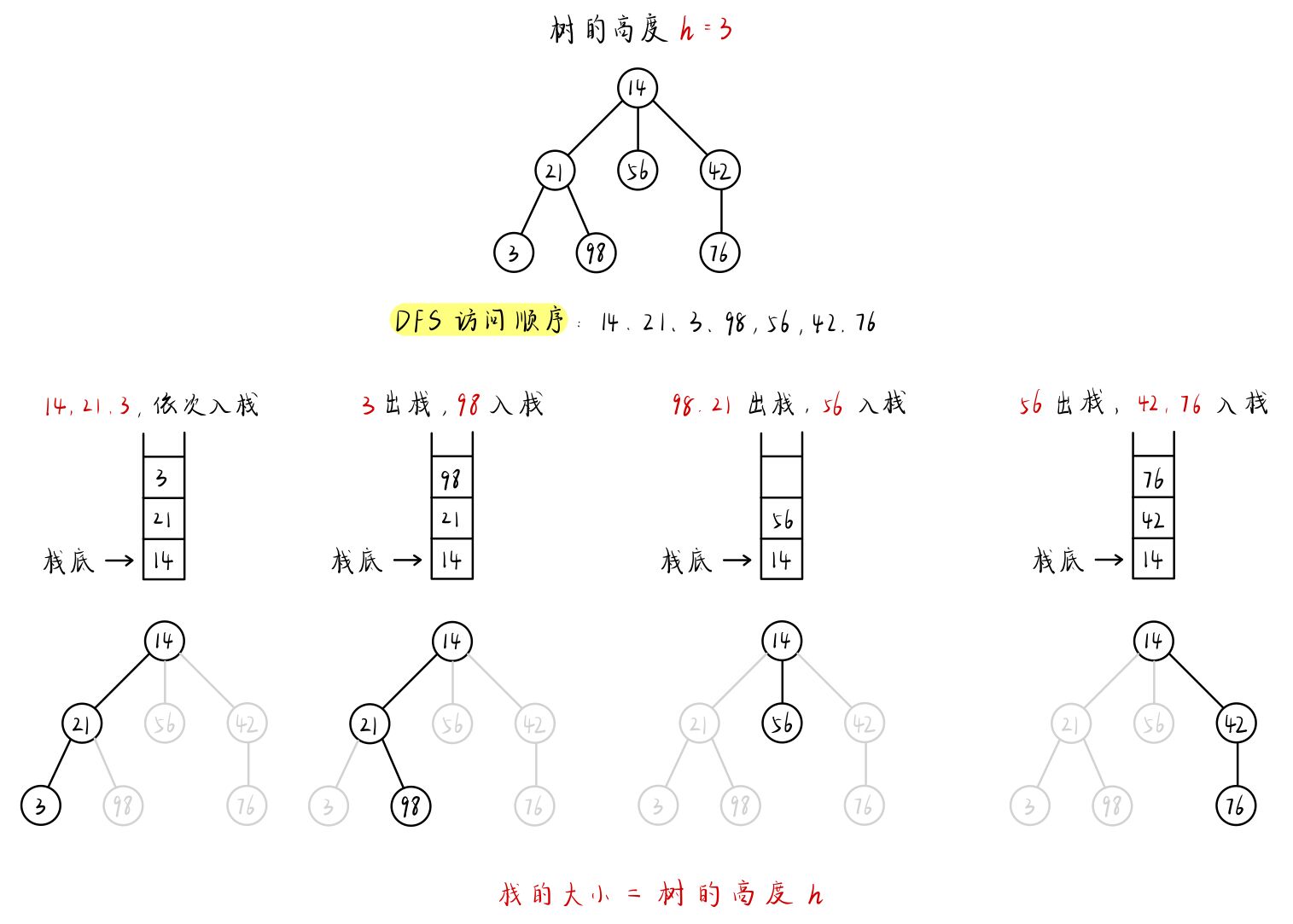
DFS 可以类比为 栈 。
DFS 尽量往 深处 搜索,
每次存储是存储一个路径,因此 空间复杂度 与 树的高度 成正比 O( h )。
 {:height=”50%” width=”100%”}
{:height=”50%” width=”100%”}
BFS 可以类比为 队列 。
BFS 每次要将 下一层 的结点都存储下来,所以空间复杂度为指数级别(某一层中的结点个数)
对于 二叉树,其 空间复杂度 为 O( 2^h )
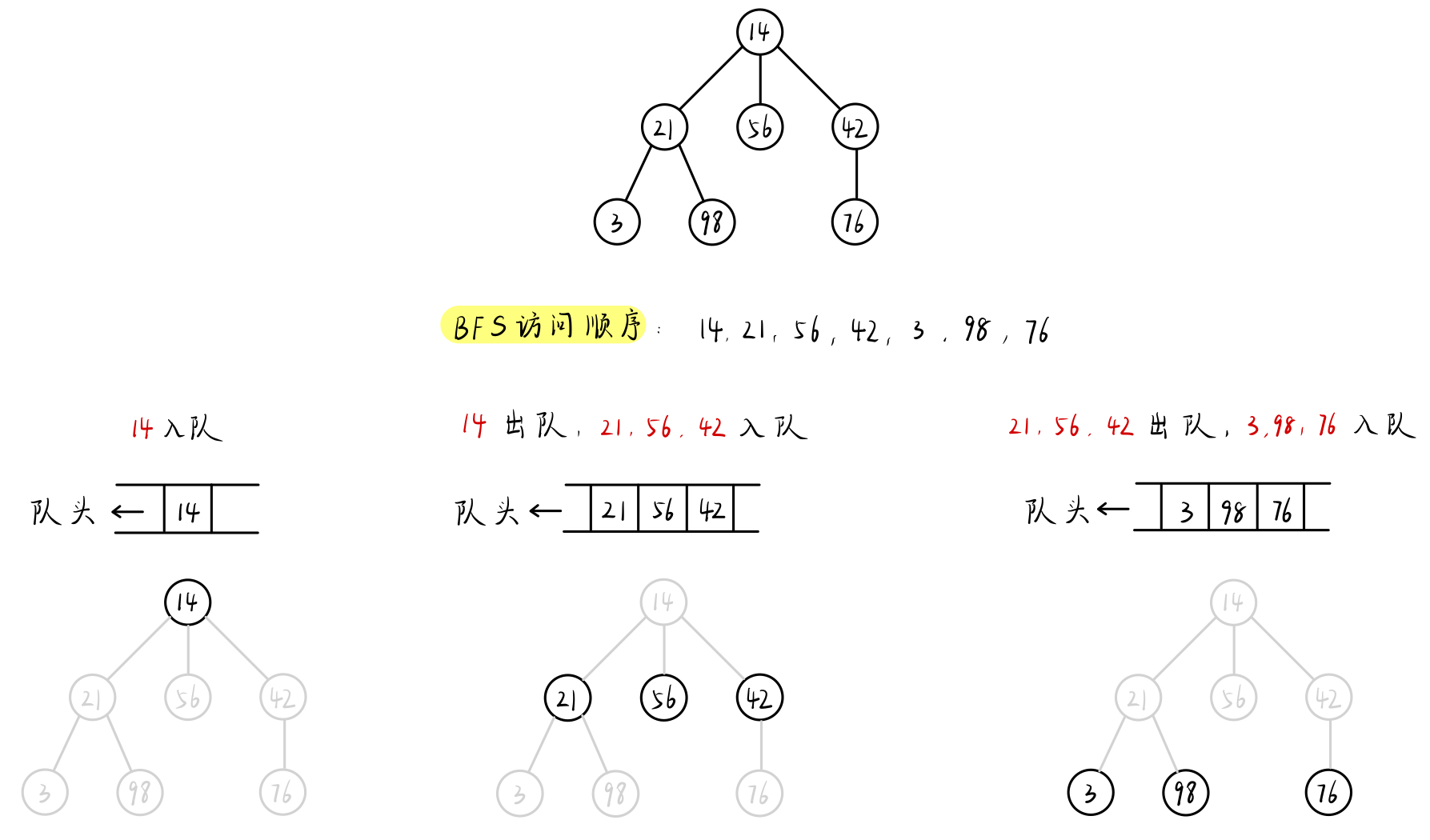
DFS 与 BFS 相比,在空间上有绝对优势。
但 BFS 一层一层地搜索,每次均搜索最近的结点,因此含有 最短路 的思想。
( 当所有 路径的权重均为 1 时,BFS 每次搜索的都是离 当前出发点 最近的结点 )
 {:height=”60%” width=”60%”}
{:height=”60%” width=”60%”}
| 名称 | 数据结构 | 空间复杂度 | 性质 |
|---|---|---|---|
| 深度优先搜索 DFS | 栈 stack | O( h ) 其中 h 为树的高度 | 不具有最短性 |
| 广度优先搜索 BFD | 队列 queue | O( 2^h ) 指数级别 | 具有最短性(总访问最近的点) |
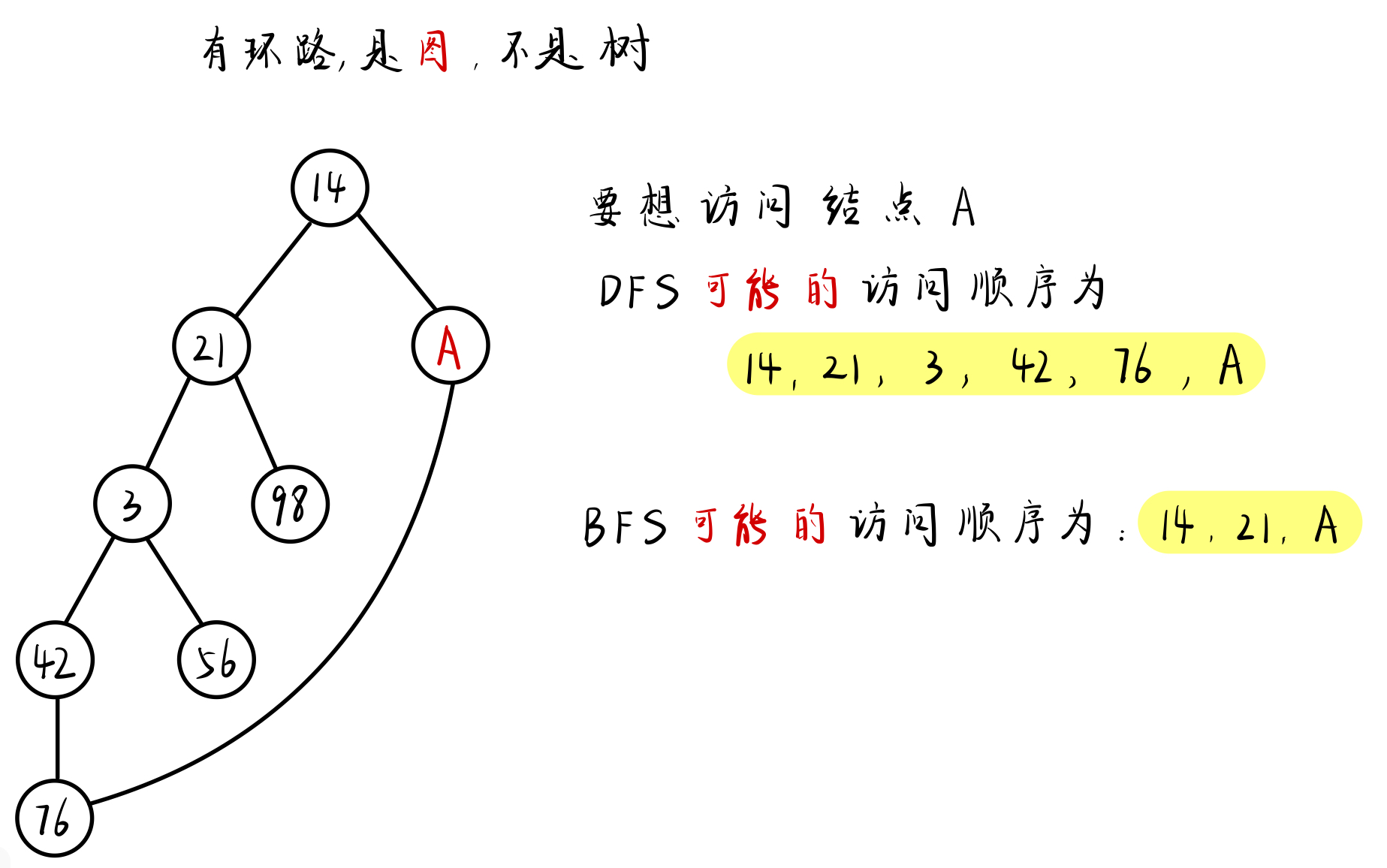
二、回溯
每次 DFS 对应一棵 搜索树( 即 搜索顺序 ),
解题时要考虑的就是 使用什么样的搜索顺序可以把 所有的情况 都遍历一遍。
在遍历的过程中变会发生 回溯 。
DFS 会尽量往深处搜索,当确定当前的点不能再延伸时便会回溯。
回溯要注意恢复现场,即回溯到上一个状态。
 {:height=”30%” width=”30%”}
{:height=”30%” width=”30%”}
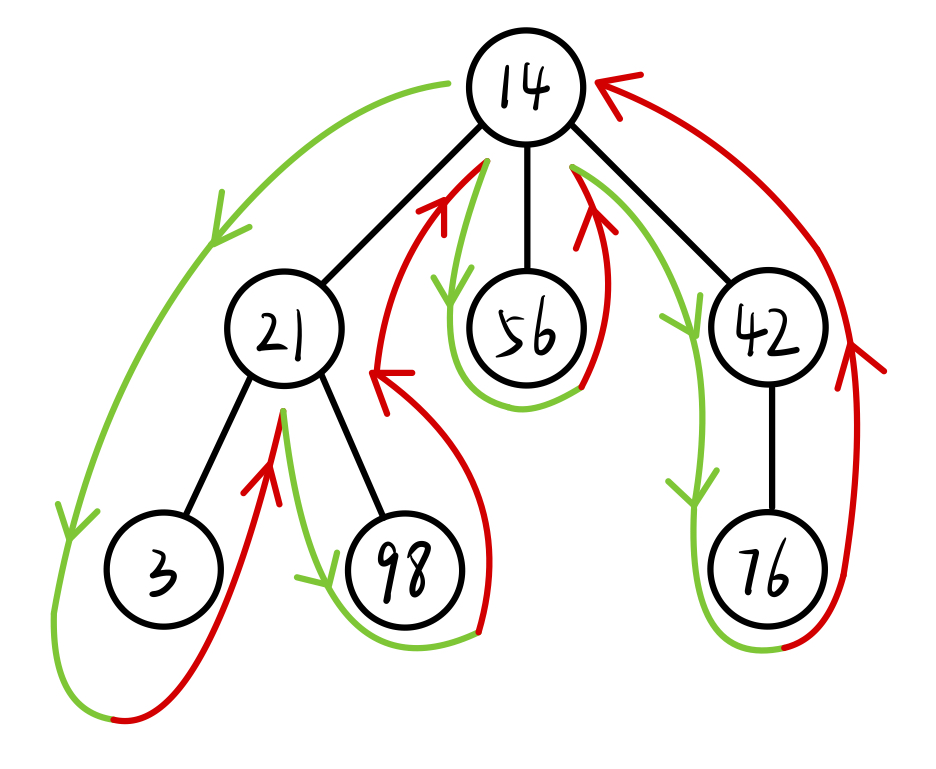
以上述例子为例:
从第一个结点向深处搜索:14 → 21 → 3
到达 3 后,不能再延伸,回溯 到 21
再向深处延伸,→ 98,不能再延伸,回溯 到 2121 之后也不能再延伸,回溯 到 14
14 再向深处延伸,→ 56,不能再延伸,回溯 到 1414 再向深处延伸,→ 42 → 76
76 不能再延伸,回溯 到 42;42 不能再延伸,回溯 到根 14,DFS 结束
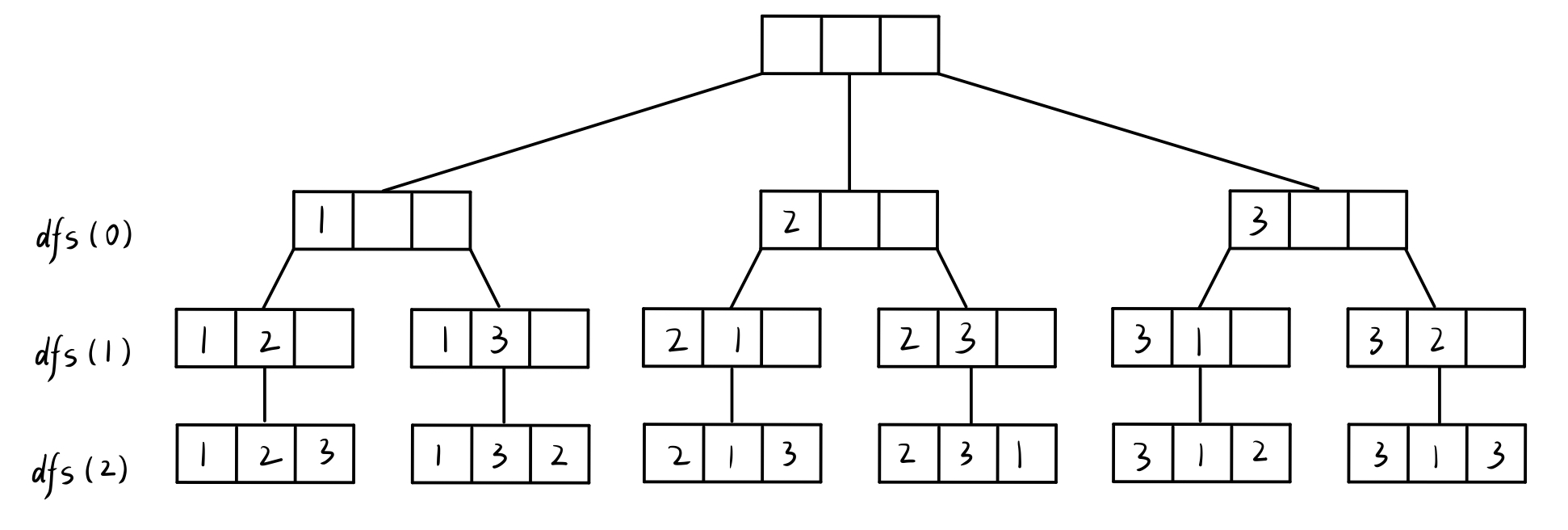
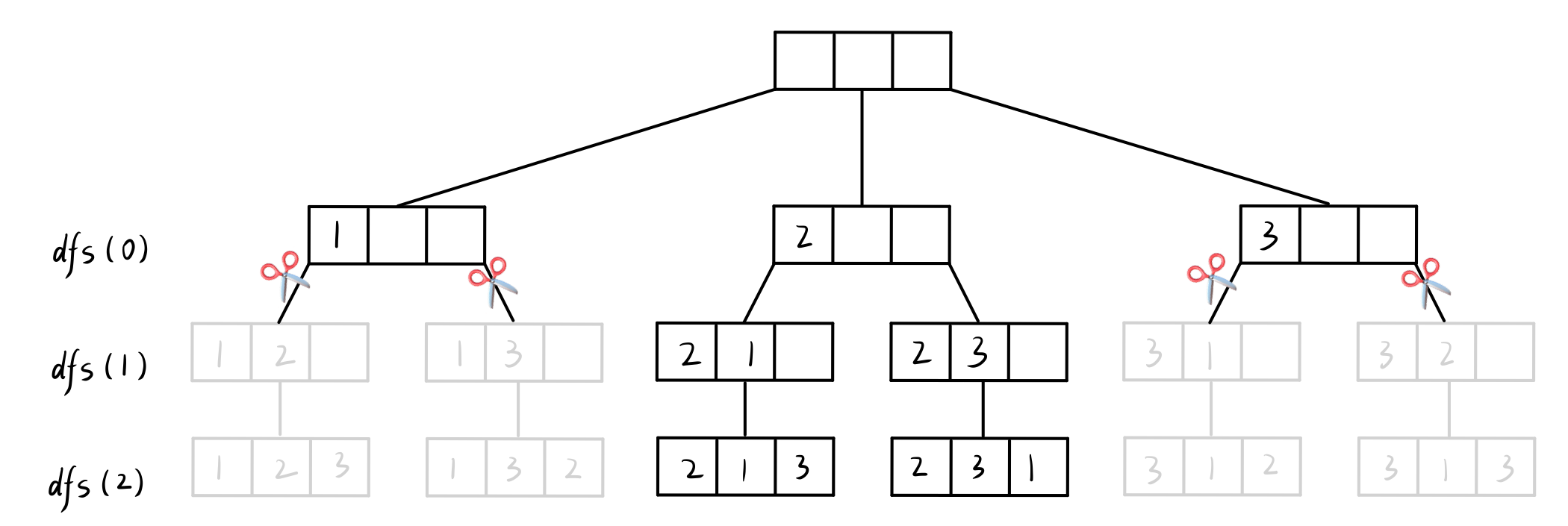
( 1 )应用场景 —— 排列数字(回溯)
输入一个整数 n,以字典序输出 1 ~ n 这 n 个数的全排列。
例如 n == 3
全排列:123 / 132 / 213 / 231 / 312 / 321
( 2 )排列数字 算法思路
n 个元素的全排列,便是将 1 ~ n 这些数,不重复地填入 n 个位置中。
对每个位置的确定可以视作深度优先搜索。
例如 n == 3
确定第一个位置为 1 ( 1 , _ , _ )
再去确定第二个位置,假设为 2 ( 1 , 2 , _ )
再去确定第三个位置,只能为 3 ( 1 , 2 , 3 )不能再拓展,回溯,确定第二个位置为 3 ( 1 , 3 , _ )
再去确定第三个位置,只能为 2 ( 1 , 3 , 2 ),不能再拓展,回溯到第二个位置
仍不能再拓展,回溯到第一个位置,确定为 2 ( 2 , _ , _ )······
-
用
int path[N]数组来存储每个位置上的数字
当path[N]中形成一个结果,即存储了 n 个数,就将结果输出 -
用
bool st[N]数组来记录某个数字是否已经被使用
当st[2] == true,说明数字 2 已经被使用过了
( 3 )排列数字 代码实现
#include <iostream>
using namespace std;
const int N = 10;
int n;
int path[N]; // 存储一条路径上结点的值
bool st[N]; // st[2] == true,说明数字 2 已经被使用过了
void dfs( int u ) // 确定第 u 个位置的数( u 从 0 ~ (n-1) )
{
if( u == n ) // n 个位置都放满了,输出结果
{
for( int i = 0; i < n; i++ ) printf( "%d ", path[i] );
printf("\n");
return ;
}
// 当前位置一共有 n 种选择( 1 ~ n )
for( int i = 1; i <= n; i++ )
{
if( !st[i] ) // 找一个没有用过的元素
{
path[u] = i; // 第 u 个位置确定为 i
st[i] = true; // 数值 i 已经被使用
dfs( u + 1 ); // 确定 下一个 位置(第 u + 1 个位置)
// path[u] = 0; // 恢复现场,但 path[u] 的值会在下个 dfs 中被覆盖,可以省去
st[i] = false; // 恢复现场
}
}
}
int main()
{
scanf( "%d", &n );
dfs(0); // 从 第 0 个 位置开始排
return 0;
}
( 4 )用位运算优化代码
void dfs( int u, int state ) // 确定第 u 个位置的数( u 从 0 ~ (n-1) )
{
if( u == n ) // n 个位置都放满了,输出结果
{
for( int i = 0; i < n; i++ ) printf( "%d ", path[i] );
printf("\n");
return ;
}
// 当前位置一共有 n 种选择( 1 ~ n )
for( int i = 1; i <= n; i++ )
{
if( !( state >> i & 1 ) ) // 找一个没有用过的元素 ***********
{
path[u] = i;
dfs( u + 1, state + ( 1 << i ));
}
}
}
// 调用 dfs( 0, 0 ); 其中 state 初值必须为 0
int state = 0 有 32 位,即 state = 0 D = 00000000 00000000 00000000 00000000 B
第 i 位为 0,则说明数字 i 还没有被使用;
state >> i & 1 用于计算 第 i 位的值,
若为 0,则使用数字 i,并通过 state + ( 1 << i ) 将第 i 位 置 1。
三、剪枝
以 树 的深度优先搜索 为例,
在深度优先搜索中,每次搜索都是 从根结点出发,一直深入到 叶子结点,然后再进行 回溯,去搜索其他方案。
因此在整个过程,把树的 全部结点都遍历了一遍,可能得到 很多搜索结果。
但在众多结果中,有些不是 有效的目标,因此还要进行筛选、剔除。
例如:输入一个整数 n,以字典序输出 1 ~ n 这 n 个数的各个排列,要求 第 1 个数 是 偶数 。
当 n == 3
按照之前的 DFS 得到 全排列:123 / 132 / 213 / 231 / 312 / 321
其中只有 213 / 231 是有效的当 n 很大时,就会发现 近乎一半 的搜索结果都是无效的(第一位为 奇数 的情况)
造成了大量的资源浪费。浪费的原因在于,当我们确定第一个位置为奇数时,
就已经能判定这个方案是错误的,但我们仍继续搜索 第二个位置,… ,第 n 个位置。
想要优化就需要 剪枝 。
剪枝:判断当前方案一定是不合法的,就没有必要再往下搜索了,直接回溯。
( 1 )应用场景 —— n 皇后问题(剪枝)
将 n 个皇后放在 n×n 的国际象棋棋盘上,使得皇后不能相互攻击到,
即任意两个皇后都不能处于同一行、同一列或同一斜线上。
输入: n = 4
输出:
.Q..
…Q
Q…
..Q...Q.
Q…
…Q
.Q..
( 2 )n 皇后问题 算法思路
n 个皇后放入 n * n 的棋盘,每行只能有 1 个皇后,等价于 每一行有且仅有 1 个皇后。
同理,每一列有且仅有 1 个皇后。
因此可以简化题目,1 ~ n 号皇后分别处于 1 ~ n 行,每人只要确定了自己的列号,就能形成一个解。
题目便回到了上述的 n 个数字( 1 ~ n ) 的全排列问题。
 {:height=”70%” width=”70%”}
{:height=”70%” width=”70%”}
但直接搜索出全排列,再剔除不符合条件的情况,便会产生大量浪费,
因此解题的关键在于如何剪枝:
-
不同行:n 个皇后放在 n 行,天然满足条件;
-
不同列:创建
bool col[N],第i列有皇后存在,则col[i] == true; -
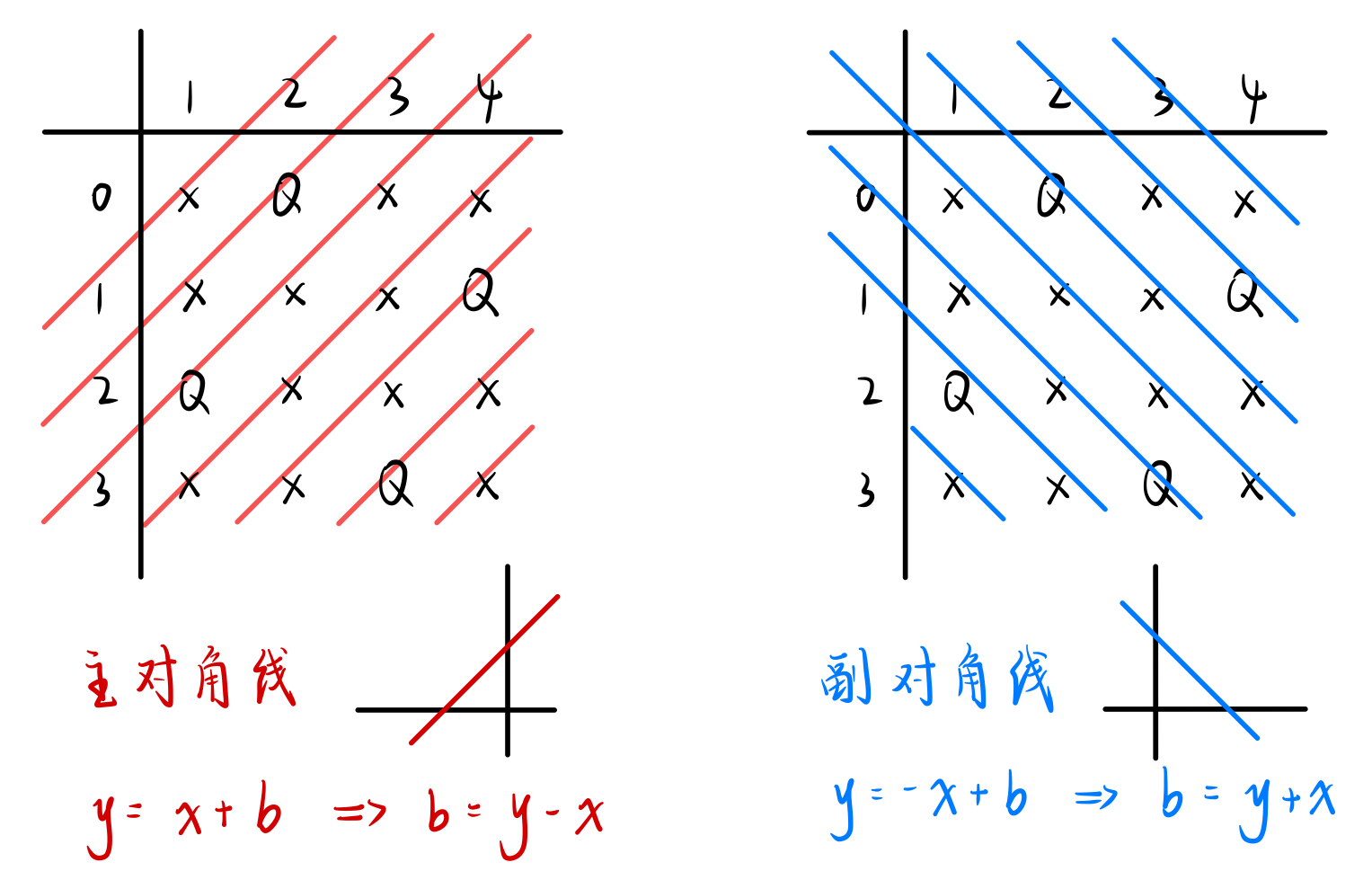
不同对角线:
有两种不同情况的对角线:主对角线、副对角线:
对于同一主对角线上的点,横纵坐标之差( y - x )相同;
对于同一副对角线上的点,横纵坐标之和( y + x )相同。
bool dg[N]; // 主对角线,dg[i] == true,说明该对角线已经被占领
bool udg[N]; // 副对角线
 {:height=”50%” width=”50%”}
{:height=”50%” width=”50%”}
若被访问的位置不满足上述三种条件,则不再深入搜索,完成 剪枝。
( 3 )n 皇后问题 代码实现
#include <iostream>
using namespace std;
const int N = 20; // 开两倍
int n;
char g[N][N];
bool col[N]; // 同一列不能有冲突
bool dg[N]; // 主对角线不能有冲突
bool udg[N]; // 副对角线不能有冲突
void dfs( int x ) // 确定第 x 行中,皇后应该放到哪一列
{
if( x == n ) // n 个皇后位置均已确定,输出结果
{
for( int i = 0; i < n; i++ ) puts( g[i] );
puts("");
return ;
}
for( int y = 0; y < n; y++ ) // 当前位置一共有 n 种选择( 1 ~ n )
{
// 第 i 列位空 && (x,y) 所在主对角线为空 && (x,y) 所在副对角线为空
if( !col[y] && !dg[ x + y ] && !udg[ y - x + n ] )
{
g[x][y] = 'Q';
col[y] = dg[ x + y ] = udg[ y - x + n ] = true;
// 确定下一个(第 x + 1 行)皇后的位置
dfs( x + 1 );
// 恢复现场
col[y] = dg[ x + y ] = udg[ y - x + n ] = false;
g[x][y] = '.';
}
}
}
int main()
{
scanf( "%d", &n );
for( int i = 0; i < n; i++ )
for( int j = 0; j < n; j++ )
g[i][j] = '.';
dfs(0); // 第 1 行下标为 0
return 0;
}
部分代码解析:
c++ const int N = 20; // 开两倍(1 ≤ n ≤ 9)
在 副对角线 udg[N] 中,位置 ( x , y ) 对应的下标为 x + y,因此需要两倍。
!dg[ y - x + n ]
条件判断中,主对角线理论上为 b = y - x,但实际上 y - x 可能变为负数,
而数组的下标是从 0 开始的 非负整数,因此通过 + n 确保下标的非负性。
( 4 )剪枝的两种类型
-
最优性剪枝:判断当前的路径一定不是最优解,剪去;
-
可行性剪枝:判断当前方案一定不合法,剪去。
“不同的题目,搜索顺序可以千奇百怪,因此一个准确的搜索顺序才是解题的本质和关键。”
( 5 ) 补充:n 皇后问题的原始做法
对于 n*n 的棋盘中的每个位置,都有两种可能的情况:放皇后 / 不放皇后。
- 不放皇后,则直接去遍历下一个位置
- 若选择放皇后,则需要判断当前位置是否满足放皇后的条件
- 条件满足,则放,接着去判断下一个结点;
- 条件不满足,放入皇后后,结果一定错误,就不用接着判断了,剪枝。
// n 皇后问题的原始做法
#include<iostream>
using namespace std;
const int N = 20;
int n;
char g[N][N];
bool row[N], col[N], gd[N], ugd[N]; // 行,列,主对角线,副对角线
void dfs( int x, int y, int s ) // x 为行号,y 为列号,s 为已经定位的皇后个数
{
if( y == n ) // 已经遍历完 x 行的每列
{
x++; // 下一行
y = 0; // 重新从第 0 列开始
}
if( x == n ) // 遍历完 x 行
{
if( s == n ) // 已经全部定位完 n 个皇后
{
for( int i = 0; i < n; i++ ) puts( g[i] ); // 输出结果
puts("");
}
return;
}
// ( x, y ) 不放皇后,直接判断下一个格子,定位的皇后数 s 没有变化
dfs( x, y + 1, s );
// 若在 ( x, y ) 放皇后,则要判断该位置是否符合条件
// 若条件满足,接着向后判断,否则剪枝(即不用再向后遍历)
if( !row[x] && !col[y] && !gd[ x + y ] && !ugd[ x - y + n ] )
{
// 符合条件
g[x][y] = 'Q';
row[x] = col[y] =gd[ x + y ] = ugd[ x - y + n ] = true;
// 继续向后遍历
dfs( x, y + 1, s + 1 );
// 恢复现场
row[x] = col[y] = gd[ x + y ] = ugd[ x - y + n ] = false;
g[x][y] = '.';
}
}
int main()
{
scanf( "%d", &n );
for( int i = 0; i < n; i++ )
for( int j = 0; j < n; j++ )
g[i][j] = '.';
dfs( 0, 0, 0 );
return 0;
}
三、参考资料
- y 总的课hh
(接受批评指正,欢迎交流补充~~ XD)


nice,bro
图画的真不错👍