拓扑排序

今天的分享可能有点短。
（众所周知，B站的审核速度=1day，因为没有提前录视频……
我错了别打我

拓扑排序的思路

名人名言一句：

拓扑排序其实就是图的宽搜的应用——强到天下无双的 yxc 巨佬

拓扑图与拓扑序列

首先，有向图才会有拓扑序列。
首先说一下拓扑序列的定义。

若一个由图中所有点构成的序列A满足：对于图中的每条边(x, y)，x在A中都出现在y之前，则称A是该图的一个拓扑序列。

比如说：
在这种情况下，拓扑序列如图所示：

而在这种情况下，不存在拓扑序列。
因为图中存在环。

可以证明有向无环图是一定存在拓扑序列的。
所以这种图也叫拓扑图。

度数

在介绍如何求出拓扑序列之前，我们先来引入一个概念：

度数。

总共分为入度和出度。
入度就是有多少条边指向自己。
出度就是有多少条边出去。

求拓扑序列

拓扑序列中，所有的边都是从前往后的。
因此入读为0的点都可以作为起点。
证明：

  入度为0
->没有任何边指向这个点
->可以作为开头

接下来进行宽搜。

while(q.size())
{
    //弹出队头;
    //枚举t的所有出边（出度）
        //（暴力出奇迹
        //比如t->j
        //删掉t->j
        //相当于以及把t放进拓扑排序最前面，所以没有放的点一定在后面，性质一定满足，删掉
        //if(d[j] == 0) j入队
}

完整流程：

//入读为0的点入队
//while队列不空
    //取出队头t
    //枚举t的所有出边j 
        //删除j
        //if(d[j] == 0)
            //把j入队

所以说拓扑排序还是一个很简单的东西吗。
注意：环上的所有点都不会入队
因为他们的入度都不是0。
这就有点类似病毒的传播（狗头
从一个突破点开始一直突破最后搞定。

注意有一点是这个的根本：

一个有向无环图一定存在一个入度为0的点。

证明：

为了方便理解，增加了图片。

一个有向无环图一定至少存在一个入度为0的点。
反证法：

    假设一个有向无环图所有的点入度都不是0。
    所以我们可以沿着它进来的边找到它的上一个点。

    同样，我们可以继续找到上一个点。

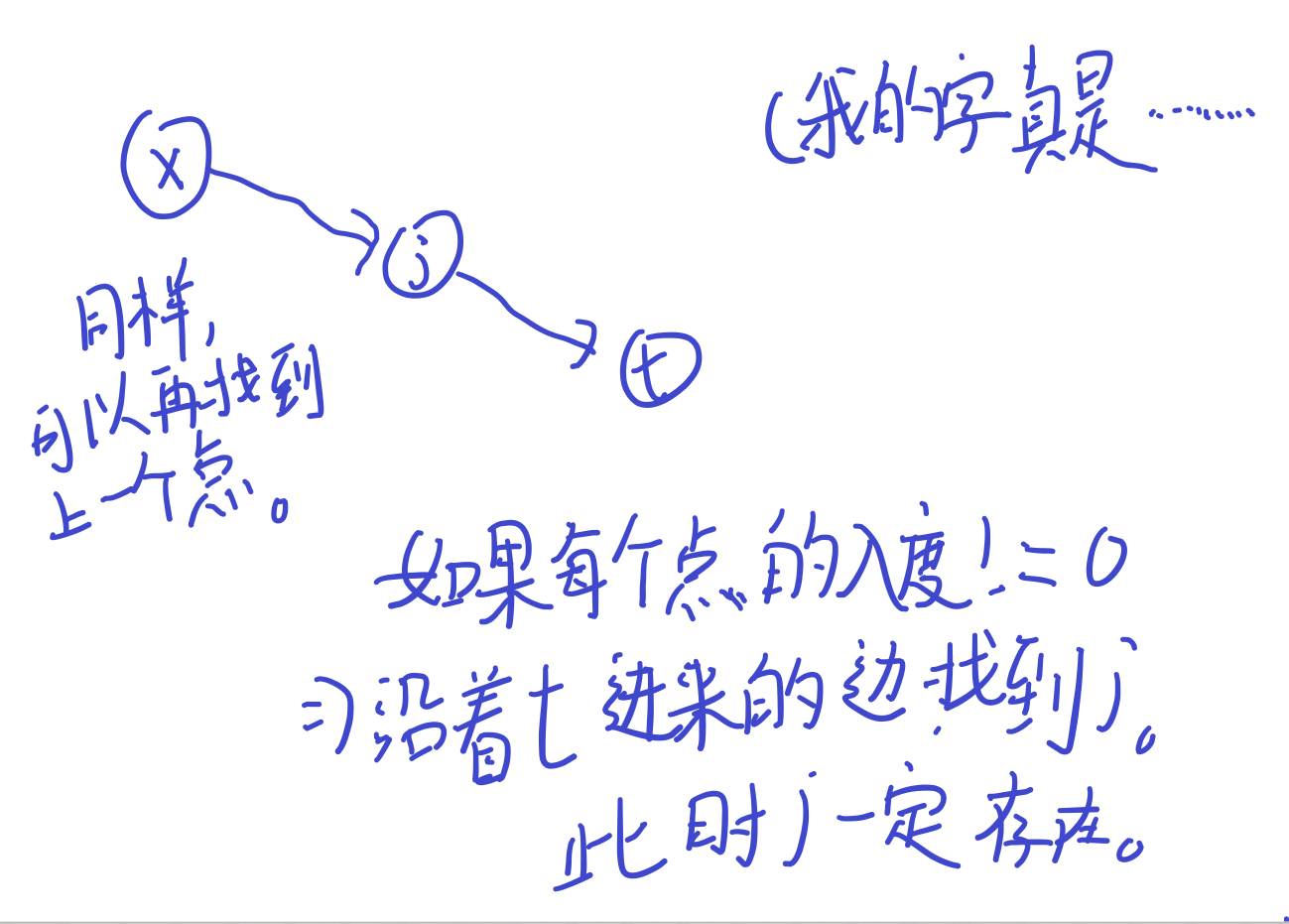
    由于每一个点的入度都不是0，
    所以我每一定是可以沿着它没完没了的找下去的。
    好设点数为m。
    当我们找了m + 1个点后，
    但一共只有m个点，
    根据抽屉原理，
    所以必然存在两个点相同

然后就证明完了。

所以我们就可以从入度为0的点开始不停的删，最后搞定。
(是不是真的很想病毒传播哇
那从开始到结束的序列就是拓扑序列了。

妙哉，妙哉！

拓扑排序的实现

接下来我们按照上面给的列表的顺序搞定拓扑序列。

入度为0的点入队：

for(int i = 1; i <= n; i ++)
    if(!d[i])
        q[ ++ tt] = i;

这里用的模拟队列，按个人习惯。

宽搜模板：

while(hh <= tt)
{
    int t = q[hh ++];

}

遍历t的所有出边。

for(int i = h[t]; i != -1; i = ne[i])
{
    int j = e[i];
}

判断&删除j

if( -- d[j] == 0)
{
    q[ ++ tt] = j;
}

这里不管如何d[j]都会变小，所以j一定会被删除。

return tt == n - 1;

为啥是return这个呢？
其实是为了看看拓扑序列是否存在，
一下为y总的官方解释：

用来判断是否无解。如果tt != n - 1，说明某些点不在队列中，表示无解。——yxc

完整模板：

bool f()
{
    int hh = 0, tt = -1;
    for(int i = 1; i <= n; i ++)
        if(!d[i])
            q[ ++ tt] = i;
    while(hh <= tt)
    {
        int t = q[hh ++];
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if( -- d[j] == 0)
            {
                q[ ++ tt] = j;
            }
        }
    }
    return tt == n - 1;
}

作者：cht
链接：https://www.acwing.com/activity/content/code/content/336002/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

这个是看有没有拓扑序列，如果有，拓扑序列存在q数组里。
接下来我们看一下拓扑序列的完整例题：
有向图的拓扑序列
给定一个n个点m条边的有向图，点的编号是1到n，图中可能存在重边和自环。

请输出任意一个该有向图的拓扑序列，如果拓扑序列不存在，则输出-1。

若一个由图中所有点构成的序列A满足：对于图中的每条边(x, y)，x在A中都出现在y之前，则称A是该图的一个拓扑序列。

输入格式
第一行包含两个整数n和m

接下来m行，每行包含两个整数x和y，表示存在一条从点x到点y的有向边(x, y)。

输出格式
共一行，如果存在拓扑序列，则输出拓扑序列。

否则输出-1。

数据范围

1≤n,m≤${10}^5$

输入样例：

3 3
1 2
2 3
1 3

输出样例：

1 2 3

这道题就是加上了main函数，代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, m, h[N], e[N], ne[N], d[N], q[N], idx;
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
bool f()
{
    int hh = 0, tt = -1;
    for(int i = 1; i <= n; i ++)
        if(!d[i])
            q[ ++ tt] = i;
    while(hh <= tt)
    {
        int t = q[hh ++];
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if( -- d[j] == 0)
            {
                q[ ++ tt] = j;
            }
        }
    }
    return tt == n - 1;
}
int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for(int i = 0; i < m; i ++)
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
        d[b] ++;
    }
    //注意这里初始化时别忘了看看入度是多少！！！
    if(!f()) cout << "-1 ";
    else{
        for(int i = 0; i < n; i ++) cout << q[i] << ' ';
    }
    cout << endl;
    return 0;
}

好了今天的分享就到这里了。

今日起，cht讲开始一边更新提高课搜索一边更新基础课数论

这是我的全部分享

bye~