质数

试除法判定质数

根据质数的定义，对于n遍历2~n-1，如果存在x有n%x==0则不是质数，否则是质数。
遍历优化：只遍历2~√n即可。(因为n的因数范围是1~√n)

分解质因子

一个数字n一定能够分解成它质因数的乘积。（质因子可能包含本身如5）。
分解质因子遍历2~√n，如果n%i==0则i一定是质因子，对于质因子i要不断n/=i来筛除i的倍数。
性质：n最多有一个大于√n的质因子。

朴素筛质数

对于任何一个数字i，筛除所有i*k。没被筛除的是质数。

质数筛质数

仅对质数i，筛除所有i*k。没被筛除的是质数。

质数+范围筛除质数

对于数字i，筛除数字prime[j]*i，当i%prime[j]==0退出。

约数

试除法求约数

约数是成对出现的，对于n遍历1~√n来得到约数i和n/i，注意i!=n/i

约数个数

由于数字x=(p1^n1)(p2^n2)(p3^n3)..，所以每个括号确定一个数字多个括号间相乘得到一个约数，一共有(n1+1)(n2+1)(n3+1)..种组合方式。

约数之和

由于数字x=(p1^n1)(p2^n2)(p3^n3)..，所以(p1^0+p1^1+…+p1^n1)(p2^0+p2^1+…+p2^n2)(p3^0+p3^1+…+p3^n3)…<=>约数之和。

gcd

gcd(a,b)=gcd(b,a%b);当b==0,return a;

欧拉函数

求质因子然后代入公式。

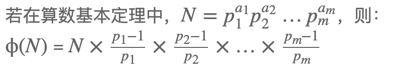
快速幂

a^bmodc，a^b=a^x1*a^x2…，其中b=x1+x2+..，即只计算b的二进制中为1的项与对应的位权。