博弈论是二人在平等的对局中各自利用对方的策略变换自己的对抗策略，达到取胜的目的。

1928年，冯·诺依曼证明了博弈论的基本原理，从而宣告了博弈论的正式诞生。

前置

有限的：无论两人怎样决策，都会在有限步后决出胜负。
公平性：即两人进行决策所遵循的规则相同。

P/N状态

P-position：P代表Previous，上一次行动的人有必胜策略的局面是P-position，也就是“先手必败”

N-position：N代表Next，当前行动的人有必胜策略的局面是N-position，也就是“先手可保证必胜”

• 无法进行任何移动的局面（即terminal position）是P-position
• 可以移动到P-position的局面是N-position
• 所有移动都导致N-position的局面是P-position

P点：即必败点，在双方都在最优策略下，玩家位于此点必败
N点：即必胜点，在双方都在最优策略下，玩家位于此点必胜

胜态与必败态

• 若面临末状态者为获胜则末状态为胜态，否则末状态为必败态
• 一个状态是必败状态，当且仅当它的所有后继都是必胜状态

• 一个状态是必胜状态，当且仅当它至少有一个后继是必败状态

• 我们可以在状态图上，按照拓扑排序的逆序，判断每个点的状态，向前递推

例题：P1288 取数游戏II

有一个取数的游戏。初始时，给出一个环，环上的每条边上都有一个非负整数。这些整数中至少有一个 $0$。然后，将一枚硬币放在环上的一个节点上。两个玩家就是以这个放硬币的节点为起点开始这个游戏，两人轮流取数，取数的规则如下：

（1）选择硬币左边或者右边的一条边，并且边上的数非 $0$；

（2）将这条边上的数减至任意一个非负整数(至少要有所减小)；

（3）将硬币移至边的另一端。

如果轮到一个玩家走，这时硬币左右两边的边上的数值都是0，那么这个玩家就输了。

如下图，描述的是 Alice 和 Bob 两人的对弈过程，其中黑色节点表示硬币所在节点。结果图 $(d)$ 中，轮到 Bob 走时，硬币两边的边上都是 $0$，所以 Alcie 获胜。

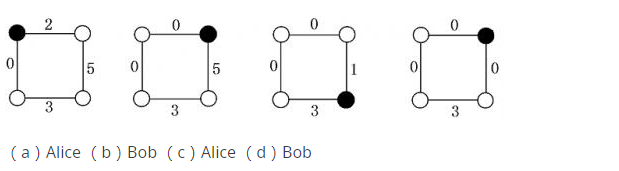
现在，你的任务就是根据给出的环、边上的数值以及起点（硬币所在位置），判断先走方是否有必胜的策略。

分析：

• 环上至少有一个 $0$，把对手逼到 $0$ 位置，把回来的路上的硬币都拿掉，对手会失败
• 先手可以决定走的方向，沿着某个方向走，并且沿着某个方向走，并且把硬币拿光，则对手无法往回走。
• 对于一条链 2 5 3 0，先手把 $2$ 拿光，后手无论取多少，先手再把 $3$ 拿光就赢了。所以发现链上的边数是奇数的时候，先手必胜，反之先手必败。
• 环上有两个方向，两个方向如果有一个必胜，则先手可以决定沿着这个方向走，必胜。反之必败。

代码实现

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::min;
using std::abs;
using std::vector;
using ll = long long;

int main() {
    int n;
    cin >> n;

    vector<int> a(n);
    rep(i, n) cin >> a[i];

    int step = 0;
    rep(i, n) {
        if (!a[i]) break;
        step++;
    }

    if (step&1) {
        puts("YES");
        return 0;
    }

    step = 0;
    for (int i = n-1; i >= 0; --i) {
        if (!a[i]) break;
        step++;
    }

    if (step&1) {
        puts("YES");
        return 0;
    }

    puts("NO");

    return 0;
}

例2： P1290 欧几里德的游戏

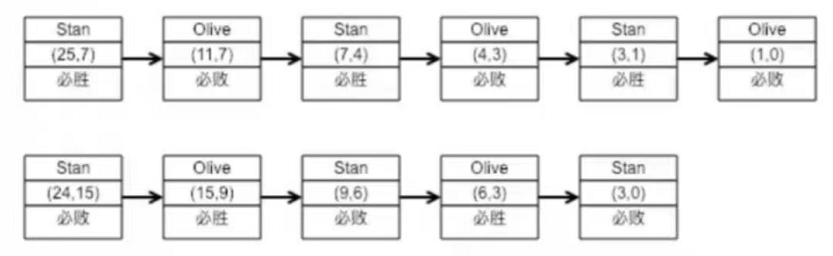
欧几里德的两个后代 Stan 和 Ollie 正在玩一种数字游戏，这个游戏是他们的祖先欧几里德发明的。给定两个正整数 $M$ 和 $N$，从 Stan 开始，从其中较大的一个数，减去较小的数的正整数倍，当然，得到的数不能小于 $0$。然后是 Ollie，对刚才得到的数，和 $M,N$ 中较小的那个数，再进行同样的操作 $\dots\dots$ 直到一个人得到了 $0$，他就取得了胜利。下面是他们用 $(25,7)$ 两个数游戏的过程：

Stan 赢得了游戏的胜利。

现在，假设他们完美地操作，谁会取得胜利呢？

分析：

分析一下 Stain 必胜和必败的游戏过程，每个长方形上方表示目前谁操作了。题目中说谁拿到 $0$ 谁胜利，其实可以理解成谁操作的时候面对 $0$ 就失败了。

第二种情况双方都没有什么变化空间，只能一路取到底，这时候由胜负奇偶数决定。
而第一种情况，开局的时候，Stan 可以选择到 $(11, 7)$ 或者 $(4, 7)$
对局过程中，存在 $a >= 2b$，先手必胜，因为在这种情况下，先手有了一次调节走到底的步数的奇偶的机会。

代码实现

#include <bits/stdc++.h>

using std::cin;
using std::cout;
using std::function;

int main() {
    int t;
    cin >> t;

    while (t--) {
        int m, n;
        cin >> m >> n;
        if (m < n) std::swap(m, n);
        bool ok = true;
        function<void(int, int)> gcd = [&](int a, int b) {
            if (a >= 2*b or a == b) {
                return;
            }
            ok = !ok;
            gcd(b, a%b);
        };
        gcd(m, n);
        if (ok) puts("Stan wins");
        else puts("Ollie wins");
    }

    return 0;
}

Ferguson 游戏

有两堆物品 $n, m > 0$ 在两个盒子里，要求轮流操作，将一个物品清空，将一个盒子的物品分到清空的那个中，使得两个盒子都不为空，当两个盒子中都只剩一个的时候结束。最终成功执行将两个盒子都剩一个的人获胜，问先手胜还是后手胜？

分析：唯一的终态 $(1, 1)$，状态为 $(m, n)$ 的人，先手必胜还是必败呢？按照 $k=m+n$ 的顺序，从小到大判断每个状态即可。下面的代码可以求出 $20$ 以内的状态的情况。

1 3
1 5
3 3
1 7
3 5
1 9
3 7
5 5
1 11
3 9
5 7
1 13
3 11
5 9
7 7
1 15
3 13
5 11
7 9
1 17
3 15
5 13
7 11
9 9

结论：$m, n$ 都为奇数，先手必败；$m,n$ 至少一个为偶数，先手胜

假设 $m, n$ 都是奇数，你先手的话，无论清除哪个，都会留下一个奇数。然后这个奇数分割只能分成一奇一偶（奇数没办法分成两个偶数），所以对手必定面对一奇一偶的情况，此时对手清除奇数，将偶数分为两个奇数，那么你就又面对两个奇数的局面。

所以 $m, n$ 都是奇数，你先手的话，对手可以找到一个策略，使你面对的永远是两个奇数，对手永远是一奇一偶。
而失败的条件就是，面对两个奇数。

同理，如果两个不全是奇数，你先手，就可以让对手永远处于奇数的局面。

策梅洛定理

定理表明在二人参与的游戏中，如果满足

• 游戏步骤有限
• 信息完备（可以理解为参与者知道所有与游戏相关的信息以及本次游戏中已发生所有步骤和结果）；
• 不会产生平局
• 确定性的（即运气因素并不牵涉在游戏中）

则或者先行一方有必胜策略，或者后行一方有必胜策略。

策梅洛定理的另一种表述是：在二人参与的游戏中，如果满足游戏步骤有限、信息完备、每一步骤都是确定性，则或者先行一方有必胜策略，或者先行一方有必和策略，或者后行一方有必胜策略。

Chomp! 游戏

有一个 $m \times n$ 棋盘，每次可以取走一个方格并拿掉它右边和上面的所有方格。拿到左下角的格子 $(1, 1)$ 的人输，给出 $m$ 和 $n$，问先手必胜还是必输。

结论：除去 $1 \times 1$ 大小的棋盘外，其他大小的棋盘，先手存在必胜策略。

假设棋盘大小为 $m \times n$。首先，游戏不可能产生平局。其次，由于每一步移动至少取走一个方格，因此不超过 $mn$ 步后游戏必定结束。由策梅洛定理，这个确定性二人有限信息完备，且不存在平局，则或者先行一方有必胜策略，或者后行一方有必胜策略。如果后手有必胜策略，使得无论先手第一次取哪个方格，后手都能获得最后的胜利。那么现在假设先手取最右上角的格子，接下来后手可以取 $(a, b)$ 使得自己进入必胜的局面。事实上，先手在第一次取的时候就可以取 $(a, b)$，之后完全模仿后手的必胜步骤，迫使后手失败。于是产生矛盾。因此不存在后手必胜策略，先手存在必胜策略。

注意：这个证明是非构造性证明，也即只是证明了先手必胜策略的存在性，但没有构造出具体必胜策略。虽然对于一些特殊的情况，比如棋盘是正方形、棋盘只有两行，可以找到必胜策略，但对于一般情况，还没有人能给具体给出 Chomp 的一般性必胜策略。

Nim游戏

最普遍的定义：有若干堆石子，每堆石子的数量都是有限的，每次每人进行一次移动。合法的移动要求：“选择一堆石子并拿走若干颗，且不能不拿”。当轮到某个人时所有的石子堆都已经被拿空了，则判为此人负，因为他此刻无法进行任何合法的移动。

为了方便阐述，以下列模型为例

用(a, b, c)表示这三堆物品各自的数目。

（1） 显然(0, 0, 0)是P局势，即为必败态，此时先手无可取的物品，必败。

（2） 而对于(n, n, 0)的局势，只要后手拿走和先手一样多的物品，最后必会形成局势(1)：(0, 0, 0)。即先手必败的P局势。故此也为P局势。

（3） 对于(n, m, 0)的局势，先手可以先拿走一些物品，使剩下的两堆物品相同即构成局势(2)：(n, n, 0)。

最终该模型的规律为：(a, b, c)为必败态当且仅当$a \ xor \ b \ xor \ c \ = 0$

证明

设p(a, b, c) = a xor b xor c
1）任何以$p(a, b, c)= 0$出发的局面(a, b, c')一定有$p(a, b, c’) \ne 0 $，否则可以得到c = c'
2）任何$p(a,b,c) \ne 0$的局面都可以走向$p(a,b,c)=0$的局面

对所有$p(a, b, c) = 0$的局面，不管先手如何走，一定会到达$p(a, b, c’) \ne 0$的局面。而后手一定可以通过选择一些物品走向$p(a’,b’,c’\’)$的局面，最终一定会走向$a=b=c$的P局势，因此对于$p(a, b, c) = 0$的局势，一定是P局势。

例如：p(4, 10, 14)=0

$4 = (0100)_2 = 0 + 4 + 0 + 0$
$10 = (1010)_2 = 8 + 0 + 2 + 0$
$14 = (1110)_2 = 8 + 4 + 2 + 0$

分解成二进制后，非零项成对出现。

所以有以下情况：
1. 先手拿掉$14$里的$8$和$2$，后手可以拿$10$里的$8$和$2$。最终剩下$4$和$4$，显然先手必输。
2. 先手拿掉$14$里的$4$，后手可以拿$4$里的$4$。则剩下$10$和$10$，显然先手必输。
3. 先手拿掉$14$里的$5$个，剩下$9$，即为$8+1$，则可以通过构造其他物品取走的数目满足成对出现。当前为$(4, 10, 9)$：

$4 = (0100)_2 = 0 + 4 + 0 + 0$
$10 = (1010)_2 = 8 + 0 + 2 + 0$
$9 = (1001)_2 = 8 + 0 + 0 + 1$

则，$4$中取走$1$个，为$(3, 10, 9)$：

$3 = (0011)_2 = 0 + 0 + 2 + 1$
$10 = (1010)_2 = 8 + 0 + 2 + 0$
$9 = (1001)_2 = 8 + 0 + 0 + 1$

如此，构造即可。

例题：【模板】nim 游戏

甲，乙两个人玩 $nim$ 取石子游戏。

$nim$ 游戏的规则是这样的：地上有 $n$ 堆石子（每堆石子数量小于 $10^4$），每人每次可从任意一堆石子里取出任意多枚石子扔掉，可以取完，不能不取。每次只能从一堆里取。最后没石子可取的人就输了。假如甲是先手，且告诉你这 $n$ 堆石子的数量，他想知道是否存在先手必胜的策略。

数据范围：$n \leqslant 10^4$

代码实现

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;

void solve() {
    int n;
    cin >> n;

    int ans = 0;
    rep(i, n) {
        int a;
        cin >> a;
        ans ^= a;
    }

    if (ans == 0) puts("No");
    else puts("Yes");
}

int main() {
    int t;
    cin >> t;

    while (t--) solve();

    return 0;
}

扩展：阶梯 Nim 游戏

模型： 在阶梯上进行，每层有若干个石子，每次可以选择任意层的任意个石子将其移动到该层的下一层。最后不能操作的人输。

结论： 奇数阶梯上的石子异或起来，若是 $0$ 就先手必败，否则先手必胜。

证明： 阶梯博弈经过转换可以变为 Nim，把所有奇数阶梯看成 $N$ 堆石子做 $nim$。
把石子从奇数堆移动到偶数堆可以理解为拿走石子，就相当于几个奇数堆的石子在做 $nim$。

组合游戏的和

• 假设有 $k$ 个组合游戏 $G_1, G_2, \cdots, G_k$，可以定义一个新游戏，在每个回合中，当前游戏可以任选一个子游戏进行合法操作，而让其他游戏的局面保持不变，不能操作的游戏者输。这个游戏称为 $G_1, G_2, \cdots, G_n$ 的和
• 前面的 $n$ 堆石子的 $nim$ 游戏，就可以看成是 $n$ 个单堆石子 $nim$ 游戏的和

SG 函数

首先定义 mex(minimal excludant) 运算，这是施加于一个集合的运算，表示最小的不属于这个集合的非负整数。例如，$mex\{0, 1, 2, 4\} = 3$，$mex\{2, 3, 5\} = 0$，$mex\{\} = 0$。

对于一个给定的有向无环图，定义关于图的每个顶点的 $SG$ 函数如下：sg(x) = mex{sg(y) | y 是 x 的后继}
也就是说，一个点的 $SG$ 函数为在它所在后继中都未出现的最小的值。

来看一下 $SG$ 函数的性质。首先，所有的没有出边的顶点，其 $SG$ 值为 $0$，因为它的后继集合为空集。然后对于一个 $sg(x) = 0$ 的点 $x$，它的所有后继 $y$ 都满足 $sg(x) \neq 0$。对于一个 $sg(x) \neq 0$ 的点，必定存在一个后继 $y$ 满足 $sg(y) = 0$

顶点 $x$ 所代表的状态是 $P$ 状态（必败）当且仅当 $sg(x) = 0$
顶点 $x$ 所代表的状态是 $N$ 状态（必胜）当且仅当 $sg(x) \neq 0$

取石子问题，有 $1$ 堆 $n$ 个的石子，每次只能取 $\{1, 3, 4\}$ 个石子，先取完石子者胜利，那么各个值的 $SG$ 值为多少？

$sg[0] = 0, f[] = \{1, 3, 4\}$

$x = 1$ 时，可以取走 $1 - f\{1\}$ 个石子，剩余 $\{0\}$ 个，$mex\{sg[0]\} = mex\{0\}$，故 $sg[1] = 1$

$x = 2$ 时，可以取走 $2 - f\{1\}$ 个石子，剩余 $\{1\}$ 个，$mex\{sg[1]\} = mex\{1\}$，故 $sg[2] = 0$

$x = 3$ 时，可以取走 $3 - f\{1, 3\}$ 个石子，剩余 $\{2, 0\}$ 个，$mex\{sg[2], sg[0]\} = mex\{0, 0\}$，故 $sg[3] = 1$

$x = 4$ 时，可以取走 $4 - f\{1, 3, 4\}$ 个石子，剩余 $\{3, 1, 0\}$，$mex\{sg[3], sg[1], sg[0]\} = mex\{1, 1, 0\}$，故 $sg[4] = 2$

$x = 5$ 时，可以取走 $5 - f\{1, 3, 4\}$ 个石子，剩余 $\{4, 2, 1\}$，$mex\{sg[4], sg[2], sg[1]\} = mex\{2, 0, 1\}$，故 $sg[5] = 3$

SG 定理

对于任意 $G = G_1 + G_2 + \cdots + G_n$
有 $sg(G) = sg(G_1) \oplus sg(G_2) \oplus \cdots \oplus sg(G_n)$
游戏和的 $SG$ 函数等于各个子游戏 $SG$ 函数的异或和

$nim$ 问题可以看成 $SG$ 定理的直接应用，因为单堆石子的 $SG$ 函数 $SG(x) = x$

0   sg(0) = 0
1   mex{sg(0)} = 1
2   mex{sg(1), sg(0)} = mex{1, 0} = 2
...
x   sg(x) = x

解决游戏的和的问题，可以分别计算每个子问题，再取异或和

例题：E&D