基本定义

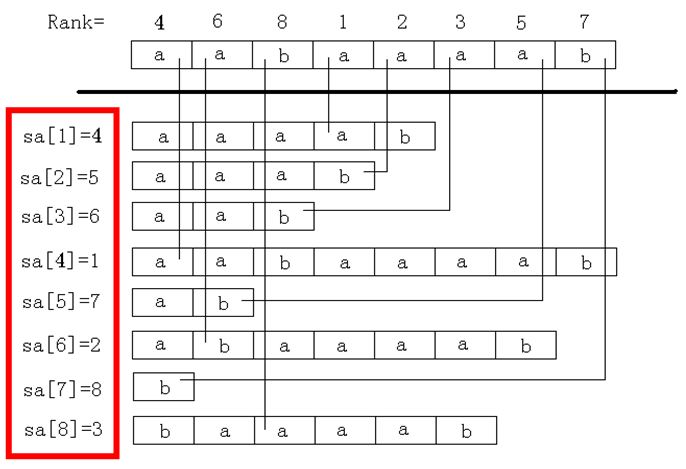
后缀数组：后缀数组SA保存1...n的一个排列, 并且Suffix(SA[i])<Suffix(SA[i + 1]), 即SA表示
排第i名的后缀是谁.

名次数组：名次数组Rank[i]保存的是Suffix(i)在所有后缀中从小到大排列的”名次”.

为了叙述方便，以第k个字符开始的后缀称为后缀k。

以字符串“aabaaaab”为例。

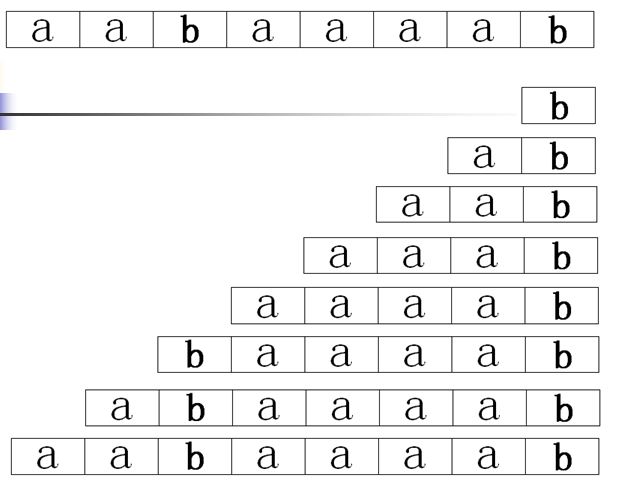
设字符串的长度为n. 为了方便比较大小, 可以在字符串后面增加一个字符, 这个字符比前面的字符都要小.

后缀数组求解的方法

• 倍增算法O(nlogn)
• $DC3$算法O(n)
• $DC3$算法实现起来麻烦一些且常数较大, 这里主要讲倍增算法

倍增算法

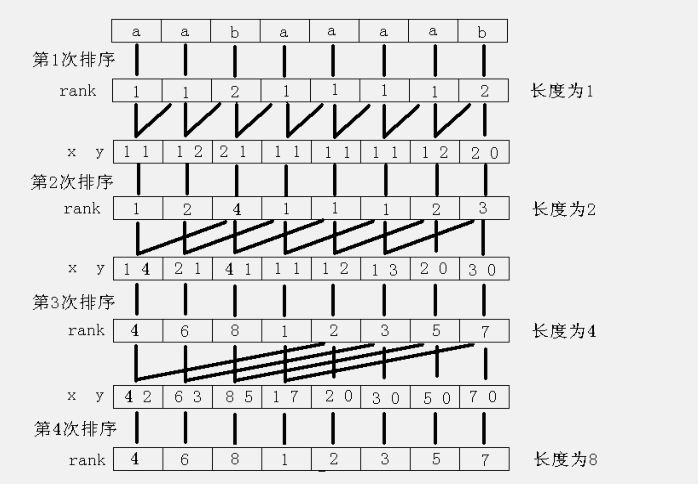
倍增算法的主要思路: 用倍增的方法对每个字符开始的长度为$2^k$的子字符串进行排序, 求出排名, 即rank值. k从0开始, 每次加1, 当$2^k$大于n以后, 每个字符开始的长度为$2^k$的子字符串便相当于所有的后缀.并且这些子字符串都一定已经比较出大小, 即rank值中没有相同的值, 那么此时的rank值就是最后的结果. 每一次排序都利用上次长度为$2^{k-1}$的字符串的rank值, 那么长度为$2^k$的字符串可以用两个长度为$2^{k-1}$的字符串的排名关系作为value来基数排序.

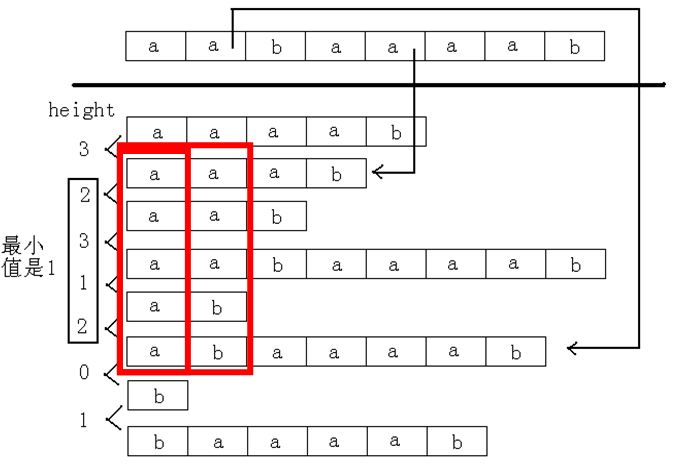
height数组

height数组: 定义height[i] = LCP(suffix(sa[i - 1]),suffix(sa[i])). 对于j和k, 不妨设rank[j] < rank[k], 则
LCP(j, k) = min{hight[rank[j] + 1], hight[rank[j] +2], ... ,hight[rank[k]]}

• 例如，字符串为“aabaaaab”，求后缀“abaaaab”和后缀“aaab”的最长公共前缀。

height数组求法

暴力求解hight数组的时间复杂度会达到O(n^2)
• 下面来看一下时间复杂度较低的做法.
• 设h[i] = height[rank[i]], h数组有这样的一个性质:
• h[i]>=h[i - 1]-1
• 证明：
设suffix(k)是排在suffix(i-1)前一名的后缀, 则他们的最长公共前缀是h[i-1]。那么suffix(k+1)将排在suffix(i)前面,并且suffix(k+1)和suffix(i)的最长公共前缀是h[i - 1] - 1, 所以suffix(i)和在它前一名的后缀的最长公共前缀至少是h[i- 1] - 1.

代码实现

char ch[MAXN], All[MAXN];
int SA[MAXN], rank[MAXN], Height[MAXN], tax[MAXN], a[MAXN], n, m;
char str[MAXN];
// rank[i] 第i个后缀的排名，SA[i]排名为i的后缀位置，Height[i]排名为i的后缀与排名为(i-1)的后缀的LCP
// tax[i] 基数排序辅助数组；tp[i] rank的辅助数组（基数排序中的第二关键字），与SA意义一样
// a为原串
void RSort() {
    // rank第一关键字，tp第二关键字
    for (int i = 0; i <= m; ++i) tax[i] = 0;
    for (int i = 1; i <= n; ++i) tax[rank[tp[i]]]++;
    for (int i = 1; i <= m; ++i) tax[i] += tax[i - 1];
    for (int i = n; i >= 1; --i) SA[tax[rank[tp[j]]]--] = tp[i]; // 确保满足第一关键字的同时，再满足第二关键字的要求 
} // 基数排序，把新的二元组排序

// 通过二元组两个下标的比较，确定两个子串是否相同 
int cmp(int *f, int x, int y, int w) {
    return f[x] == f[y] && f[x + w] == f[y + w];
}

void Suffix() {
    // SA
    for (int i = 1; i <= n; ++i) rank[i] = a[i], tp[i] = i;
    m = 127, RSort(); // 一开始是以单个字符为单位，所以m = 127

    for (int w = 1, p = 1, i; p < n; w += w, m = p) { // 把子串长度翻倍，更新rank 
        // w当前一个子串的长度，m当前离散后的排名种类数
        // 当前的tp（第二关键字）可直接由上一次的SA得到
        for (int p = 0, i = n - w + 1; i <= n; ++i) tp[++p] = i; // 长度越界，第二关键字为0
        for (i = 1; i <= n; ++i) if (SA[i] > w) tp[++p] = SA[i] - w;

         // 用已经完成的SA来更新与它互逆的rank，并离散rank
         for (i = 2; i <= n; ++i) rank[SA[i]] = cmp(tp, SA[i], SA[i - 1], w) ?  p : ++p;
    } 

    // 离散，把相等的字符串的rank设为相同
    // LCP
    int j, k = 0;
    for (int i = 1; i <= n; Height[rank[i++]] = k) 
        for (k = k ? k - 1 : k, j = SA[i - 1]; a[i + k] == a[j + k]; ++k);
    // 这个知道原理后比较好理解程序 
}