动态开点线段树
用处:一般线段树开局直接4*N的空间，然而当N很大时，4倍空间会消耗很多，这时考虑用动态开点线段树，用多少开多少，跟c++的new差不多

预备：一个根节点root,存值数组c[N],左右儿子 lc[N],rc[N]

算法流程：
1.一开始只有一个根节点
2.update操作:类似串算法，每次传入节点root,区间范围[l,r]和更新点x,判断x在区间的哪边，在哪边就就往哪边走，如果遇到一个无标记的节点但又需要往这个节点走
就以访问次序给这个节点标号，像正常线段树更新即可。
3.query操作:和一般线段树不同的是，当我们遇到一个没有访问过的节点，直接返回，其他与线段树查询一致。

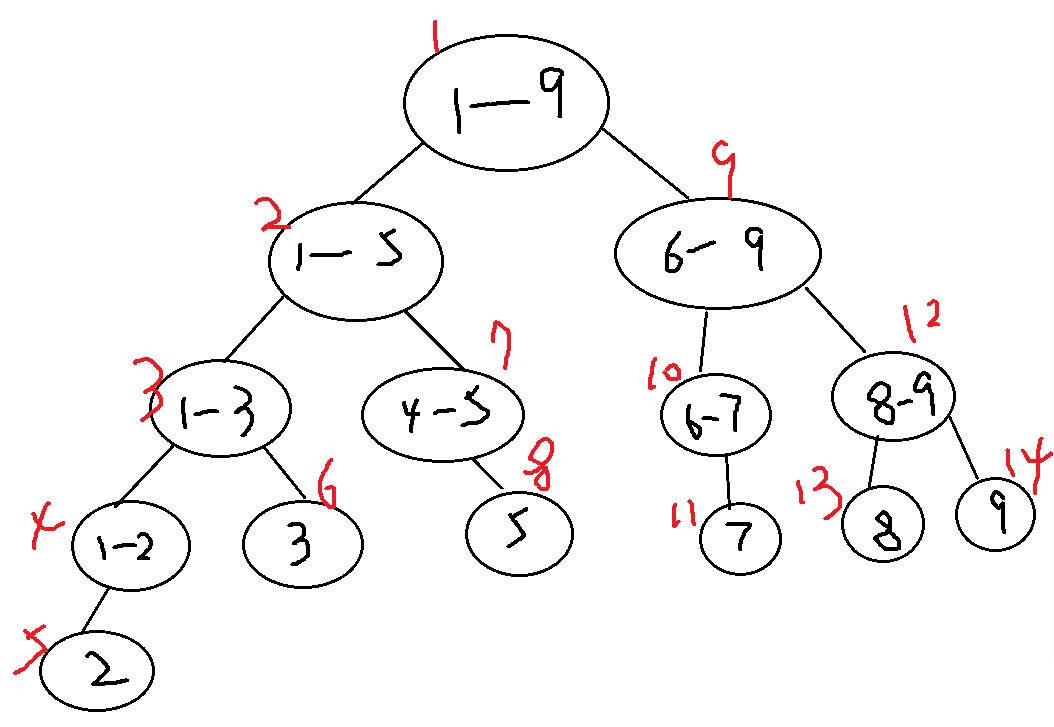
假设我们要对 1 3 5 7 8 9这段序列操作，区间范围[1,9] 开的线段树如下可以少点2,4,6这3个儿子节点
如果这段区间没有5，我们甚至可以不用开7号和8号节点

下面以求逆序对为例用

#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

const int N=1e7+7;

int root,n,c[N],lc[N],rc[N],cnt;

void update(int &p,int l,int r,int x,int val)
{
    if(!p) p=++cnt; //遇到了，但没标号，标记
    if(l==r)
    {
        c[p]+=val;
        return;
    }
    int mid=(l+r)>>1;
    if(x<=mid) update(lc[p],l,mid,x,val);
    else update(rc[p],mid+1,r,x,val);
    c[p]=c[lc[p]]+c[rc[p]];
}

int query(int p,int l,int r,int x,int y)
{
     if(!p) return 0;
     if(l==x&&r==y) return c[p];
     int mid=(l+r)>>1;
     if(y<=mid) return query(lc[p],l,mid,x,y);
     else if(x>mid) return query(rc[p],mid+1,r,x,y);
     return query(lc[p],l,mid,x,mid)+query(rc[p],mid+1,r,mid+1,y);
}
int main()
{
    ios::sync_with_stdio(false);
    cin>>n;
    long long ans=0;
    for(int i=1;i<=n;i++)
    {
        int x;
        cin>>x;
        ans+=query(root,1,1e9,x+1,1e9);
        update(root,1,1e9,x,1);
    }
    cout<<ans<<endl;
    return 0;
}