终于写完13题的题解了
用时 $23$ 天
以此帖纪念洛谷红名
题单:
$$\Huge \color{red}{题单}$$
- P2568 GCD
- P2398 GCD SUM
- P1447 [NOI2010] 能量采集
- P2522 [HAOI2011]Problem b
- P4318 完全平方数
- P2257 YY的GCD
- P1829 [国家集训队]Crash的数字表格 / JZPTAB
- P3327 [SDOI2015]约数个数和
- P4449 于神之怒加强版
- P3312 [SDOI2014]数表
- P3704 [SDOI2017]数字表格
- CF1780F Three Chairs
- CF235E Number Challenge
T1 P2568 GCD
题目描述
给定正整数 $n$,求 $1\le x,y\le n$ 且 $\gcd(x,y)$ 为素数的数对 $(x,y)$ 有多少对。
题目简化:求 $\sum_{p \in primes} \sum_{i=1}^{n} \sum_{j=1}^{n} [\gcd(i, j) == p]$
转化为 $\sum_{p \in primes} \sum_{i=1}^{\lfloor \frac{n}{p} \rfloor} \sum_{j=1}^{\lfloor \frac{n}{p} \rfloor} [\gcd(i, j) == 1]$
$ans = \sum_{i=1}^{\lfloor \frac{n}{p} \rfloor} \phi(i)$
#include <bits/stdc++.h>
using namespace std;
const long long N = 1e7 + 10;
long long euler[N], primes[N], sum[N], cnt;
bool st[N];
long long n;
void get_eulers(long long n) // 线性筛法求1~n的欧拉函数
{
euler[1] = 1;
for (long long i = 2; i <= n; i ++ ) {
if (!st[i]) {
primes[ ++cnt ] = i;
euler[i] = i - 1;
}
for (long long j = 1; primes[j] <= n / i; j ++ ) {
long long t = primes[j] * i;
st[t] = true;
if (i % primes[j] == 0) {
euler[t] = euler[i] * primes[j];
break;
}
euler[t] = euler[i] * (primes[j] - 1);
}
}
}
int main() {
scanf("%d", &n);
get_eulers(n);
for (long long i = 1; i <= n; i++) sum[i] = sum[i - 1] + euler[i];
long long ans = 0;
for (long long i = 1; i <= cnt && primes[i] <= n; i++) ans += 1ll * (sum[n / primes[i]] * 2) - 1;
cout << ans;
return 0;
}
T2 P2398 GCD SUM
题目描述
求
$$\sum_{i=1}^n \sum_{j=1}^n \gcd(i, j)$$
从 $\gcd$ 入手。
设 $f_k$ 为 $\gcd(i,j) == k$ 的个数。
则 $ans = \sum_{i=1}^{n} f_i \times i$
但这样不好算,因此引入 $g$ 数组。
设 $g_k$ 为 $k | gcd(i,j)$ 的个数。
由 $g$ 的定义,$g_k = \lfloor \frac{n}{k} \rfloor ^ 2$
这两个 $g_k$ 相等,因此可以这么表示 $f_k$:
$f_k = \lfloor \frac{n}{k} \rfloor ^ 2 - f_{2k} - f{3k} - ......$
求 $f$ 数组方便多了,可以逆序推导 $f$,最后统计答案。
#include <bits/stdc++.h>
using namespace std;
const long long N = 1e5 + 10;
long long n, f[N];
long long ans = 0;
int main() {
scanf("%d", &n);
for (long long i = n; i > 0; i--) {
long long x = i; f[i] = (n / i) * (n / i);
while (x + i <= n) {
x += i;
f[i] -= f[x];
}
ans += f[i] * i;
}
cout << ans;
return 0;
}
T3 P1447 [NOI2010] 能量采集
题目描述
栋栋有一块长方形的地,他在地上种了一种能量植物,这种植物可以采集太阳光的能量。在这些植物采集能量后,栋栋再使用一个能量汇集机器把这些植物采集到的能量汇集到一起。
栋栋的植物种得非常整齐,一共有 $n$ 列,每列有 $m$ 棵,植物的横竖间距都一样,因此对于每一棵植物,栋栋可以用一个坐标 $(x, y)$ 来表示,其中 $x$ 的范围是 $1$ 至 $n$,$y$ 的范围是 $1$ 至 $m$,表示是在第 $x$ 列的第 $y$ 棵。
由于能量汇集机器较大,不便移动,栋栋将它放在了一个角上,坐标正好是 $(0, 0)$。
能量汇集机器在汇集的过程中有一定的能量损失。如果一棵植物与能量汇集机器连接而成的线段上有 $k$ 棵植物,则能量的损失为 $2k + 1$。例如,当能量汇集机器收集坐标为 $(2, 4)$ 的植物时,由于连接线段上存在一棵植物 $(1, 2)$,会产生 $3$ 的能量损失。注意,如果一棵植物与能量汇集机器连接的线段上没有植物,则能量损失为 $1$。现在要计算总的能量损失。
下面给出了一个能量采集的例子,其中 $n = 5$,$m = 4$,一共有 $20$ 棵植物,在每棵植物上标明了能量汇集机器收集它的能量时产生的能量损失。
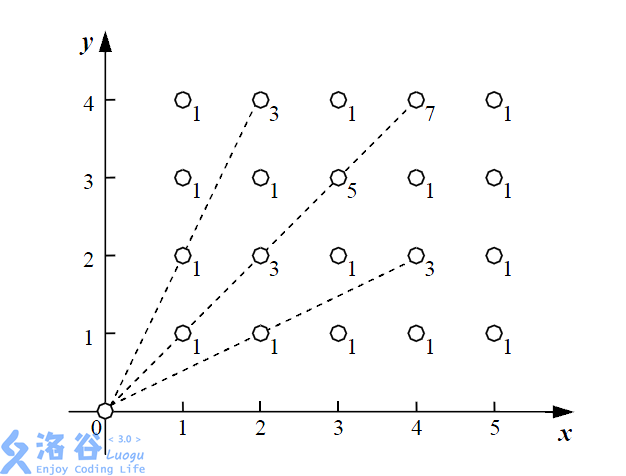
在这个例子中,总共产生了 $36$ 的能量损失。
题意转化:求
$\bigg( 2 \times \sum_{i=1}^{n} \sum_{j=1}^{m} \gcd(i,j) \bigg) - n \times m$。
引理:欧拉反演。
$$n = \sum_{d|n} \phi(d)$$
现在重点只考虑 $\sum_{i=1}^{n} \sum_{j=1}^{m} \gcd(i,j)$。
转化为:$\sum_{i=1}^{n} \sum_{j=1}^{m} \sum_{d|gcd(i,j)} \phi(d)$。
$=\sum_{d=1}^{n} \phi(d) \sum_{i=1}^{n} \sum_{j=1}^{m} [d|gcd(i,j)]$
$=\sum_{d=1}^{n} \phi(d) \lfloor \frac{n}{d} \rfloor \lfloor \frac{m}{d} \rfloor$
直接线性筛 $\phi$ 就行了。
#include <bits/stdc++.h>
using namespace std;
const long long N = 1e7 + 10;
long long euler[N], primes[N], sum[N], cnt;
bool st[N];
long long n, m;
void get_eulers(long long n) // 线性筛法求1~n的欧拉函数
{
euler[1] = 1;
for (long long i = 2; i <= n; i ++ ) {
if (!st[i]) {
primes[ ++cnt ] = i;
euler[i] = i - 1;
}
for (long long j = 1; primes[j] <= n / i; j ++ ) {
long long t = primes[j] * i;
st[t] = true;
if (i % primes[j] == 0) {
euler[t] = euler[i] * primes[j];
break;
}
euler[t] = euler[i] * (primes[j] - 1);
}
}
}
int main() {
scanf("%d%d", &n, &m);
get_eulers(n);
for (long long i = 1; i <= n; i++) sum[i] = sum[i - 1] + euler[i];
long long ans = 0;
for (int d = 1; d <= n; d++) {
ans += euler[d] * (n / d) * (m / d);
}
cout << 2 * ans - n * m;
return 0;
}
T4 P2522 [HAOI2011]Problem b
题目描述
对于给出的 $n$ 个询问,每次求有多少个数对 $(x,y)$,满足 $a \le x \le b$,$c \le y \le d$,且 $\gcd(x,y) = k$,$\gcd(x,y)$ 函数为 $x$ 和 $y$ 的最大公约数。
简化题意:求
$$\sum_{i=a}^{b} \sum_{j=c}^{d} [\gcd(i,j) == k]$$
这题有一个类似二维前缀和的思想,或者说是容斥。
$Ans = solve((1,b),(1,d))-solve((1,b),(1,c-1))-solve((1,a-1),(1,d))+solve((1,a-1),(1,c-1))$
至此,完成了 $1-n,1-m$的转化。只要求解这个子问题就行了。
P3455 [POI2007]ZAP-Queries
这题即是 T4 的子问题。
题目描述
密码学家正在尝试破解一种叫 BSA 的密码。
他发现,在破解一条消息的同时,他还需要回答这样一种问题:
给出 $a,b,d$,求满足 $1 \leq x \leq a$,$1 \leq y \leq b$,且 $\gcd(x,y)=d$ 的二元组 $(x,y)$ 的数量。
因为要解决的问题实在太多了,他便过来寻求你的帮助。
设 $f(k) = \sum_{i=1}^{a} \sum_{i=1}^{b} [\gcd(i,j)==k]$
设 $g(k) = \sum_{n|k} f(k) = \lfloor \frac{a}{n} \rfloor \lfloor \frac{b}{n} \rfloor$
根据莫反有:$f(k) = \sum_{n|k} \mu(\lfloor \frac{k}{n} \rfloor) F(k)$
根据题目,$Ans = f(d)$。
把 $Ans$ 用莫反的式子表示出来:
$Ans = \sum_{d|k} \mu(\lfloor \frac{k}{d} \rfloor) F(k)$
$Ans = \sum_{d|k} \mu(\lfloor \frac{k}{d} \rfloor) \lfloor \frac{a}{k} \rfloor \lfloor \frac{b}{k} \rfloor$
设 $t=\frac{b}{k}$,改为枚举 $t$,则:
$Ans = \sum_{t=1}^{\min(\lfloor \frac{a}{d} \rfloor , \lfloor \frac{b}{d} \rfloor)} \mu(t) \lfloor \frac{a}{td} \rfloor \lfloor \frac{b}{td} \rfloor$
至此,该子问题得到了解决,已经是 $O(N)$ 的效率了。
但是由于多组数据,需要采用数论分块优化到 $O(\sqrt N)$。
子问题代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int mu[N], prime[N], tot = 0, sum[N];
bool st[N];
int read(){
int x = 0; int zf = 1; char ch = ' ';
while (ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
if (ch == '-') zf = -1, ch = getchar();
while (ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar(); return x * zf;
}
inline void init(int n) {
mu[1] = 1;
for (register int i = 2; i <= n; i++) {
if (!st[i]) prime[++tot] = i, mu[i] = -1;
for (register int j = 1; j <= tot && prime[j] * i <= n; j++) {
st[prime[j] * i] = 1;
if (i % prime[j] != 0) mu[i * prime[j]] = -mu[i];
else { mu[prime[j] * i] = 0; break; }
}
}
for (int i = 1; i <= n; i++) sum[i] = sum[i - 1] + mu[i];
}
int k;
int f(int x, int y) {
int res = 0;
for (int l = 1, r; l <= min(x, y); l = r + 1) {
r = min(x / (x / l), y / (y / l));
res += (sum[r] - sum[l - 1]) * ((x / k) / l) * ((y / k) / l);
}
return res;
}
int main() {
init(50000);
int T; T = read();
while (T--) {
static int a, b; a = read(), b = read(), k = read();
printf("%lld\n", f(a, b));
}
return 0;
}
原问题只需要像开头说的一样容斥解决。
代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int mu[N], prime[N], tot = 0, sum[N];
bool st[N];
int read(){
int x = 0; int zf = 1; char ch = ' ';
while (ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
if (ch == '-') zf = -1, ch = getchar();
while (ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar(); return x * zf;
}
inline void init(int n) {
mu[1] = 1;
for (register int i = 2; i <= n; i++) {
if (!st[i]) prime[++tot] = i, mu[i] = -1;
for (register int j = 1; j <= tot && prime[j] * i <= n; j++) {
st[prime[j] * i] = 1;
if (i % prime[j] != 0) mu[i * prime[j]] = -mu[i];
else { mu[prime[j] * i] = 0; break; }
}
}
for (int i = 1; i <= n; i++) sum[i] = sum[i - 1] + mu[i];
}
int k;
int f(int x, int y) {
int res = 0;
for (int l = 1, r; l <= min(x, y); l = r + 1) {
r = min(x / (x / l), y / (y / l));
res += (sum[r] - sum[l - 1]) * ((x / k) / l) * ((y / k) / l);
}
return res;
}
int main() {
init(50000);
int T; T = read();
while (T--) {
static int a, b, c, d; a = read(), b = read(), c = read(), d = read(), k = read();
printf("%lld\n", f(b, d) - f(b, c - 1) - f(a - 1, d) + f(a - 1, c - 1));
}
return 0;
}
T5 P4318 完全平方数
题目描述
小 X 自幼就很喜欢数。但奇怪的是,他十分讨厌完全平方数。他觉得这些数看起来很令人难受。由此,他也讨厌所有是完全平方数的正整数倍的数。然而这丝毫不影响他对其他数的热爱。
这天是小X的生日,小 W 想送一个数给他作为生日礼物。当然他不能送一个小X讨厌的数。他列出了所有小X不讨厌的数,然后选取了第 K个数送给了小X。小X很开心地收下了。
然而现在小 W 却记不起送给小X的是哪个数了。你能帮他一下吗?
题意简化:
多组数据,每次求第 $K$ 个不含大于 $1$ 的完全平方因子的正整数。
由于当时正好学杜教筛,因此就用了杜教筛的方法。
详见 OI-Wiki
杜教筛可以在低于线性时间内处理数论函数的前缀和。
个人认为就是个记忆化+预处理优化。
回到原题,平方因子和莫比乌斯函数有点关系。
题目要求第 $K$ 个满足条件的数,因此有:$\sum_{i=1}^{ans} [\mu(i) \neq 0] == K$,并且 $\mu(ans) \neq 0$。
$\mu$ 函数有三种取值:$-1,0,1$。$-1$ 不是很好处理,要特判,因此直接用 $\mu^2(n)$ 来代替 $\mu(n)$。(并不代表这两个等价,只是在此题中用此方法更方便)
设 $f(n) = \mu^2(n), S(n) = \sum_{i=1}^{n} f(i)$
因此 $S(ans) == k$ 且 $f(ans) \neq 0$。
杜教筛可以在低于线性时间内处理数论函数的前缀和。
数据范围已经高到 $10^9$ 了,而且要处理前缀和的 $\mu^2$ 是一个积性函数。
因此考虑杜教筛。
这里设 $g(n) = [n = k^2, k \in N_{+}]$。
再考虑卷积:$(f \times g)(n) = \sum_{d | n} {g(d) \times f( \frac{n}{d} )}$
这里 $g(d) \times f( \frac{n}{d} )$ 只有在 $d$ 取 $n$ 的最大平方因子时为 $1$,否则为 $0$。
它的前缀和是很好求的,因为每个数都有最大平方因子(每个数都是 $1$ 的倍数)。因此 $(f \times g)(n) = 1(n) = 1$。
继续往后推:$g(1)S(n) = \sum_{i=1}^{n} (f \times g)(i) - \sum_{i=2}^{n} g(i) \times S(\lfloor \frac{n}{i} \rfloor) = n - \sum_{i=2}^{n} g(i) \times S(\lfloor \frac{n}{i} \rfloor)$
把 $g$ 函数去掉,即枚举平方因子:
$S(n) = n - \sum_{i=2}^{n} g(i) \times S(\lfloor \frac{n}{i} \rfloor) = n - \sum_{i=2}^{\sqrt n} S(\lfloor \frac{n}{i^2} \rfloor)$
到这里就可以直接杜教筛了。
#include <bits/stdc++.h>
using namespace std;
const int N = 1005010;
int mu[N], prime[N], sum[N], tot = 0;
bool st[N];
inline void init(int n) {
sum[1] = mu[1] = 1;
for (register long long i = 2; i <= n; i++) {
if (!st[i]) prime[++tot] = i, mu[i] = 1;
for (register int j = 1; j <= tot && prime[j] * i <= n; j++) {
st[prime[j] * i] = 1;
if (i % prime[j] != 0) mu[i * prime[j]] = mu[i];
else { mu[prime[j] * i] = 0; break; }
}
sum[i] = sum[i - 1] + mu[i];
}
}
int T, n;
map<int, int> mp;
int dfs(int x) {
if (x <= N - 3) return sum[x];
if (mp[x]) return mp[x];
int ans = x;
for (int i = 2; i * i <= x; i++) ans -= dfs(x / (i * i));
mp[x] = ans;
return ans;
}
int main() {
init(N - 3);
scanf("%d", &T);
while (T--) {
scanf("%d", &n);
long long l = n, r = 2 * n;
while (l < r) {
long long mid = l + r >> 1;
if (dfs(mid) >= n) r = mid;
else l = mid + 1;
}
printf("%lld\n", r);
}
return 0;
}
T6 P2257 YY的GCD
题目描述
神犇 YY 虐完数论后给傻× kAc 出了一题
给定 $N, M$,求 $1 \leq x \leq N$,$1 \leq y \leq M$ 且 $\gcd(x, y)$ 为质数的 $(x, y)$ 有多少对。
简化题意:求 $\sum_{i=1}^{N} \sum_{j=1}^{M} [\gcd(i,j) \in Prime]$
提出 $p$:
$\sum_{p \in Prime} \sum_{i=1}^{N} \sum_{j=1}^{M} [\gcd(i,j) == p]$
套路:
$\sum_{p \in Prime} \sum_{i=1}^{\lfloor \frac{N}{p} \rfloor} \sum_{j=1}^{\lfloor \frac{M}{p} \rfloor} [\gcd(i,j) == 1]$
$\sum_{p \in Prime} \sum_{i=1}^{\lfloor \frac{N}{p} \rfloor} \sum_{j=1}^{\lfloor \frac{M}{p} \rfloor} [\gcd(i,j) == 1]$
$\sum_{p \in Prime} \sum_{i=1}^{\lfloor \frac{N}{p} \rfloor} \sum_{j=1}^{\lfloor \frac{M}{p} \rfloor} \sum_{d|i,d|j} \mu(d)$
$\sum_{p \in Prime} \sum_{d=1}^{\frac{\min(N,M)}{p}} \mu(d) \times \lfloor \frac{N}{pd} \rfloor \lfloor \frac{M}{pd} \rfloor$
设 $t=pd$
$\sum_{p \in Prime} \sum_{d=1}^{\frac{\min(N,M)}{p}} \mu(d) \times \lfloor \frac{N}{t} \rfloor \lfloor \frac{M}{t} \rfloor$
$\sum_{t=1}^{\min(N,M)} \lfloor \frac{N}{t} \rfloor \lfloor \frac{M}{t} \rfloor \sum_{d \in Prime, d | t} \mu(\frac{t}{d})$
套路一下,设 $F(x)=\sum_{d \in Prime, d | x} \mu(\frac{x}{d})$
接下来前面部分数论分块就好了。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e7 + 10;
int mu[N], prime[N], tot = 0, f[N];
bool st[N];
void init(int n) {
mu[1] = 1;
for (int i = 2; i <= n; i++) {
if (!st[i]) prime[++tot] = i, mu[i] = -1;
for (int j = 1; j <= tot && prime[j] * i <= n; j++) {
st[prime[j] * i] = 1;
if (i % prime[j] != 0) mu[i * prime[j]] = -mu[i];
else { mu[prime[j] * i] = 0; break; }
}
}
for (int i = 1; i <= tot; i++)
for (int j = prime[i]; j <= n; j += prime[i]) f[j] += mu[j / prime[i]];
for (int i = 1; i <= n; i++) f[i] += f[i - 1];
}
int main() {
init(1e7);
int T, n, m, nn;
scanf("%d", &T);
while (T--) {
scanf("%d%d", &n, &m); nn = min(n, m);
long long ans = 0, l = 0, r = 0;
for (int i = 1; i <= nn;) {
l = i; long long x = n / l, y = m / l;
r = min(n / x, m / y);
ans += 1ll * x * 1ll * y * 1ll * (f[r] - f[l - 1]);
i = r + 1;
}
cout << ans << endl;
}
return 0;
}
T7 P1829 【国家集训队】Crash的数字表格 / JZPTAB
题目描述
今天的数学课上,Crash 小朋友学习了最小公倍数(Least Common Multiple)。对于两个正整数 $a$ 和 $b$,$\text{lcm}(a,b)$ 表示能同时整除 $a$ 和 $b$ 的最小正整数。例如,$\text{lcm}(6, 8) = 24$。
回到家后,Crash 还在想着课上学的东西,为了研究最小公倍数,他画了一张 $ n \times m$ 的表格。每个格子里写了一个数字,其中第 $i$ 行第 $j$ 列的那个格子里写着数为 $\text{lcm}(i, j)$。
看着这个表格,Crash 想到了很多可以思考的问题。不过他最想解决的问题却是一个十分简单的问题:这个表格中所有数的和是多少。当 $n$ 和 $m$ 很大时,Crash 就束手无策了,因此他找到了聪明的你用程序帮他解决这个问题。由于最终结果可能会很大,Crash 只想知道表格里所有数的和 $\bmod 20101009$ 的值。
题目简化:求 $\sum_{i=1}^{n} \sum_{j=1}^{m} lcm(i,j)$
即 $\sum_{i=1}^{n} \sum_{j=1}^{m} \frac{i \times j}{\gcd(i,j)}$
$\sum_{d=1}^{\min(n,m)} \sum_{i=1}^{n} \sum_{j=1}^{m} \frac{i \times j}{d} [\gcd(i,j) == d]$
$\sum_{d=1}^{\min(n,m)} d \sum_{i=1}^{\lfloor \frac{n}{d} \rfloor} \sum_{j=1}^{\lfloor \frac{m}{d} \rfloor} i \times j \times [\gcd(i,j) == 1]$
考虑后面部分:
$s(n,m)=\sum_{i=1}^{n} \sum_{j=1}^{m} i \times j \times [\gcd(i,j) == 1]$
$s(n,m)=\sum_{d=1}^{\min(n,m)} \mu(d) \times \sum_{d|i}^{n} \sum_{d|j}^{m} i \times j$
$s(n,m)=\sum_{d=1}^{\min(n,m)} \mu(d) \times d^2 \times \sum_{i=1}^{\lfloor \frac{n}{d} \rfloor} \sum_{j=1}^{\lfloor \frac{m}{d} \rfloor} i \times j$
这个柿子前半部分可以直接前缀和,后半部分可以公式计算:
设 $sum(n,m)=\sum_{i=1}^{n} \sum_{j=1}^{m} i \times j = \frac{n \times (n + 1)}{2} \times \frac{m \times (m + 1)}{2}$
则代入原来的式子:
$s(n,m)=\sum_{d=1}^{\min(n,m)} \mu(d) \times d^2 \times sum(\lfloor \frac{n}{d} \rfloor , \lfloor \frac{m}{d} \rfloor)$
至此,$s$ 函数可以用数论分块解决了。
带回原式:
$Ans = \sum_{d=1}^{n} d \times s(\lfloor \frac{n}{d} \rfloor, \lfloor \frac{m}{d} \rfloor)$
这个式子也可以数论分块!
因此这道题双重数论分块即可解决。
#include <bits/stdc++.h>
using namespace std;
const long long N = 1e7 + 10, mod = 20101009;
long long mu[N], prime[N], sum[N], tot;
bool st[N];
inline void init(long long n) {
mu[1] = 1;
for (register long long i = 2; i <= n; i++) {
if (!st[i]) prime[++tot] = i, mu[i] = -1;
for (register long long j = 1; j <= tot && prime[j] * i <= n; j++) {
st[prime[j] * i] = 1;
if (i % prime[j] != 0) mu[i * prime[j]] = -mu[i];
else { mu[prime[j] * i] = 0; break; }
}
}
for (long long i = 1; i <= n; i++) sum[i] = (sum[i - 1] + mu[i] * 1ll * i * i % mod + mod) % mod;
}
long long n, m;
long long Sum(long long x, long long y) {
return (x * (x + 1) / 2 % mod) * (y * (y + 1) / 2 % mod) % mod;
}
inline long long query(long long x, long long y) {
long long ans = 0;
for (long long l = 1, r; l <= min(x, y); l = r + 1) {
r = min(x / (x / l), y / (y / l));
ans = ans + ((sum[r] - sum[l - 1] + mod) * 1ll * Sum(x / l, y / l) % mod) % mod;
}
return ans;
}
int main() {
scanf("%lld%lld", &n, &m);
init(1e7);
long long ans = 0;
for (long long l = 1, r; l <= min(n, m); l = r + 1) {
r = min(n / (n / l), m / (m / l));
ans = (ans + ((r - l + 1) * (l + r) / 2 % mod * (query(n / l, m / l)) % mod)) % mod;
}
printf("%lld\n", ans);
return 0;
}
T8 P3327 【SDOI2015】约数个数和
题目描述
设 $d(x)$ 为 $x$ 的约数个数,给定 $n,m$,求
$$\sum_{i=1}^n\sum_{j=1}^md(ij)$$
已知一个公式:$d(ij) = \sum_{x|i} \sum_{y|j} [\gcd(x,y) == 1]$
则:$Ans = \sum_{i=1}^{n} \sum_{j=1}^{m} \sum_{x|i} \sum_{y|j} [\gcd(x,y) == 1]$
转化式子:$\sum_{i=1}^{n} \sum_{j=1}^{m} \lfloor \frac{n}{i} \rfloor \lfloor \frac{m}{j} \rfloor [\gcd(x,y) == 1]$
开始莫反:$f(x)=\sum_{i=1}^{n} \sum_{j=1}^{m} \lfloor \frac{n}{i} \rfloor \lfloor \frac{m}{j} \rfloor [\gcd(x,y) == x]$
$g(x) = \sum_{x|d} f(d)$
$g(x) = \sum_{i=1}^{\frac{n}{x}} \sum_{j=1}^{\frac{m}{x}} \lfloor \frac{n}{ix} \rfloor \lfloor \frac{m}{jx} \rfloor$
同时表示出 $f$ 函数:
$f(n) = \sum_{n|d} \mu(\frac{d}{n}) g(d)$
答案明显是 $f(1)$:
$Ans = f(1) = \sum_{i=1}^{n} \mu(i) g(i)$
最后是计算 $g(i)$ 的问题:先计算 $s(n) = \sum_{i=1}^{n} \lfloor \frac{n}{i} \rfloor$
这样 $Ans$ 即可分为前后两部分($\mu(i)$ 和 $g(i)$)计算。
前面 $\mu$ 直接线性筛并前缀和,后面 $g$ 函数用 $s$ 直接求解。
#include <bits/stdc++.h>
using namespace std;
const long long N = 5e4 + 10;
long long s[N], mu[N], tot = 0, prime[N], sum[N];
bool st[N];
inline void init(long long n) {
sum[1] = mu[1] = 1;
for (register long long i = 2; i <= n; i++) {
if (!st[i]) prime[++tot] = i, mu[i] = -1;
for (register long long j = 1; j <= tot && prime[j] * i <= n; j++) {
st[prime[j] * i] = 1;
if (i % prime[j] != 0) mu[i * prime[j]] = -mu[i];
else { mu[prime[j] * i] = 0; break; }
}
sum[i] = sum[i - 1] + mu[i];
}
for (long long i = 1; i <= n; i++) {
for (long long l = 1, r; l <= i; l = r + 1) {
r = i / (i / l);
s[i] += (r - l + 1) * (i / l);
}
}
}
long long n, m;
int main() {
long long T; scanf("%lld", &T);
init(5e4);
while (T--) {
scanf("%lld%lld", &n, &m);
if (n > m) swap(n, m);
long long ans = 0;
for (long long l = 1, r; l <= n; l = r + 1) {
r = min(n / (n / l), m / (m / l));
ans += (sum[r] - sum[l - 1]) * s[n / l] * s[m / l];
}
printf("%lld\n", ans);
}
return 0;
}
T9 P4449 于神之怒加强版
题目描述
给定 $n,m,k$,计算
$$\sum_{i=1}^n \sum_{j=1}^m \gcd(i,j)^k$$
对 $10^9 + 7$ 取模的结果。
$\sum_{i=1}^n \sum_{j=1}^m \gcd(i,j)^k$
枚举 $\gcd$,得:
$\sum_{i=1}^{n} \sum_{j=1}^{m} \sum_{d=1}^{n} d^{k} [\gcd(i,j) == 1]$
$\sum_{d=1} d^{k} \sum_{i=1}^{\lfloor \frac{n}{d} \rfloor} \sum_{j=1}^{\lfloor \frac{m}{d} \rfloor} \sum_{x|i,x|j} \mu(x)$
$\sum_{d=1}^{n} d^{k} \sum_{x=1} \mu(x) \lfloor \frac{n}{dx} \rfloor \lfloor \frac{m}{dx} \rfloor$
$\sum_{d=1}^{n} d^k \sum_{x=1} \mu(x) \lfloor \frac{n}{dx} \rfloor \lfloor \frac{m}{dx} \rfloor$
简化式子,设 $T = dx$:
$\sum_{T=1}^{n} \lfloor \frac{n}{T} \rfloor \lfloor \frac{m}{T} \rfloor \sum_{d|T} d^{k} \mu(\frac{T}{d})$
插入证明积性函数的卷积仍是积性函数
设 $f(x)$、$g(x)$ 都是积性函数。
设 $a$ 和 $b$,其中 $\gcd(a,b) == 1$。
设 $h(a) = \sum_{x|a} f(a) g(\frac{a}{x})$
$h(b) = \sum_{y|b} f(b) g(\frac{b}{y})$
接下来证明 $h(a)h(b) == h(ab)$
$h(a)h(b) = \sum_{x|a} f(a) g(\frac{a}{x}) \sum_{y|b} f(b) g(\frac{b}{y})$
$= \sum_{d|ab} f(d) g(\frac{ab}{d})$
$= h(ab)$
回到原式:$\sum_{T=1}^{n} \lfloor \frac{n}{T} \rfloor \lfloor \frac{m}{T} \rfloor \sum_{d|T} d^{k} \mu(\frac{T}{d})$
只观察后半部分:$\sum_{d|T} d^{k} \mu(\frac{T}{d})$
很明显 $d^k$ 和 $\mu$ 都是积性函数,而且这是一个卷积的形式。
因此利用上面插入证明的结论:积性函数的卷积仍是积性函数。
也就是说 $g(T) = \sum_{d|T} d^{k} \mu(\frac{T}{d})$ 也是积性函数。
众所周知积性函数可以用线性筛。因此 $g$ 函数也可以用筛法。
下面分类讨论两种情况:
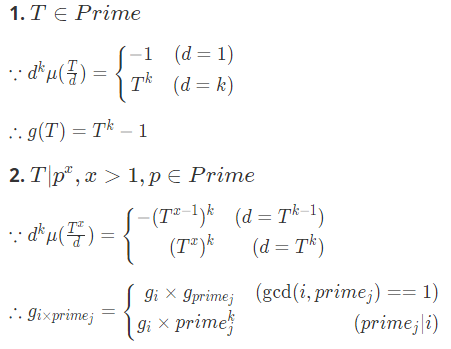
线性筛 $g$ 函数即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 5e6 + 10;
const int mod = 1e9 + 7;
bool st[N];
int prime[N], tot = 0, g[N], ksm[N];
int qmi(int a, int b) {
int res = 1 % mod;
while (b) {
if (b & 1) res = (long long)res * a % mod;
a = (long long)a * a % mod;
b >>= 1;
}
return res;
}
int k;
void init(int n) {
g[1] = 1;
for (int i = 2; i <= n; i++) {
if (!st[i]) prime[++tot] = i, ksm[tot] = qmi(i, k), g[i] = (ksm[tot] - 1) % mod;
for (int j = 1; j <= tot && i * prime[j] <= n; j++) {
int p = prime[j] * i;
st[p] = 1;
if (i % prime[j] == 0) {
g[p] = 1ll * ksm[j] * g[i] % mod;
break;
}
g[p] = 1ll * g[i] * g[prime[j]] % mod;
}
}
for (int i = 2; i <= n; i++) g[i] += g[i - 1], g[i] %= mod;
}
int T, n, m;
int main() {
scanf("%d%d", &T, &k);
init(N - 5);
while (T--) {
scanf("%d%d", &n, &m);
int ans = 0;
for (int l = 1, r; l <= min(n, m); l = r + 1) {
r = min(n / (n / l), m / (m / l));
ans += ((g[r] - g[l - 1] + mod) % mod * 1ll * (n / l) % mod * (m / l) % mod) % mod;
ans %= mod;
}
printf("%d\n", ans);
}
return 0;
}
T10 P3312 【SDOI2014】数表
题目描述
有一张 $n\times m$ 的数表,其第 $i$ 行第 $j$ 列($1\le i\le n$,$1\le j\le m$)的数值为能同时整除 $i$ 和 $j$ 的所有自然数之和。给定 $a$,计算数表中不大于 $a$ 的数之和。
简化题意:求 $\sum_{i=1}^{n} \sum_{j=1}^{m} \sigma(\gcd(i,j)) [\sigma(\gcd(i,j)) \leq a]$
其中 $\sigma(x)$ 表示 $x$ 的约数和。
目前考虑没有 $a$ 的限制的情况。
则 $ans = \sum_{d=1}^{\min(n,m)} \sigma(d) \sum_{i=1}^{\lfloor \frac{n}{d} \rfloor} \sum_{j=1}^{\lfloor \frac{m}{d} \rfloor} [\gcd(i,j)==1]$
$\sum_{d=1}^{\min(n,m)} \sigma(d) \sum_{i=1}^{\lfloor \frac{n}{d} \rfloor} \sum_{j=1}^{\lfloor \frac{m}{d} \rfloor} \sum_{k|i,k|j} \mu(k)$
$\sum_{d=1}^{\min(n,m)} \sigma(d) \sum_{k=1}^{\lfloor \frac{\min(n,m)}{d} \rfloor} \mu(k) \lfloor \frac{n}{dk} \rfloor \lfloor \frac{m}{dk} \rfloor$
设 $T=dk$:
$\sum_{T=1}^{\min(n,m)} \sum_{d|T} \sigma(d) \mu(\frac{T}{d}) \lfloor \frac{n}{T} \rfloor \lfloor \frac{m}{T} \rfloor$
加入 $a$ 的限制,考虑用树状数组维护 $\sum_d \sigma(d) \mu(\frac{T}{d})$ 的前缀和。
将线性筛的 $\sigma$ 升序排序,从小到大查询 $a$ 并且更新。
#include <bits/stdc++.h>
using namespace std;
const long long N = 1e5 + 10, M = 2e4 + 10;
const long long mod = (1 << 31);
long long n, prime[N], tot, tree[N], g[N], ans[M], mu[N];
pair<int, int> d[N];
bool st[N];
inline void insert(long long x, long long k) {
for (; x <= N; x += x & -x) tree[x] += k;
}
inline long long query(long long x) {
long long ans = 0;
for (; x; x -= x & -x) ans += tree[x];
return ans;
}
struct ask {
long long n, m, a, id;
long long sol() {
if (n > m) swap(n, m);
long long res = 0;
for (long long l = 1, r; l <= n; l = r + 1) {
r = min(n / (n / l), m / (m / l));
res += ((query(r) - query(l - 1)) * (n / l) * (m / l));
}
return res;
}
} q[M];
bool cmp(ask a, ask b) {
return a.a < b.a;
}
void init() {
mu[1] = 1; d[1] = make_pair(1, 1);
for (long long i = 2; i <= N; i++) {
if (!st[i]) prime[++tot] = i, g[i] = i + 1, mu[i] = -1, d[i] = make_pair(i + 1, i);
for (long long j = 1; j <= tot && i * prime[j] <= N; j++) {
long long x = i * prime[j];
st[x] = 1;
if (i % prime[j] == 0) {
mu[x] = 0;
g[x] = g[i] * prime[j] + 1;
d[x] = make_pair(d[i].first / g[i] * g[x], x);
break;
}
mu[x] = -mu[i];
g[x] = prime[j] + 1;
d[x] = make_pair(d[i].first * d[prime[j]].first, x);
}
}
}
int main() {
init();
long long T; scanf("%lld", &T);
sort(d + 1, d + 1 + N);
for (long long i = 1; i <= T; i++)
scanf("%lld%lld%lld", &q[i].n, &q[i].m, &q[i].a), q[i].id = i;
sort(q + 1, q + 1 + T, cmp);
for (long long i = 1, j = 1; i <= T; i++) {
while (d[j].first <= q[i].a && j <= N) {
for (long long k = d[j].second; k <= N; k += d[j].second) insert(k, d[j].first * mu[k / d[j].second]);
j++;
}
ans[q[i].id] = q[i].sol();
}
for (long long i = 1; i <= T; i++) printf("%lld\n", ans[i] % mod);
return 0;
}
T11 P3704 【SDOI2017】数字表格
题目背景
Doris 刚刚学习了 fibonacci 数列。用 $f_i$ 表示数列的第 $i$ 项,那么
$$f_0=0,f_1=1$$
$$f_n=f_{n-1}+f_{n-2},n\geq 2$$
题目描述
Doris 用老师的超级计算机生成了一个 $n\times m$ 的表格,
第 $i$ 行第 $j$ 列的格子中的数是 $f_{\gcd(i,j)}$,其中 $\gcd(i,j)$ 表示 $i,j$ 的最大公约数。
Doris 的表格中共有 $n\times m$ 个数,她想知道这些数的乘积是多少。
答案对 $10^9+7$ 取模。
简化题意:求 $\prod_{d=1}^{n} \prod_{i=1}^{n} \prod_{j=1}^{m} fib(\gcd(i,j)) [\gcd(i,j) == d]$
其中 $fib(x)$ 是斐波那契数列第 $x$ 项。
化简式子,即提出 $d$:
$\prod_{d=1}^{n} fib(d)^{\sum_{i=1}^{\lfloor \frac{n}{d} \rfloor} \sum_{j=1}^{\lfloor \frac{m}{d} \rfloor} [\gcd(i,j) == 1]}$
$\because \sum_{i=1}^{a} \sum_{j=1}^{b} [\gcd(a,b) == 1]$ 与 $\sum_{d=1}^{a} \lfloor \frac{a}{d} \rfloor \lfloor \frac{b}{d} \rfloor \mu(d)$ 相等,
$\therefore$ 原式 $= \prod_{d=1}^{n} fib(d) ^{\sum_{k} \lfloor \frac{n}{dk} \rfloor \lfloor \frac{m}{dk} \rfloor \mu(k)}$
设 $T=dk$:
$\prod_{T=1}^{n} \prod_{k|T} fib(\frac{T}{k}) ^{\mu(k) \lfloor \frac{n}{T} \rfloor \lfloor \frac{m}{T} \rfloor}$
$=\prod_{T=1}^{n} \prod_{k|T} (fib(\frac{T}{k}) ^{\mu(k)})^{\lfloor \frac{n}{T} \rfloor \lfloor \frac{m}{T} \rfloor}$
对于中间的 $(fib(\frac{T}{k}) ^{\mu(k)})$,可以直接 $n~\log~n$ 预处理前缀和。
对于旁边的指数 $^{\lfloor \frac{n}{T} \rfloor \lfloor \frac{m}{T} \rfloor}$ 可以直接数论分块。
注意当需要以 $\mu$ 为指数的时候,因为 $\mu$ 可能是 $-1$,所以需要预先求出 $fib$ 数组的逆元。
$fib$ 数组直接暴力即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10, mod = 1e9 + 7;
int mu[N], prime[N], tot = 0, sum[N], fib[N], inv_fib[N];
bool st[N];
int read(){
int x = 0; int zf = 1; char ch = ' ';
while (ch != '-' && (ch < '0' || ch > '9')) ch = getchar();
if (ch == '-') zf = -1, ch = getchar();
while (ch >= '0' && ch <= '9') x = x * 10 + ch - '0', ch = getchar(); return x * zf;
}
int qmi(int a, int b, int p) {
int res = 1;
while (b) {
if (b & 1) res = res * 1ll * a % p;
b >>= 1;
a = a * 1ll * a % p;
}
return res;
}
int ny(int a) { return qmi(a, mod - 2, mod); }
inline void init(int n) {
fib[0] = 0, fib[1] = 1;
for (int i = 2; i <= n; i++) fib[i] = (fib[i - 1] + fib[i - 2]) % mod, inv_fib[i] = ny(fib[i]);
mu[1] = 1; inv_fib[1] = 1;
for (register int i = 2; i <= n; i++) {
if (!st[i]) prime[++tot] = i, mu[i] = -1;
for (register int j = 1; j <= tot && prime[j] * i <= n; j++) {
st[prime[j] * i] = 1;
if (i % prime[j] != 0) mu[i * prime[j]] = -mu[i];
else { mu[prime[j] * i] = 0; break; }
}
}
for (int i = 0; i <= n; i++) sum[i] = 1;
for (int i = 1; i <= n; i++) {
if (mu[i] == 0) continue;
for (int j = i; j <= n; j += i) {
sum[j] = (long long) sum[j] * (mu[i] == 1 ? fib[j / i] : inv_fib[j / i]) % mod;
}
}
for (int i = 1; i <= n; i++) sum[i] = (long long) sum[i - 1] * sum[i] % mod;
}
int solve(int n, int m) {
if (n > m) swap(n, m);
int ans = 1;
for (int l = 1, r; l <= n; l = r + 1) {
r = min(n / (n / l), m / (m / l));
ans = (long long) ans * qmi(1ll * sum[r] * ny(sum[l - 1]) % mod, 1ll * (n / l) * (m / l) % (mod - 1), mod) % mod;
}
return ans;
}
int n, m;
int main() {
init(N - 10);
int T; scanf("%d", &T);
while (T--) {
scanf("%d%d", &n, &m);
printf("%d\n", solve(n, m));
}
return 0;
}
Markdown代码超过 1000 行了
T12 CF1780F Three Chairs
题面翻译
给定一个数组$a_1,a_2,\cdots,a_n$,求满足以下条件的三元组$(a_{k_1},a_{k_2},a_{k_3})$个数:
$$
\gcd(\max(a_{k_1},a_{k_2},a_{k_3}), \min(a_{k_1},a_{k_2},a_{k_3}))==1
$$
首先对于 $\gcd(\max(a_{k_1},a_{k_2},a_{k_3}), \min(a_{k_1},a_{k_2},a_{k_3}))==1$,假设 $a_{k_1} \le a_{k_2} \le a_{k_3}$,则原式变为:$\gcd(a_{k_1},a_{k_3}) == 1$。
发现它与 $a_{k_2}$ 没有任何关系。因此只需要枚举最大值和最小值。
那么根据原来的假设,我们先把 $a$ 数组排序,接下来的工作就减轻很多。
答案即对于每个 $d|a_i$,把 $i$ 加入序列 $q$。选择最大最小值以后再挑选中间的数。因此就是挑选 $q_i > q_j$ 的所有数对的 $q_i - q_j - 1$ 之和。
开始莫反:
设 $f(d)$ 表示满足以下条件的三元组 $(a_{k_1},a_{k_2},a_{k_3})$ 的个数 $\gcd(\max(a_{k_1},a_{k_2},a_{k_3}), \min(a_{k_1},a_{k_2},a_{k_3}))==d$
$g(d)$ 表示满足以下条件的三元组 $(a_{k_1},a_{k_2},a_{k_3})$ 的个数 $d| \gcd(\max(a_{k_1},a_{k_2},a_{k_3}), \min(a_{k_1},a_{k_2},a_{k_3}))$
$g(x) = \sum_{x|d} f(d)$
即 $f(x) = \sum_{x|d} \mu(\frac{d}{x}) g(d)$
答案显然为 $f(1)$,即 $\sum_{i=1}^{n} \mu(i) g(i)$
接下来直接按照上述方式解即可。
#include <bits/stdc++.h>
using namespace std;
const long long N = 3e5 + 10;
long long mu[N], prime[N] , tot = 0;
bool st[N];
long long n, a[N];
inline void init(long long n) {
mu[1] = 1;
for (register long long i = 2; i <= n; i++) {
if (!st[i]) prime[++tot] = i, mu[i] = -1;
for (register long long j = 1; j <= tot && prime[j] * i <= n; j++) {
st[prime[j] * i] = 1;
if (i % prime[j] != 0) mu[i * prime[j]] = -mu[i];
else { mu[prime[j] * i] = 0; break; }
}
}
}
long long sum[N], cnt[N];
long long ans;
void work(long long x, long long y) {
if (mu[x] == 0) return;
ans += 1ll * mu[x] * (1ll * (y - 1) * 1ll * cnt[x] - sum[x]);
sum[x] += y; cnt[x]++;
}
int main() {
init(N - 10);
scanf("%d", &n);
for (long long i = 1; i <= n; i++) scanf("%d", &a[i]);
sort(a + 1, a + 1 + n);
for (long long i = 1; i <= n; i++) {
for (long long j = 1; j * j <= a[i]; j++) {
if (a[i] % j != 0) continue;
work(j, i);
if (j * j != a[i]) work(a[i] / j, i);
}
}
printf("%lld\n", ans);
return 0;
}
T13 CF235E Number Challenge
题面翻译
题意:记d(i)表示i的约数个数,输入a,b,c;
求 $\sum_{i=1}^{a} \sum_{j=1}^{b} \sum_{k=1}^{c} d(ijk) \mod(1073741824(2^{30}))$ 的值。
其中 $d(i)$ 表示 $i$ 的约数个数。
回顾 T8 P3327 【SDOI2015】约数个数和
其中给出了一个公式。这里拓展到三个数的情况:
将原公式修改为:$\sum_{i=1}^{A} \sum_{j=1}^{B} \sum_{k=1}^{C} \sum_{a|i} \sum_{b|j} \sum_{c|k} [\gcd(a,b,c) == 1]$
$\sum_{a=1}^{A} \sum_{b=1}^{B} \sum_{c=1}^{C} \sum_{a|i} \sum_{b|j} \sum_{c|k} [\gcd(a,b,c) == 1]$
$\sum_{a=1}^{A} \sum_{b=1}^{B} \sum_{c=1}^{C} \lfloor \frac{A}{a} \rfloor \lfloor \frac{B}{b} \rfloor \lfloor \frac{C}{c} \rfloor [\gcd(a,b,c) == 1]$
$\sum_{i=1}^{A} \sum_{j=1}^{B} \sum_{k=1}^{C} \lfloor \frac{A}{i} \rfloor \lfloor \frac{B}{j} \rfloor \lfloor \frac{C}{k} \rfloor [\gcd(i,j,k) == 1]$
$\sum_{i=1}^{A} \sum_{j=1}^{B} \sum_{k=1}^{C} \lfloor \frac{A}{i} \rfloor \lfloor \frac{B}{j} \rfloor \lfloor \frac{C}{k} \rfloor \sum_{d|\gcd(i,j)} \mu(d) [\gcd(i,k) == 1][\gcd(j,k) == 1]$
$\sum_{k=1}^{C} \sum_{d=1}^{\min(A,B)} \mu(d) \sum_{i=1}^{\lfloor \frac{A}{d} \rfloor} \lfloor \frac{A}{id} \rfloor [\gcd(id,k) == 1] \sum_{j=1}^{\lfloor \frac{B}{d} \rfloor} \lfloor \frac{B}{id} \rfloor [\gcd(jd,k) == 1]$
这个公式就是此题答案了。
在上代码之前有两个优化:
- 预处理 $\sum_{i=1}^{\lfloor \frac{A}{d} \rfloor} \lfloor \frac{A}{id} \rfloor [\gcd(id,k) == 1]$ 和 $\sum_{j=1}^{\lfloor \frac{B}{d} \rfloor} \lfloor \frac{B}{id} \rfloor [\gcd(jd,k) == 1]$
- 用数组记录两个数是否互质。(即后面的判定条件 $[\gcd(…~,~…) == 1]$
代码:
#include <bits/stdc++.h>
using namespace std;
const long long N = 2e3 + 10;
const long long mod = 1073741824;
long long n, m;
long long tot, prime[N], mu[N], sum[N];
long long a, b, c;
bool st[N];
long long gcd(int a, int b) // 欧几里得算法
{
return b ? gcd(b, a % b) : a;
}
inline void init1(long long n) {
sum[1] = mu[1] = 1;
for (long long i = 2; i <= n; i++) {
if (!st[i]) prime[++tot] = i, mu[i] = -1;
for (long long j = 1; j <= tot && prime[j] * i <= n; j++) {
st[prime[j] * i] = 1;
if (i % prime[j] != 0) mu[i * prime[j]] = -mu[i];
else { mu[prime[j] * i] = 0; break; }
}
sum[i] = sum[i - 1] + mu[i];
}
}
long long A[N][N], B[N][N], have[N][N];
void init2() {
for (long long i = 1; i <= 2000; i++)
for (long long j = 1; j <= 2000; j++)
if (gcd(i, j) == 1) have[i][j] = true; //互质
for (long long k = 1; k <= c; k++)
for (long long d = 1; d <= min(a, b); d++) {
for (long long i = 1; i <= a / d; i++)
if (have[k][i * d]) //互质
A[k][d] = (A[k][d] + a / (i * d)) % mod;
for (long long i = 1; i <= b / d; i++)
if (have[k][i * d]) //互质
B[k][d] = (B[k][d] + b / (i * d)) % mod;
}
}
int main() {
scanf("%d%d%d", &a, &b, &c);
init1(2000), init2(); //预处理
long long ans = 0;
for (long long k = 1; k <= c; k++) { //公式中最外层循环
long long res = 0;
for (long long d = 1; d <= min(a, b); d++)
res = (res + mu[d] % mod * A[k][d] * B[k][d] % mod) % mod;
ans = (ans + res * (c / k) % mod) % mod;
}
printf("%lld\n", (ans % mod + mod) % mod);
return 0;
}
到这里这 $13$ 题就结束了
公式有点多,我就写了大概两三周的样子。。。
第十三题是我生病的时候写的


数学大佬!
个人感觉可以出个配套洛谷题单放个链接
啊啊啊题目列表被我们机房组织的同学删了
结果我现在根本不知道还有哪些题我没写题解。。。
放了
orz
qp
后排支持
后排次瓜拜谢,现在都只会六道AWA。
现在让我做估计一题都咕不出来了
还有您可以看看这个(https://www.acwing.com/blog/content/58104/)
https://www.acwing.com/blog/content/58104/
(方便直接点)
orz
sto
高中生大佬吗?
初一
呜呜呜呜你是我哥tql,大学生自愧不如
你也都是跟y‘总学的吗
训练队自己整的
$\color{red}{o}$$\color{blue}{r}$$\color{orange}{z}$
orz
orz
这下火了
%%%%%%%%%%%%%%%%%