前言
宣传: 算法主页
前置知识
多项式
一个多项式表示为 $A(x) = a_0 + a_1 x + a_2 x^2 + … a_n x^n$
系数表示法: $A(x) = \sum _{i=0}^{n} a_i x^i$
点值表示法:用 $n$ 个不同的点 $(x, A(x))$ 唯一表示多项式 $A(x)$
复数
前置知识:向量、三角函数
定义
设 $i^2 = -1$ ,则一个复数表示为 $a + bi (a,b\in R)$
其中 $bi$ 为虚部, $a$ 为实部
复平面上,从 $(0,0)$ 到 $(a,b)$ 的向量表示 $a+bi$
棱长: $|Z| = \sqrt{a^2+b^2}$
幅角:为从 $x$ 正半轴逆时针旋转的角度
运算
加法: $(a+bi)+(c+di) = (a+c)+(b+d)i$
乘法: 几何意义:复数相乘,模长相乘,幅角相加
$\ \ \ \ \ \ \ \ \ \ \ $代数意义:$(a+bi)(c+di) = (ac-bd)+(ad+bc)i$
共轭复数
复数 $Z = a+bi$ 的共轭复数 $\bar{Z}$ 为 $a-bi$
$|Z|=|\bar{Z}|\ \ \ \ \ \ \ \ Z\cdot \bar{Z} = a^2+b^2$
复数除法
$z_1=a_1+b_1i,z_2=a_2+b_2i$
设 $z_0=\frac{z_1}{z_2}$
上下同乘 $z_2$ 的共轭复数 $\bar{z_2}$
$$\frac{z_1 \bar{z_2}}{a_2^2 + b_2^2}$$
单位根 $\omega $
为在复平面上以原点为圆心作半径为 $1$ 的圆。
$\omega_n^k $ 表示为将圆分成 $n$ 份,从 $x$ 正半轴逆时针取 $k$ 份下的复数。
-
$\omega_n^k = \omega _{n}^{k-1} \cdot \omega _n^1$
-
$\omega_n^0 = \omega_n^n=1$
-
$\omega_{2n}^{2k} = \omega_n^k$
-
$\omega_n^{k+\frac{n}{2}} = - \omega_n^k$
算法流程
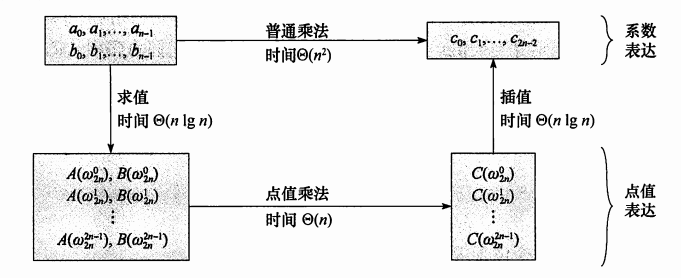
快速傅里叶变换
快速傅里叶变换($\texttt{Fast Fourier Transform , FFT}$)
使用 $\omega_n^k (0\leq k < n)$ 这 $n$ 个不同的数来当作点值表示法中的 $n$ 个 $x$
已知
$$A(x) = \sum_{i=0}^{n-1} a_i * x^i$$
设
$$A_1(x) = a_0 + a_2 \cdot x + a_4 \cdot x^2 + \cdots + a_{n-2} x^{\frac{n}{2}-1}$$
$$A_2(x) = a_1 + a_3 \cdot x + a_5 \cdot x^2 + \cdots + a_{n-1} x^{\frac{n}{2}-1}$$
则
$$A(x) = A_1(x^2) + xA_2(x^2)$$
将 $\omega_n^k (0\leq k < n)$ 代入 $A(x)$ 中
$$A(\omega_n^k) = A_1(\omega_{\frac{n}{2}}^{k}) + \omega_n^k A_2(\omega_{\frac{n}{2}}^{k})$$
$$A(\omega_n^{\frac{n}{2}+k}) = A_1(\omega_{\frac{n}{2}}^{k}) - \omega_n^k A_2(\omega_{\frac{n}{2}}^{k})$$
两个式子 $A_1()$ ,$A_2()$ 相同。
当计算 $[0,\frac{n}{2})$ 时,$[\frac{n}{2},n)$ 可以直接计算。
每次计算量减小一半,时间复杂度 $O(n\log n)$
快速傅里叶逆变换
快速傅里叶逆变换 $(\texttt{Inverse Fast Fourier Transform , IFFT})$
设 $C(x) = c_0 + c_1 x + c_2 x^2 + \cdots + c_{n - 1} x^{n-1}$
设 $b_i = \omega_n^i, y_i = C(b_i)$
$C(x)$ 经过 $n$ 个点,$(b_0, y_0) \dots (b_{n - 1}, y_{n - 1}) $
引理1
设
$$S(x) = 1 + x + x^2 + \cdots + x^{n-1}$$
因为
$$S(\omega_n^k) = \omega_n^0 + \omega_n^k + \omega_n^{2k} + \cdots + \omega_n^{(n-1)k}$$
又
$$\omega_n^k S(\omega_n^k) = \omega_n^k + \omega_n^{2k} + \cdots + \omega_n^{(n-1)k} + \omega_n^{nk}$$
所以
若 $k\not= 0$
则
$$S(\omega_n^k) = \frac{0}{1 - \omega_n^k} = 0$$
若 $k=0$
则
$$S(\omega_n^k) = n$$
引理2
$$nc_k = \sum_{i=0}^{n-1} y_i (w_n^{-k})^i$$
证明
$$\sum_{i=0}^{n-1} y_i (w_n^{-k})^i$$
$$=\sum_{i=0}^{n-1} (\sum_{j=0}^{n-1} c_j {(w_n^i)}^{j}) (w_n^{-k})^i$$
$$=\sum_{i=0}^{n-1} (\sum_{j=0}^{n-1} c_j {(w_n^j)}^{i}) (w_n^{-k})^i$$
$$=\sum_{i=0}^{n-1} (\sum_{j=0}^{n-1} c_j {(w_n^{j - k})}^{i})$$
$$=\sum_{j=0}^{n-1} c_j \sum_{i=0}^{n-1} (w_n^{j-k})^{i}$$
$$=\sum_{j=0}^{n-1} c_j S(w_n^{j-k})$$
$$=nc_k$$
证毕
设
$$D(x) = \sum_{i=0}^{n-1} y_i x^i$$
则
$$c_k = \frac{D(w_n^{-k})}{n}$$
所以再做一次快速傅里叶变换即可
$实现$
#include <bits/stdc++.h>
using namespace std;
const int N = 400010;
const double PI = acos(-1);
int n, m, tot;
int rev[N];
struct Complex
{
double x, y;
Complex operator+ (const Complex& t) const
{
return {x + t.x, y + t.y};
}
Complex operator- (const Complex& t) const
{
return {x - t.x, y - t.y};
}
Complex operator* (const Complex& t) const
{
return {x * t.x - y * t.y, x * t.y + y * t.x};
}
} a[N], b[N];
void fft(Complex a[], int inv)
{
for (int i = 0; i < tot; i ++ )
if (i < rev[i])
swap(a[i], a[rev[i]]);
for (int mid = 1; mid < tot; mid <<= 1)
{
Complex w1 = {cos(PI / mid), inv * sin(PI / mid)};
for (int i = 0; i < tot; i += mid * 2)
{
Complex wk = {1, 0};
for (int j = 0; j < mid; j ++ , wk = wk * w1)
{
Complex x = a[i + j], y = wk * a[i + j + mid];
a[i + j] = x + y, a[i + j + mid] = x - y;
}
}
}
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i <= n; i ++ ) scanf("%lf", &a[i].x);
for (int i = 0; i <= m; i ++ ) scanf("%lf", &b[i].x);
int bit = 0;
while ((1 << bit) <= n + m) bit ++ ;
tot = 1 << bit;
for (int i = 0; i < tot; i ++ )
rev[i] = (rev[i >> 1] >> 1) + ((i & 1) << (bit - 1));
fft(a, 1), fft(b, 1);
for (int i = 0; i < tot; i ++ ) a[i] = a[i] * b[i];
fft(a, -1);
for (int i = 0; i <= n + m; i ++ )
printf("%d ", (int)(a[i].x / tot + 0.5));
return 0;
}

