1 DFS 排列数字
#include<bits/stdc++.h>
using namespace std;
const int N = 10;
int path[N]; //保存路径
bool st[N]; // 判断数字是否使用过
int n;
void dfs(int u)
{
if (u > n) // 因为 1 2 3都用了传过来4 结束
{
for (int i = 1; i <= n; i ++) // 输出方案
cout << path[i] << " " ;
cout << endl;
}
for (int i = 1; i <= n; i ++)
{
if (!st[i]) //空位上可以选择的数字为:1 ~ n
{
path[u] = i; //如果数字 i 没有被用过
st[i] = true; // 数字被用了修改状态
dfs(u + 1); //下一位
st[i] = false; //回溯
}
}
}
int main ()
{
cin >> n;
dfs(1);
}
2.n皇后
#include<iostream>
using namespace std;
const int N=20;//对角线是2N-1 ?
int path[N];
char g[N][N];
bool col[N],dg[N],udg[N];//col 列 dg主对角线 udg右对角线 u+i
int n;
void dfs(int u)
{
if(u==n) //表示已经搜了n行,故输出这条路径 因为是从0ka
{
for(int i=0;i<n;i++) cout<<g[i]<<endl;
puts("");//换行
return ;
}
//对n个位置按行搜索
for(int i=0;i<n;i++)
// 剪枝(对于不满足要求的点,不再继续往下搜索)
// udg[n - u + i],+n是为了保证下标非负
if (!col[i] && !dg[u + i] && !udg[n - u + i]) // 截距
{
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n - u + i] = true;
dfs(u + 1);
col[i] = dg[u + i] = udg[n - u + i] = false; // 恢复现场 这步很关键
g[u][i] = '.';
}
}
int main()
{
cin>>n;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++)
{
g[i][j] = '.';
}
}
dfs(0);
return 0;
}
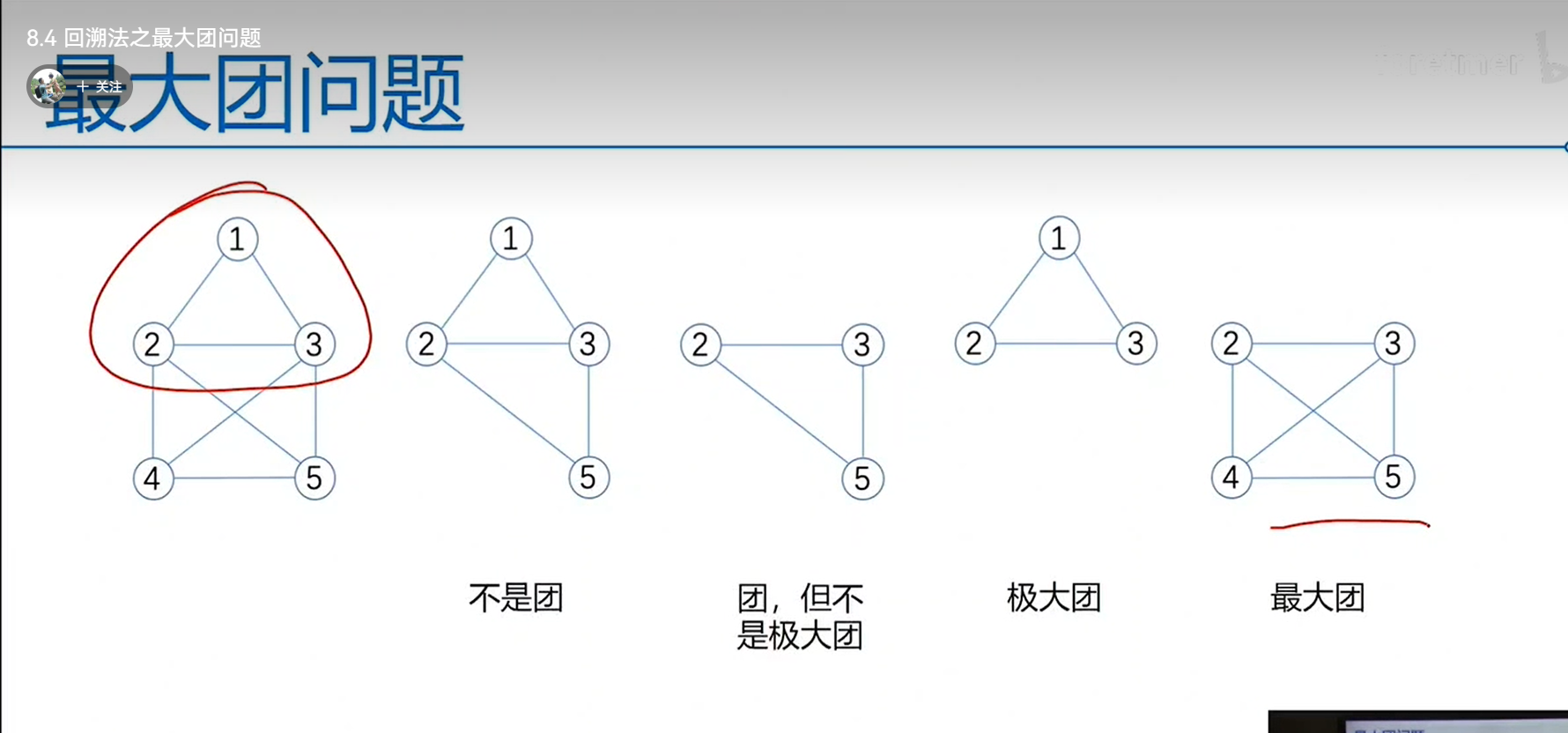
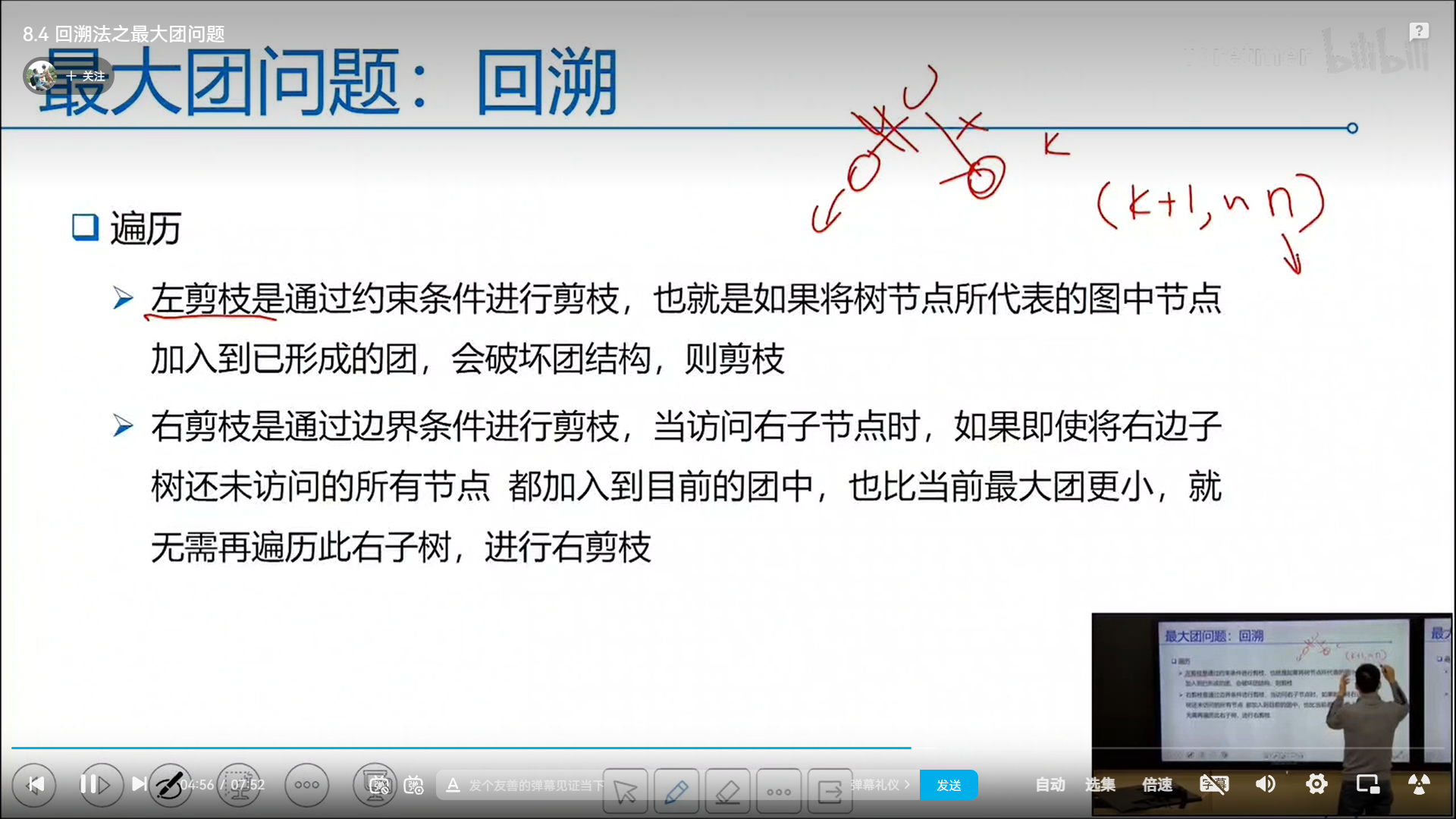
3最大团 回溯

4.BFS 走迷宫
#include<bits/stdc++.h>
using namespace std;
const int N = 110;
int f[N][N];
int g[N][N];
int n, m;
typedef pair<int, int> PII;
int bfs(int a, int b)
{
queue<PII> q;
q.push({a,b}); // pii;
while (!q.empty())
{
PII start = q.front();
q.pop();
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
for (int i = 0; i < 4; i ++)
{
int x = start.first + dx[i];
int y = start.second + dy[i];
if (g[x][y] == 0)
{
g[x][y] = 1;
f[x][y] = f[start.first][start.second] + 1;
q.push({x,y});
}
}
}
cout << f[n][m] ;
}
int main ()
{
memset(g, 1, sizeof(g));//边上是墙
cin >> n >> m;
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= m; j ++)
cin >> g[i][j];
bfs(1, 1);
}
//用队列
5.八数码
#include<iostream>
#include<algorithm>//算法
#include<unordered_map>//hash map
#include<queue>//队列
using namespace std;
int bfs(string start)
{
string end="12345678x"; //转换完成后的结果!
queue<string> q;
unordered_map<string,int> d ;//距离数组
//初始化队列和dist数组
q.push(start);
d[start]=0;//起点的距离位0
int dx[4]={-1,0,1,0},dy[4]={0,-1,0,1}; //上下左右
while(q.size())
{
auto t = q.front();// q是一个队列 String类型 STL
q.pop();
int distence =d[t];
//记录当前状态的距离,如果是最终状态则返回距离
if(t==end) return distence;
//状态转移
int k=t.find('x');//find x 返回X 的下标;
int x=k/3,y=k%3; /*小技巧 转化为 三成三矩阵的位置 例如 1234x5678 1 2 3 x的下标为4 位置为(1,1)
4 x 5*/
for(int i=0;i<4;i++){
//a,b为上下左右移动坐标
int a=x+dx[i],b=y+dy[i];
if(a >= 0 && a < 3 && b >= 0 && b < 3) //当前坐标没有越界
{
swap(t[k],t[a*3+b]);//转移x
if(!d.count(t)){ //如果当前状态是第一次遍历,记录距离,入队
d[t]=distence+1;
q.push(t);
}
swap(t[k], t[a * 3 + b]); //还原状态,为下一种转换情况做准备
}
}
}
return -1;
}
int main()
{
string start; //存储初始状态;
for(int i=0;i<9;i++)
{
char c;
cin>>c;
start+=c;
}
cout<<bfs(start)<<endl;
return 0;
}
6.全球变暖
#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
const int N = 1010;
int n;
char g[N][N];
bool st[N][N];
PII q[N * N];
int dx[4] = { -1,0,1,0 };
int dy[4] = { 0,1,0,-1 };
void bfs(int sx, int sy, int &total, int &bound) {
int hh = 0, tt = 0;
q[0] = { sx,sy }; //q.push({sx, sy);
st[sx][sy] = true;
while (hh <= tt) {//while(!q.empty();
PII t = q[hh++];// auto t = q. front(); q.pop();
total++;
bool is_bound = false; //是否临海
for (int i = 0; i < 4; i++) //遍历四个方向
{
int x = t.x + dx[i], y = t.y + dy[i];
if (x < 0 || x >= n || y < 0 || y >= n)continue; //如果出界 跳过
if (st[x][y])continue; //如果访问过
if (g[x][y] == '.') //t的上下左右存在海洋
{
is_bound = true;
continue; //跳出一层循环
}
q[++tt] = { x,y }; //q.push({x, y}); 只有不临海才会加入队列中
st[x][y] = true; //访问
}
if (is_bound)
bound++;
}
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i++)
scanf("%s", g[i]);
int cnt = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (!st[i][j] && g[i][j] == '#') {//没有访问过 并且 为陆地
int total = 0, bound = 0;
bfs(i, j, total, bound);
if (total == bound) cnt++; //群岛有多少个块 有多少个块在边界
//岛屿为一个连通块统计的是多少个群岛会完全淹没
}
}
}
printf("%d\n", cnt);
return 0;
}

