栈[数组模拟]

基本思想

先进后出，很基础的数据结构，不再赘述

存储结构：

int stk[N], tt;//stk[]存的是栈中的所有的元素
//tt是栈顶的指针，指向栈顶元素，严格来说，这时一个满递增的栈

插入操作：

stk[++ tt] = x;

弹出操作:

tt--;

查询栈是否为空（栈底元素从1开始）：

if(tt > 0) not empty;
else empty

栈顶元素：

stk[tt];

代码实现

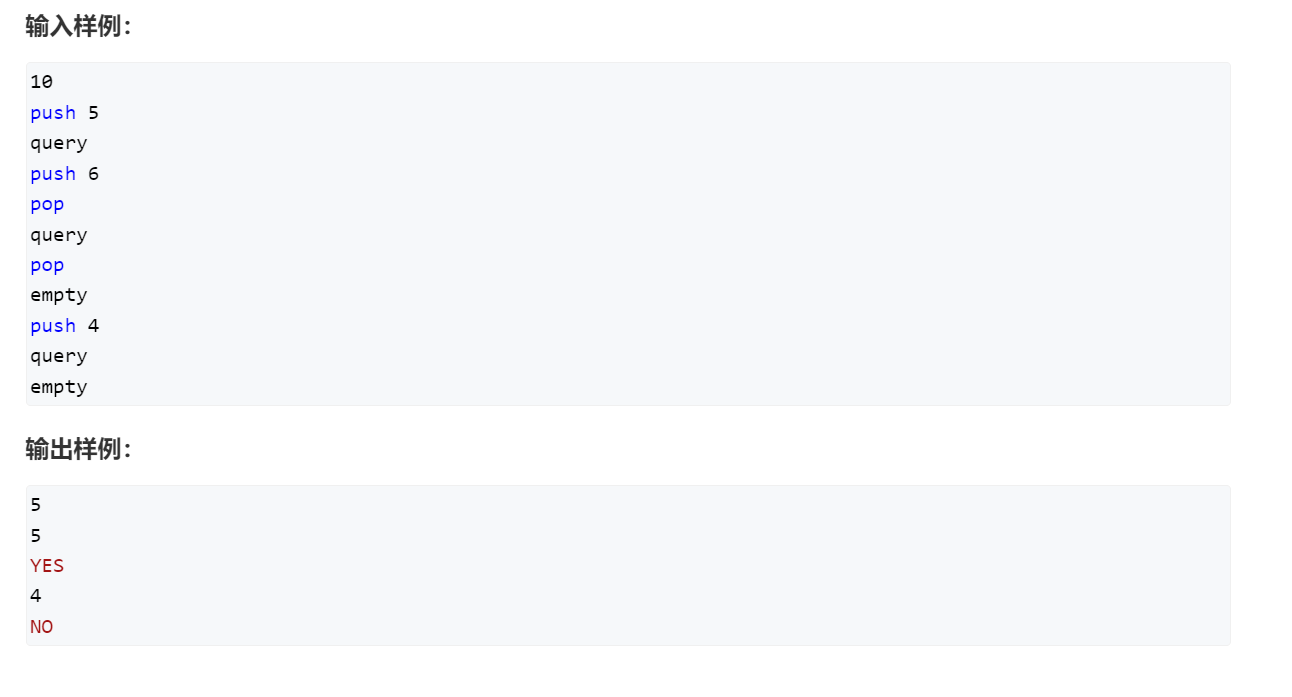
#include<iostream>
using namespace std;

const int N = 100010;

int stk[N], tt;

int main(){
    int m;
    cin >> m;
    while(m --){
        char op[4];
        scanf("%s", op);
        int x;

        if(op[0] == 'p' && op[1] == 'u'){
            scanf("%d", &x);
            stk[++tt] = x;
        }else if(op[0] == 'p' && op[1] == 'o'){
            tt --;
        }else if(op[0] == 'e'){
            if(tt > 0){
                printf("NO\n");
            }else{
                printf("YES\n");
            }
        }else{
            x = stk[tt];
            printf("%d\n", x);
        }
    }

    return 0;
}

单调栈

基本思想

单调栈顾名思义，栈中的数据是单调的，这种数据结构一般指用于以下这个题目，我们用一个栈存储数组的元素，假如读到了下标为i的这个数组，如果栈中存在比它大的数，那么在当前情况以及后面所有的情况，这些数都不会作为答案输出，所以我们将栈中的这些数弹出

当i从1开始的时候，我们通过以上操作，就可以保证栈中的元素始终是递增的，并且每次的答案都是栈顶元素

代码实现

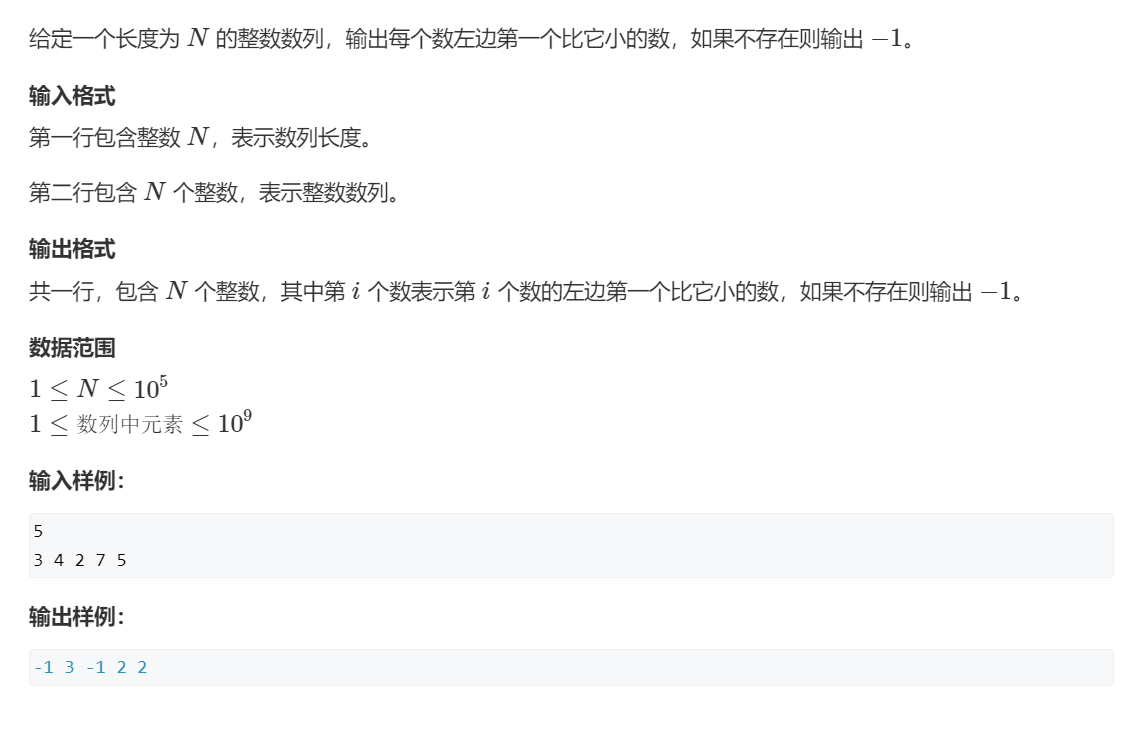
#include<iostream>
using namespace std;
const int N = 100010;

int stk[N], tt;

int main(){
    int n;
    cin >> n;
    for(int i = 1; i <= n; i ++){
        int x;
        scanf("%d", &x);
        while(tt && stk[tt] >= x) tt --;
        if(tt == 0) cout << -1 << " ";
        else cout << stk[tt] <<" ";
        tt ++ ;
        stk[tt] = x;
    }
    return 0;
}

队列

基本思想

队列的话就是先进先出的数据结构，不再赘述

存储结构：

int q[N];//用来存储队列中的元素
int hh;//队头指针
int tt = -1;//队尾指针，一开始指向-1，表示队列中没有元素

插入元素：

q[++ tt] = x;//在队尾插入一个元素，队列中的元素下标从0开始，与栈有点点不同

弹出元素：

hh++;//队头指针往后移动一个即表示弹出一个元素

判断队是否为空：

if(hh <= tt) not empty;//队中有一个元素的情况下tt是等于hh的
else empty;

取出队列头元素：

x = q[hh];

代码实现

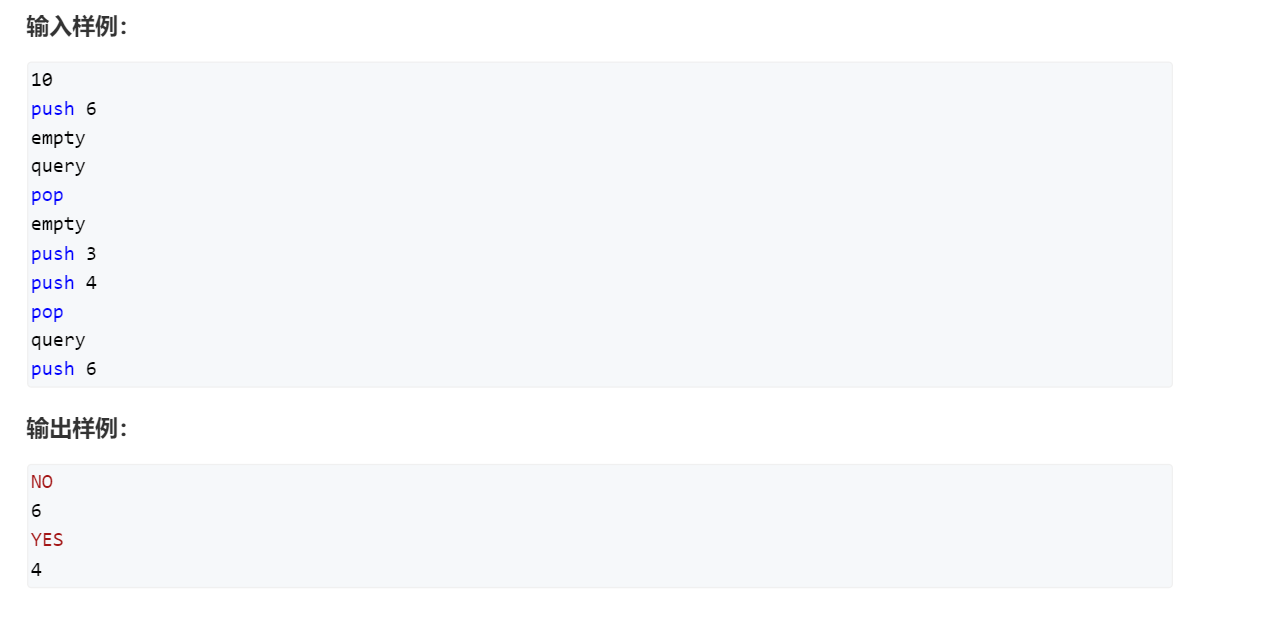
#include<iostream>
using namespace std;

const int N = 100010;

int q[N], hh, tt = -1;

int main(){
    int m;
    cin >> m;

    while(m --){
        char op[4];
        scanf("%s", op);
        int x;

        if(op[0] == 'p' && op[1] == 'u'){
            scanf("%d", &x);
            q[++tt] = x;
        }else if(op[0] == 'p' && op[1] == 'o'){
            hh++;
        }else if(op[0] == 'e'){
            if(hh <= tt){
                printf("NO\n");
            }else{
                printf("YES\n");
            }
        }else if(op[0] == 'q'){
            x = q[hh];
            printf("%d\n", x);
        }
    }

    return 0;
}

单调队列

滑动窗口

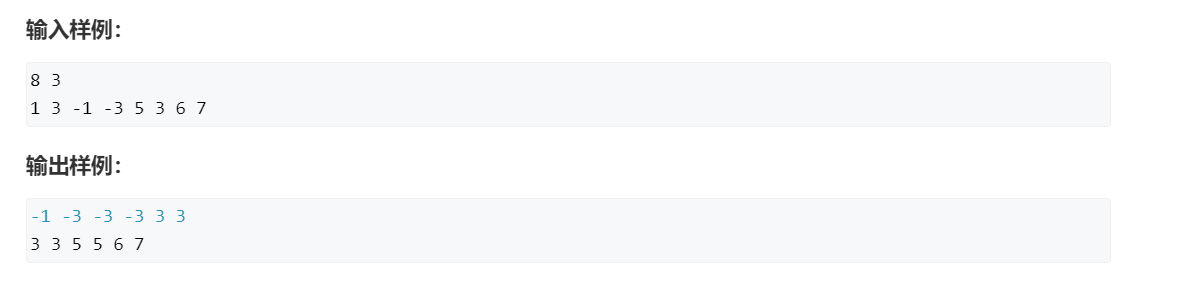
基本思想：

1. 在窗口的移动过程中，新加入一个元素进窗口，若这个元素比窗口中的其他元素都要小，则在后面窗口滑动过程中窗口中的其他元素既比这个元素先移出窗口，又比这个元素小，所以其他元素始终不会作为窗口的最小值输出
2. 我们通过构造一个队列来维护窗口的最小值，队列中的元素是在窗口中的数组元素的下标，并去掉此时窗口中永远不会作为答案的元素。当窗口滑动一次，就把滑进窗口元素的下标加入到队列中，并弹出队列中所有比这个元素大的元素的下标来保证队列的单调性，保证队列的首元素是窗口中的最小元素，通过这个做法我们去掉了窗口的无用元素
3. 但同时，在窗口滑动的过程中我们必须还得考虑队首元素被移出窗口的情况，而且由于窗口只滑动一次，所以每次必然只是队列中的第一个元素可能滑出窗口
4. 由于数组元素就只有两种操作，入窗口（入队列），出队列，所以时间复杂度是O(n)，而暴力算法的时间复杂度是O(nk)，k是窗口的长度

需要注意的几个地方：

1. 队列q[]中元素满足：
   1. 队列中的每个元素都在窗口中
   2. 队首元素是窗口的最小值
   3. 队列中存放的元素是a[]的下标
   4. 严格的讲，队列中的元素可以说是在窗口滑动过程中可能出现的最小元素的下标
2. i - k + 1表示的是窗口的首元素下标，当其大于队首元素时，表示此时的队首元素被移出了窗口，元素不合法，需要将这个元素出队列
3. 窗口包括两个阶段
   1. 窗口形成阶段
   2. 窗口滑动阶段
   3. 窗口滑动是用i++进行模拟的
4. 当窗口滑动一次时，必须先将这时滑进窗口的元素加进队列，再输出队列的首元素，因为这个滑进窗口元素可能会成为队列的首元素，若不在输出答案之前加入队列，可能输出的是原来的队列首元素，答案错误

基本过程：

（以1 3 -1 -3 5 3 6 7为例，窗口的长度是3)

1. i从头开始遍历，首先是第一个元素1，进入窗口，同时把它的下标下入到队列中
   1. 队列:0
   2. 窗口：1
2. i = 1，加入第二个元素进入窗口
   1. 队列：0 1
   2. 窗口：1 3
3. i = 2加入第三个元素进入窗口并且其下标加入队列
   1. 队列：0 1 2
   2. 窗口：1 3 -1
   3. -1小于3和1当窗口滑动的时候3和1会比-1先滑出窗口并且-1总是小于3和1所以3和1永远不会出现在窗口的最小值中，所以可以将这两个数的下标从队列中弹出
   4. 于是将队列里的有些元素弹出得到新的队列：
   5. 队列：2
   6. 窗口：1 3 -1
   7. 由于此时窗口形成，故输出窗口的最小值-1, 接下来开始滑动
4. i = 3，窗口滑动一次，先加入队列，然后再判断
   1. 队列：2 3
   2. 窗口：3 -1 -3
   3. -3小于-1，所以-1出队列
   4. 队列：3
   5. 窗口：3 -1 -3
   6. 输出最小值：-3
5. i = 4，窗口滑动一次
   1. 队列：3 4
   2. 窗口：-1 -3 5
   3. 5大于-3此时不从队列中弹出元素，但是我们需要注意的是，当窗口滑动的过程中，队首元素一直都是窗口里最小的元素，但是会出现该元素滑出窗口的情况，所以需要用此时的窗口首元素下标i - k + 1与队列的首元素进行比较，当i - k + 1 < q[hh]就说明队首元素始终在窗口中
   4. 队列和窗口不变，输出最小值：-3
6. i = 5 ，窗口滑动一次，并加入队列
   1. 队列：3 4 5
   2. 窗口：-3 5 3
   3. 3小于5说明，5在后面的窗口滑动过程中始终不会输出，于是可以将其弹出队列
   4. 队列：3 5
   5. 窗口：-3 5 3
   6. 输出最小元素-3
7. i = 6,窗口滑动一次，并加入队列
   1. 队列：3 5 6
   2. 窗口：5 3 6
   3. 可以看到，此时队首元素已经滑出窗口i - k + 1 > q[hh]所以此时需要将队首元素移出即hh ++，来保证队中的元素都是窗口中的元素
   4. 队列：5 6
   5. 窗口：5 3 6
   6. 6大于队列中下标对应的元素，顾此时不会因为保持队列单调而弹出元素
8. 继续向前滑动，一直到最后一个元素.....

代码实现

#include<iostream>
using namespace std;

const int N = 1000010;

int q[N], tt = -1, hh;
int num[N];

int main(){
    int n, k;
    cin >> n >> k;

    for(int i = 0; i < n; i++){
        cin >> num[i];
    }

    //窗口未形成阶段
    for(int i = 0; i < k; i++){
        while(tt >= hh && num[i] <= num[q[tt]]) tt --;
        q[++tt] = i; 
    }
    cout << num[q[hh]] <<" ";
    //窗口形成后
    for(int i = k; i < n; i ++){
        if(q[hh] < i - (k - 1)) hh ++;//队首元素可能滑出窗口
        while(tt >= hh && num[i] <= num[q[tt]]) tt --;//每滑入一个元素就要与队中的元素进行比较，保证队列的单调性
        q[++tt] = i;
        cout << num[q[hh]] << " ";
    }
    cout <<endl;
    tt = -1; hh = 0;
    //窗口未形成阶段
    for(int i = 0; i < k; i++){
        while(tt >= hh && num[i] >= num[q[tt]]) tt --;
        q[++tt] = i; 
    }
    cout << num[q[hh]] <<" ";
    //窗口形成后
    for(int i = k; i < n; i ++){
        if(q[hh] < i - (k - 1)) hh ++;//队首元素可能滑出窗口
        while(tt >= hh && num[i] >= num[q[tt]]) tt --;//每滑入一个元素就要与队中的元素进行比较，保证队列的单调性
        q[++tt] = i;
        cout << num[q[hh]] << " ";
    }
    return 0;

}