
如何提高能力?
-
上课理解思想
-
默写,最主要是思想
- 看主要思想
- 模板背一遍
- 默写,以题为主,模板题
- 提高熟练度
- 删掉重写,重复三到五次
- 需要注意的是,理解一个算法以后也会忘记的,要反反复复默写背过
排序
快速排序
基本思想
- 找到一个划分的标准元素x,可以是最左边的元素,可以是最右边的元素,也可以是随机的元素,也可以是中间的元素
- 进行划分,将数组变为左边的元素都<=x, 右边的元素都>=x
- 方法一:可以再分配两个数组,扫描后进行合并,共扫描两次(如果忘记方法二的话,直接暴力用这种方法,时间复杂度也是线性的)
- 方法二:交换式,两个下标依次向前移动,然后交换
- 递归处理左右两段
代码实现
void quick_sort(int q[], int l, int r)
{
//递归的终止情况
if(l >= r) return;
//第一步:分成子问题
int i = l - 1, j = r + 1, x = q[l + r >> 1];
while(i < j)
{
do i++; while(q[i] < x);
do j--; while(q[j] > x);
if(i < j) swap(q[i], q[j]);
}
//第二步:递归处理子问题
quick_sort(q, l, j), quick_sort(q, j + 1, r);
//第三步:子问题合并.快排这一步不需要操作,但归并排序的核心在这一步骤
}
边界分析(这里是参考用户醉生梦死的题解)
- 以
j为划分递归时,x不能选择q[r],否则递归会无限划分无法退出,比如数组1,2,若以j划分,则开始时l = 0,r = 1,i = -1, j = 2,循环一次后i = j = 1, l = 0,此时进入递归quick_sort(q, l, j),l仍为0,r仍为1,进入无限递归。同理,当以i进行递归划分时,x不能取q[l] - 在
while循环中,不能加上等号q[i] <= x因为如果这个数组的q[l....r]所有元素都相等的话会导致数组下标越界,看似没有问题,但是如果后面的元素一直<=x则最后下标会一直递增,一直到Memory Limit Exceeded - 第一个
while循环不能用i<=j因为如果数组为1 2然后x = 1则完成while循环后j = -1, i = 1,然后再进入第二个递归又是l = 0, r = 1进入无限递归,但是若i < j则完成while循环后i = j = 0 1,不会进入无限递归 while循环中的if(i < j)可以改成if(i <= j)加上等号也就是再交换一次,没有影响,下一步就直接跳出循环了- 递归中若以
j为划分递归的标准,则不能用quick_sort(q, l, j - 1), quick_sort(q, j, r);因为: - 以数组
2 1 2 1 1为例,划分元素为q[l] = 2,则最后得到的数组为1 1 1 2 2,j =2指向1,i = 3指向2,此时第二个quick_sort(q, j, r)递归的数组为1 2 2不满足快排的思想:右边的数组必须大于等于x - 且
1 2 2进入第二个递归quick_sort(q, j, r)时,始终有l = j (第一个数的下标,不变), r = n-1进入无限递归 - 也可以这样理解,下证
j的取值范围为[l...r-1]- 若
j = r- 说明外循环只进行了一次就退出了,否则
j至少会自减两次,且此时q[j] = q[r] <= x - 由于只进行了一次外循环,所以
q[l...i-1] < x, q[i] >= x,q[j+1...r] > x, q[j] <= x, j <= i - 此时
j = r又由于while循环结束,可得i >= r,i此时不可能为r+1(很显然),所以i = r,于是由于do-while语句可以得到:p[l...i-1] < x且p[i] = p[r] >= x - 所以此时必有
p[r] = x但很显然这个命题并不能一直成立,当我们取x = q[l + r >>1]的时候就不成立 - 所以
j不会超过r
- 说明外循环只进行了一次就退出了,否则
- 若
j < l- 则由于
do - while语句,有p[l...r] > x显然不成立
- 则由于
- 所以
j的取值范围为[l..r-1] - 所以若递归划分为
quick_sort(q, l, j - 1), quick_sort(q, j, r)时,第二个递归j可以取l从而进入无限递归,而采用模板中的方法第一个递归传递的j始终会减小,第二个j + 1始终增大,所以不会进入无限递归
- 若
归并排序
基本思想
- 确定分界点:
mid = (1+r) >> 2 - 先进行递归排序
- 利用双指针算法归并合二为一
代码实现
int q[N], tmp[N];
//给定需要排序的数组以及左右边界
void merge_sort(int q[], int l, int r){
if(l >= r) return;
int mid = l + r >> 1;
merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);
//i, j分别是划分出的两个数组的指针
//k是临时数组的下标
//由于归并的时候只是归并数组q[N]的一部分,所以i,j是从l以及mid+1开始的
int k = 0, i = l, j = mid + 1;
//进行比较以及归并
while(i <= mid && j <= r){
if(q[i] <= q[j]){
tmp[k++] = q[i++];
}else{
tmp[k++] = q[j++];
}
}
while(i <= mid) tmp[k++] = q[i++];
while(j <= r) tmp[k++] = q[j++];
//将归并后的数组写入原来的数组中
for(i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
}
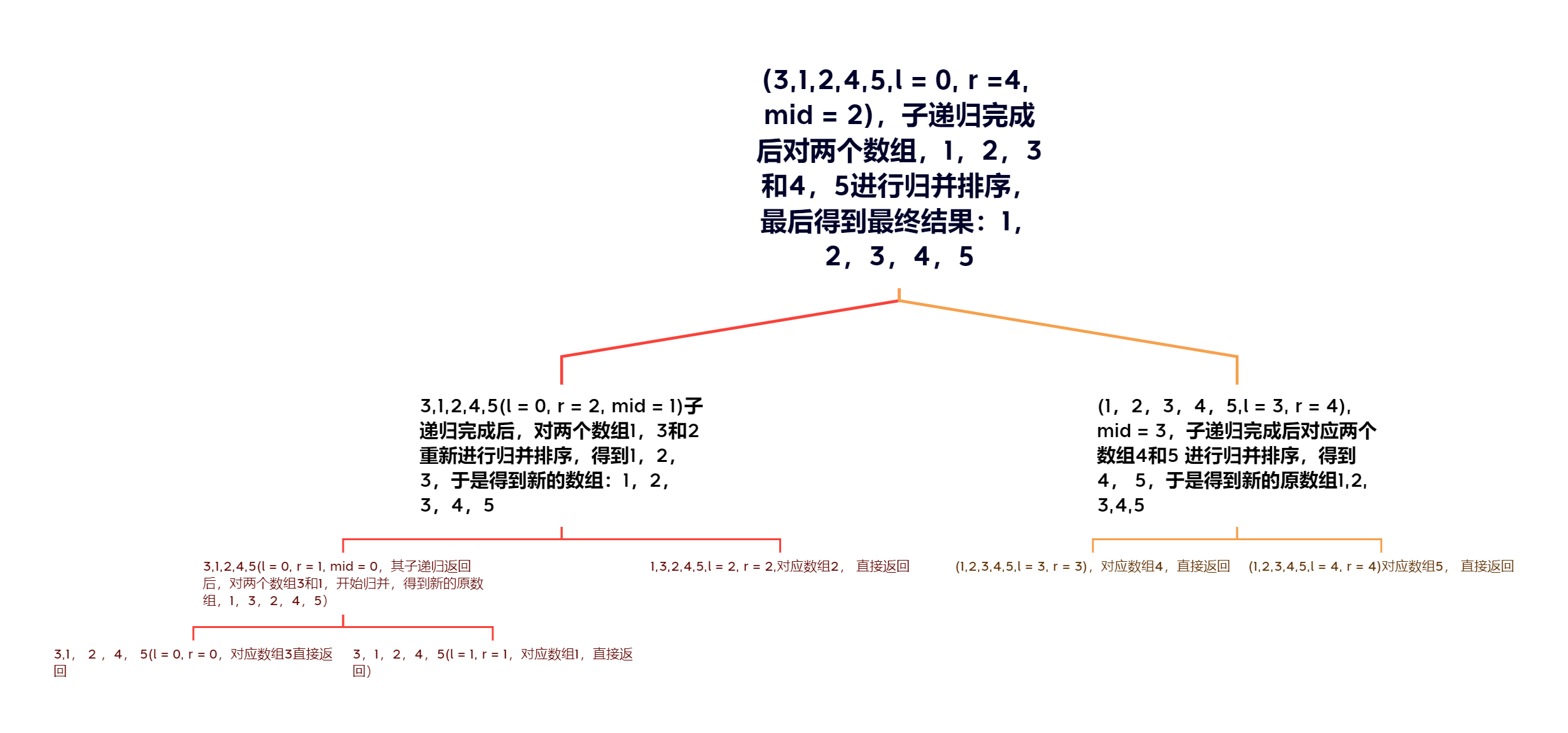
递归过程分析
以3 1 2 4 5为例,先看括号内的参数,再从叶子结点自底向上,自左向右分析
二分
整数二分
基本思想
整数二分的目的是:
取中间值mid,然后检查mid的性质,来找到一组数据中具有不同性质的两组数据的临界点
以二分查找为例:
取的中间值就是mid, 我们要找的数是x 那么这个数组中就具有<x以及>=x两种性质,我们通过检查mid的性质:其其为下标的数组元素是否<x或者是否>=x,来找到这两种性质的分界点x,最后返回的结果是分界点的下标
代码实现
bool check(int x){
/*....*/
}//检查x是否满足某种性质
//区间[l, r]被划分为[l, mid - 1]和[mid, r]时使用
//l, r是寻找区间的两个端点
int bearch_1(int l, int r){
while(l < r){
int mid = l + r + 1 >>1;
if(check(mid)){
l = mid;
}else{
r = mid -1;
}
}
return l;
}
//区间[l, r]被划分为[l, mid]和[mid + 1, r]时使用
int bearch_2(int l, int r){
while(l < r){
int mid = l + r >> 1;
if(check(mid)) r = mid;
else l = mid + 1;
}
return l;
}
代码理解
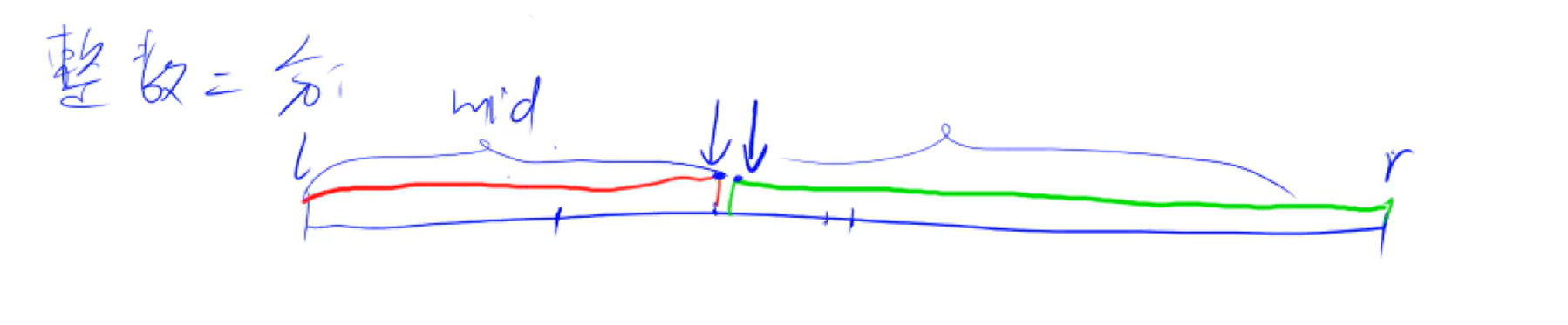
红色和绿色分别代表两种性质,在二分查找中 ,红色代表小于x,绿色代表大于等于x
注意:
- 走出循环的时候一定是
l = r,因为是一点点减一的 - 这一堆数据中的不同性质的临界点必为两个,我们要根据情况来使用不同的模板来查找,比如在二分查找中,
<x这种性质的分界点是小于x的最大数,>=x这种性质的分界点是>=x的最小数,所以我们使用二分查找的模板就是去寻找右边性质的临界点 - 找左边的临界点的时候是用模板二,找右边临界点的时候是用模板一
- 使用模板一的时候,也就是找左边临界点的时候,由于c语言的出发舍入规则,必须把
mid设置为l + r + 1>>2,比如就两个数,下标为0,1,l = 0, r = 1,mid = 0当进入循环的时候,若此时下标mid对应的数满足性质则变为l = 0, r = 1,mid = 0进入死循环 - 二分模板是一定可以找到结果的,比如二分查找,哪怕具有
>=x的性质中没有数x,我们的模板仍然会找到这个性质的临界点: 大于等于x的最小值,至于这个值正不正确是由题目决定的,与我们的模板无关 - 做题的时候先写
check(mid)然后再看自己找的是做临界点还是右临界点,若是左临界点,则mid = l + r + 1 >> 2 - 哪怕在右边的性质中的边界点是两个,比如右边的性质是大于等于x,但是数组中有两个x,但是最后的结果仍然是找到边界点,比如数组
1 2 2 3 3 4,右边的性质是大于等于3,我们用二分来找右边的临界点,找到的数的下标是3,是最左边3
浮点数二分
基本思想
与整数二分类似,不过由于浮点数是连续的,所以边界点就只有一个,所以也就一个模板
代码实现
bool check(double x){
/*.....*/
//检查x是否满足某种条件
}
double bsearch_3(double l, double r){
const double eps = 1e-6;//eps表示精度,取决于题目对精度的要求
while(r - l > eps){
double mid = (r + l) / 2;
if(check(mid)){
r = mid;
}else{
l = mid;
}
}
return l;
}
代码理解
- 浮点数二分只有一个边界点,每次取
mid的时候都是准确取值,精准二分 check(mid)若满足红色性质,则r = mid,若满足绿色性质则l = mid
高精度
基本思想
- 一般而言,大整数的位数是106级别
- 大整数的存储,数的每一位存到数组里面去,且数组的第0位存数个位,因为如果结果有进位的话,直接在高位,也就是数组末尾增加一位要比在数组的开始增加一位方便
加法
基本思想
- 从个位开始往前算
- 对于每一位,两个数对应的位相加并加上上一位的进位,若大于十则进一,否则不进一,
Ai + Bi + t
代码实现
#include<iostream>
#include<vector>
using namespace std;
const int N = 1e6 + 10;
vector<int> add(vector<int> &A, vector<int> &B){
vector<int> C;
int t = 0;//作为进位,以及中间结果
//简化代码,不用区分A和B谁的位数大,注意相加有进位的情况,AB,位数相加结束,但是不能退出循环,要处理进位
for(int i = 0; i < A.size() || i <B.size() || t != 0; i++){
if(i < A.size()) t += A[i];//t作为中间结果
if(i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;//t作为进位
}
}
int main(){
string a, b;
vector<int> A, B;
//用字符串读入两个整数
cin >> a >> b;
//假如a=123456
//将a存入数组A中
for(int i = a.size() - 1; i >= 0; i--){
A.push_back(a[i] - '0');//A中是654321
}
for(int i = b.size() - 1; i >= 0; i--){
B.push_back(b[i] - '0');
}
//auto自动判断C的类型
auto C = add(A, B);
for(int i = C.size(); i >= 0; i--){
cout<<C[i];
}
return 0;
}
减法
基本思想
- 对于每一位先计算
Ai - Bi - t,t是上一位的借位,若大于等于0,则结果不变;若小于0,则结果为Ai - Bi - t + 10,并向上一位借一位 - 保证大整数A大于等于B,若A小于B,则交换总是算大数减小数,保证模板的最高位不会向前借位,然后加上负号
- 这里保证A与B都是正数
代码实现
# include<iostream>
# include<vector>
using namespace std;
const int 100010;
//判断A与B的大小
bool cmp(vector<int> &A, vector<int> &B){
//A与B的位数不相等的情况
if(A.size() != B.size()){
return A.size() > B.size();
}
//A与B的位数相等的情况,从最高位开始比较
for(int i = A.size() - 1; i >= 0; i--){
if(A[i] != B[i]){
return A[i] > B[i];
}
}
//A = B
return true;
}
vector<int> sub(vector<int> &A, vector<int> &B){
vector<int> C;
//t作为中间变量以及向前的借位
//保证A一定大于B
for(int i = 0,t = 0; i < A.size(); i++){
t = A[i] - t;
//如果B还有位可以减则减去B,否则不减
if(i < B.size()){
t -= B[i];
}
//(t + 10) % 10包含了两种情况,若是负数则需要加10,若是正数则结果必不大于10,加10再对十取余刚好把10去掉
C.push_back((t + 10) % 10)
//此时t再作为向前的借位
if(t < 0){
t = 1;
}else{
t = 0;
}
}
//去掉前导0,由于是减法,高位相减结果为0的时候也会导入C中(比如111-110,结果是001,此时需要去掉前面的两个0
//C是单个0的时候不去掉这个0,当C的位数大于1并且C的最高位为0的时候就要将这个0去掉
while(C.size() > 1 && C.back() == 0){
C.pop_back();
}
}
int main(){
string a, b;
vector<int> A, B;
cin >> a >> b;
for(int i = a.size()-1; i >= 0; i--){
//注意存进去的是数字
A.push_back(a[i]-'0');
}
for(int i = b.size()-1 i >= 0; i--){
B.push_back(b[i]-'0');
}
if(cmp(A,B)){
auto C = sub(A, B);
for(int i = C.size()-1; i >= 0; i--){
printf("%d", C[i]);
}
}else{
printf("-");
for(int i = C.size()-1; i >= 0; i--){
printf("%d", C[i]);
}
}
return 0;
}
乘法
基本思想
-
运算的对象是一个大整数A与一个正常的整数b
-
从个位出发,Ci=(Ai∗b+ti) ,ti+1=(Ai∗b+ti)/10,ti是上一位向这一位的进位,ti+1是这一位向下一位的进位
代码实现
#include<iostream>
#include<vector>
using namespace std;
vector<int> mul(vector<int> &A, int &b){
vector<int> C;
int t = 0;
//注意从个位开始计算
for(int i = 0; i <= A.size() ; i++){
t = A[i]*b + t;
C.push_back(t % 10);
t /= 10;
}
//当最高位进位不为0的时候仍然需要处理t
while(t){
C.push_back(t % 10);
t /= 10;
}
//去掉前导0,1111*0的情况
while(C.size() > 1 && C.back() == 0){
C.pop_back();
}
return C;
}
int main(){
string a;
int b;
cin >> a >> b;
vector<int> A;
for(int i = a.size() - 1; i >= 0; i--){
A.push_back(a[i] - '0');
}
auto C = mul(A, b);
for(int i = C.size() - 1; i >= 0; i--){
printf("%d", C[i]);
}
return 0;
}
除法
基本思想
- 除法仍然是一个大整数除以一个正常整数,求得得商是C,余数是r
- 除法是从最高位开始算,但是仍然是从最低位开始存
- 对于A得第
i位Ai,先是前面得到得余数r*10,然后加上Ai得到中间值,这个中间值再除以b得到的商作为结果的商的一位,得到的余数作为下一位的余数,一直到Ai处理完,得到的商其实是正常存放在结果中的,所以需要reverse一下,不需要反序输出,但需要处理前导0 - 最开始的时候r = 0, A的第一位A1,中间值为r * 10 + A1,然后除以b的商作为结果的商的第一位,余数作为下一位的余数
代码实现
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
vector<int> div(vector<int> &A, int b, int &r){
r = 0;
//r同时作为余数和中间结果
for(int i = A.size() - 1; i >= 0; i--){
r = r*10 + A[i];//r作为中间结果
C.push_back(r / b);
r %= b;//r再作为下一位的余数
}
//reverse函数将C反转一下
reverse(C.begin(), C.end());
//去掉前导0
while(C.size() > 1 && C.back() == 0){
C.pop_back();
}
return C;
}
int main(){
string a;
int b;
cin >> a >> b;
vector<int> A;
for(int i = a.size() - 1; i >= 0; i--){
A.push_back(a[i]-'0');
}
int r;
auto C = div(A, b, r);
for(int i = C.size() - 1; i >= 0; i--){
printf("%d", C[i]);
}
cout << endl;
cout << r;
return 0;
}


兄弟加油,每天晚上不看你的都睡不着觉