最近好好研究了一下y总 @yxc 提出的闫氏dp分析法
理解了好半天，归根结底可能是和各位大佬
比如和 @垫底抽风 等等，比起来，自己太菜了，智商捉急
又对该方法进行了细致的分析，改善
不需要很高的智商，也能慢慢理解
于是写了这个长篇大论
闫氏dp分析法，给予了dp问题一个状态集合的框架
但是有时候处理复杂dp问题，更多时候依靠的是经验

当你拿到“闫氏dp分析法”框架，和dp问题的时候
具体应该怎么样展开思考过程呢？
我这里给出了一些更为细致化的思考

闫氏dp分析法

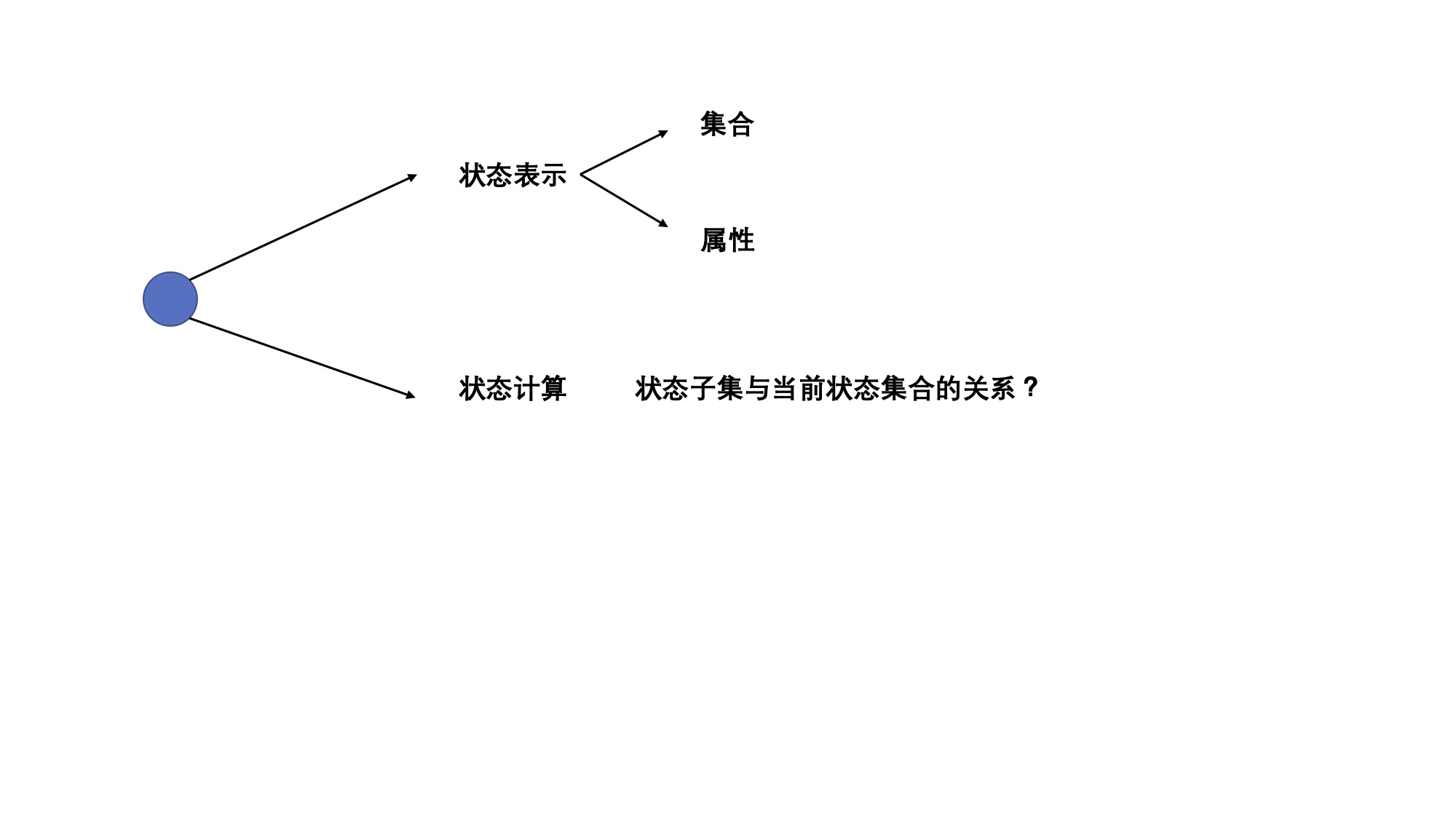
其中属性，一般很容易搞定
一般情况下，属性是题目要求我们求啥，它就是啥

那么，集合的确定，以及状态计算，该如何展开思考？
这里做一点细致的补充

集合的确定

第一步，确定dp的阶段

dp的阶段，必须取独立变量
什么意思呢？这个可以类比成概率统计中的独立随机实验
概率统计中的独立性什么意思呢？独立实验，就是两次实验的结果，是独立的
一次实验的结果，并不会影响另一次
同样，这里的dp阶段，也必须遵循这个原则

$\{第 \ i \ 阶段的属性 \ d(i) \}$ 与 $\{第 \ i+1 \ 阶段的属性 \ d(i+1)\}$
相对独立

简单粗暴点，也就是说第 $i$ 阶段，我爱选谁选谁
第 $i+1$ 阶段，我也可以爱选谁选谁，不会受到第 $i$ 阶段影响

注意，这里的独立，指的是结果不相互影响，也就是dp中的无后效性
但二者必须存在某种联系，对于线性dp问题

$$ d(i+1) = d(i)+ f(i) \\\ \\ \\\ f(i) \textbf{ 可以是线性表达式，或者是 } \min or \max $$

这样讲比较抽象，下面给出一个依葫芦画瓢的过程，具体的方法！

重点！！！！
列出题目中所有的变量，分析那些变量有相对独立关系？

来看几个例子

传纸条
列出问题中所有的变量，我们发现

$\text{坐标是变化的}， (x, y) \text{能否作为 } dp \ 的阶段？$
答案是不行，为什么呢？因为题目中要求是找到 2 条路径！
如果两条路径都经过 $(x, y)$，而一条路径如果取走$(x, y)$
中的数，直接影响到了第二条！这就违背了独立性，因为你决策$(x, y)$
产生的结果，直接影响了下一次决策
但是还可以补救，要想保持独立性，怎么办？
我们需要再加一个维度 $(x, y, flag)$，用 $flag = [0, 1]$ 来记录当前这个坐标，属于第一条路径，还是第二条？
不过这样，增加维度，只会使得后面状态计算更加麻烦

$\textbf{还有什么是变化的呢？注意到这里一次，只能走一步}$
$\textbf{所以用步数 } i \text{ 作为 }dp \text{ 的阶段，可以吗？}$
步数是相对独立的，为什么呢？
$\text{因为你第 }i \text{ 次取数，第 } i+1\text{ 次取数，是互相不影响的}$
不管你第 i 次取多少，你第 i+1 次都必须重新取数，重新走
这就是独立性

确定dp阶段之后，就可以进入下一步分析了，不过这里还想再多讲几个例子

I-Country
有了上面的经验，这个dp的阶段选择，其实就相对直观了
用行或者列作为dp的阶段
$i \in [1, N], j \in [1, M]$ 都可以作为 dp 的阶段
无非就是当前遍历到第 $i$ 阶段的时候，发现已经选择了 $K$ 个格子了
我们就更新ans，并不会影响到第 $i+1$ 阶段，第 $i+1$ 阶段我们也是如此，
检查，然后更新ans，这就具有了独立性

饼干
这个题目也是属于经典问题了
不过这里重点思考一下，发现

第 i 个孩子分到饼干，影不影响第 i+1 个孩子?
注意到如果饼干拿到的多，或者少，会影响到
$d(i+1) = d(i) + f(i)$
$f(i)$ 会产生一个怨气值，但注意，这里不叫影响
这个是第 i 个孩子拿饼干和第 i+1 个孩子那饼干的状态转移
第 i 个孩子拿饼干，是和第 i+1 个孩子拿到饼干的过程相对独立
也就是说，第 i 个孩子能拿到饼干，并不会对第 i+1 个孩子拿到饼干产生影响
第 i+1 个孩子该拿拿，不该拿就不拿，和第 i 个孩子无关
$i \in [1, n] \text{ 可以作为 dp 的阶段}$

再看饼干，假设当前分配了 j 个饼干，对分配 j+1 个饼干有没有影响？
也是没有的，第 j+1 个饼干爱怎么分配怎么分配，爱给谁就给谁

$d(i, j) $ 孩子，和饼干，都可以作为dp的阶段

类似的问题还有啥？
还有公共子序列问题啊！
$A[i], B[j]$
在公共子序列选择 $A_i$， 对 $A_{i+1}$ 不会造成影响
同样，选择 $B_j$ 对 $B_{j+1}$ 也不会造成影响
都是你爱选就选，不选就拉倒

饼干问题特殊性的说明

饼干这个问题有点特殊，因为
$f(i) = g(i) \cdot a(i)$
$a(i)$ 取决于相对顺序
取决于相对顺序的问题，一般情况下都有等效冗余
什么意思呢？

$a_{i} = f(\Delta x_i), \quad \Delta x_i = x_i - x_{i-1}$
我把 $x_i, x_{i-1}$ 都减掉 $t$，
$\Delta x_i = (x_i - t) - (x_{i-1} - t)$ 结果是完全不变的
当然前提是 $\textbf{for } \forall i , \quad x_i -t > 0$
也就是说，这个问题的等效状态是

$d(i, j): \textbf{for }\forall i, \quad x_i = x_i - t, \quad (x_i > t)$

$d(i, j) \Leftrightarrow d(i, j - \sum(t))$
$\textbf{你每个人都少拿 t 个饼干，总的饼干就少拿 } j - \sum(t)$
类似的思想，我写过一篇博文，叫做差分dp
差分dp

那好了，经过上面的分析
这个 $t$ 的取值，会对 $ans $ 产生影响吧？
$t = [1, 2, \cdots]$
其中，$t = 2$ 又可以由 $t = 1$ 这个阶段递推而来
$t = 3$ 由 $t = 2$ 这个阶段递推而来
很幸运的是，我们又发现了新的 dp “阶段” 了

这就是为什么饼干这道题目，在最后的状态转移方程递推中
$f(i, j) = f(i, 1\cdot (j-i))$
我们每次只拿走 $t$ 个饼干，保持 $\forall i, \ x_i - t > 0$
便于后面的状态转移

还有其他的例子，我再仔细说说

最优配对问题

空间里有 $n$ 个点 $P_0, P_1, \cdots, P_{n-1}$
将他们配对成 $\frac{n}{2}$ 对，使得每个点恰好在一个点对中
所有点对中的两点距离之和尽量小

这个问题中，显然应该把点作为 dp 的阶段
因为每个点 i 都可以爱和谁配对就和谁配对
不受第 i-1 个点的配对情况的影响
先写出状态转移方程
以配对的点作为 $dp$ 的阶段
当前已经配对了 $i-1$ 个点，正在配对第 $i$ 个点

可以用状态压缩的方法，当前点在不在集合 $S$ 中，可以用二进制表示

$$ d(i, S) \xleftarrow{\min} d(i-1, S-\{i\}-\{j\})+ |P_iP_j| \\\ \\ \\\ d(i, S) = \min_{j \in [0, i-1]} \{|P_iP_j|+d(i-1, S-\{i\}-\{j\})\} $$

图的色数

给一个无向图 $G$，把图中的节点染成尽量少的颜色，使得相邻节点的颜色不同

这个问题，能不能把节点作为 dp 的阶段？
显然是不行的
第 $i$ 个节点能爱涂什么颜色就涂什么颜色吗？！
它取决于相邻的节点颜色的影响！

那么什么可以作为dp的阶段呢？
这个问题还有什么变量？对！颜色数
当前涂第 $i$ 号颜色，我们原则上是能够爱涂什么节点涂什么节点的
但是，要求颜色数最少，根据贪心策略，我们要把能涂 $i$ 号颜色的点
全部都涂上 $i$ 号颜色
这样，第 $i+1$ 号颜色涂色的时候，和第 $i$ 号颜色就无关了

用当前已经在集合 $S$ 中的节点数作为 $dp$ 的阶段
$d(S)$ 表示当前节点集 $S$ 最少用了多少种颜色？

$\exists S’ \subseteq S, S’$ 是可以染成同一种颜色的节点集
根据条件，$S’$ 必然是个独立点集，$S’$ 中的节点没有边相连

$$ color\{S-S’\} + color(S’) \\\ \\ \\\ d(S) = \min\{d(S-S’) + 1\} $$

消木块
这个是经典的区间 $dp$ 问题
对区间 $[l_1, r_1]$ 执行方块消除，并不会影响区间
$[l_2, r_2]$ 的执行

所以可以用区间dp解决
但是这里有一个问题，就是仅仅用 $[l_1, r_1]$ 没有办法囊括所有的状态
$[l, r]$ 之后，从 $[r+1, \cdots]$ 可能还会有一部分残余
而这些残余本来应该和 $[l, r]$ 连带消除
状态定义看这里

重点！！！
当用当前阶段的维度，不足以囊括所有状态的时候，考虑增加维度

这里我们用 $f(l, r, k)$ 表示 连带消除 $[l,r]$
之后长度为$k$ 的方块段

棋盘分割

这个问题的阶段划分，有两个
区间范围 $\textbf{or}$ 当前已经切了第几刀？

第 k 刀，也是爱怎么切就怎么切，和第 k-1 刀无关
切第几刀，这个变量是相对独立的
但问题是，仅仅用第几刀，能不能完全囊括状态？？
这取决于横着切，竖着切，斜着切，蛇形切，各种切，对答案会不会产生影响？
如果会，那么要加维度

$dp(k, flag), \quad flag=[\text{横着切，斜着切，}\cdots]$
如果发现加了维度之后，状态转移困难的话
就考虑其他变量作为 dp 的阶段
本例中还有啥变量？对啊，区间嘛

$[x_1, x_2], [y_1, y_2]$也可以作为dp的阶段

好了，好累啊，休息一下
为什么写这篇文章呢？因为我自己发现
我智商比较低下，很多时候面对 dp 问题的时候
不知道别人怎么能想到这样做，而我却想不到
话不多说，休息一下，继续讲第二部分

第二步，根据dp的阶段，不重复，不遗漏地描述各个阶段状态

这个问题，有了第一步的铺垫，反而比较好理解

消木块
前面讲了，消木块这个问题，只用 $[l, r]$ 是无法囊括全部的状态的
为什么呢？

因为$[l, r]$ 之后可能 $[r+1, \cdots]$ 连续一段，它的颜色
和 $A[r]$ 相同，本来之后的这一段应该要连带消除的
但是呢？仅用 $[l, r]$ 并不能把这个操作信息给描述出来
所以需要增加维度
$f(l, r, k)$ 表示消去区间 $[l, r]$ 并且连带消除之后的长度为 $k$ 的段

最优配对问题
前面讲过，最优配对问题用当前配对的第 $i$ 个点作为dp阶段
空间里有 $n$ 个点 $P_0, P_1, \cdots, P_{n-1}$
将他们配对成 $\frac{n}{2}$ 对，使得每个点恰好在一个点对中
所有点对中的两点距离之和尽量小

$d(i)$ 表示当前正在配对第 $i$ 个点，$[1,\cdots, i-1]$ 已经配对完成了
此时的点对距离之和的最小值

那么仅仅凭借 $d(i)$ 能完全描述状态吗？
如果当凭借 $d(i)$，我们并不能够知道 $i$ 这个点和谁配对
我们还需要增加一个维度，来描述已经配对的点的集合

重点！！
增加状态维度，来不重复，不遗漏地描绘各个阶段状态
方法有2种

第一种，增加维度，这个维度是一个点, 比如这里我们可以用
$d(i, j)$ 描述已经在集合中的元素 $j$，让 $(i, j)$ 配对
这种方法比较麻烦，可以用 STL 的 set 来维护已经配对的点的集合
$\textbf{for }\forall j \in [1, i-1]$
$\quad \textbf{if } node[j] \in \{set\}, \text{配对 i, j}$
当然用 $vis[j]$ 来描述这个点在不在集合中也是可以的

第二种，状态压缩，把集合 $S$ 看作一个整体
因为每个点都只有在或不在2种可能
这里可以用一个 $n$ 位的二进制数来描述 $S$

if(S & (1<<j))
    j这个点就在集合中
    尝试配对 (i, j)
    把 i 加入集合
    S |= (1<<i)

如果 n 不大，建议用状态压缩
状态压缩中，加入/剔除某个元素的操作也很简单

S |= (1<<i)
    加入元素
S ^= (1<<i)
    剔除元素

重点！！！
第二步，最关键的，就是根据 dp 的阶段
不重复，不遗漏地描述当前阶段所有的状态
如果不能完全描述状态，考虑增加 dp 维度
但是一般来说，增加的维度要尽量少！
这样一是便于我们下一步写状态转移方程
另外也可以降低时间复杂度

状态计算

其实我觉得难点还是第一部分，集合的划分
状态计算相对简单
这一步要做的是，写出状态转移方程

$$ d(i, \cdots) = d(i-1, \cdots) + \{f(i, S)\} $$

首先，我们认为第 $i-1$ 阶段的 $d(i-1, \cdots)$
是已经算出来了！

此时，状态集合 $S$ 包括了 $[1, \cdots, i-1]$
所有阶段的目标决策, 这个目标决策和闫氏dp分析法中的属性
以及之前的集合定义有关，需要多做dp题目，把握感觉

那么，我们要做的是什么呢？我们需要做的其实是计算
$f(i, S)$
重点！！！
计算把当前阶段 $i$ 加入决策集合 $S$ 所产生的代价$f(i, S)$
一般来说，这里的 $f(i, S)$ 都是分段函数

$f(i, S) = \begin{cases} calculate(i, 1) && \text{1} \\\ calculate(i, 2) && \text{2} \\\ \cdots \\\ calculate(i, i-1) && \text{i-1} \end{cases}$

这个时候，$i$ 加入决策集合，可能跟 $j \in [1, i-1]$ 中的一个，或者几个，配对，产生代价
常见的代价可以是
$dist(i, j), \max(i,j), \textbf{count}(i), \cdots$

比如距离，点的计数，最大，最小值等等
常见的代码模版是

普通集合

for i = 1 to n
    for j = elements in [S]
        d(i, ...) = max(d(i-1, ...) + dist(i, j))
        d(i, ...) = d(i-1, ...) + [count(i) = 1]
        d(i, ...) = d(i-1, ...) + cost(i, j)

状态压缩集合

for i = 1 to n
    for S0 = S; S0; S0 = (S0-1) & S
    // 也就是说枚举 S 的所有子集
    if(S0 & state[i], S0 & (1<<i), ...)
        j = S0 & state[i];
        d(i, S) = d(i-1, S0) + cost(i, j)

诸如此类

这个时候，$i$ 加入决策集合，可能跟 $j \in [1 \cdots i-1]$ 中的一个，或者几个，配对，产生代价
这个配对的过程，也就是状态 $j$ 向状态 $i$ 进行状态转移过程

最后，根据状态转移方程，确定初始状态和结束状态

到了这一步，马上就大功告成了！

用 st 表示起始状态 (其实就是start简写)
用 ed 表示目标状态 (end的简写)

这个根据状态转移方程，和第一步集合的定义，很容易得出

根据个人习惯，有的人做dp喜欢用dfs递归+记忆化
有的人做dp喜欢用数组递推

dfs加记忆化模版

initdp() {
    memset(d, -1, sizeof(d))
    // -1 表示这个点还没有计算，这个在记忆化中比较常见

    d[ed] = {0, infinity, ...balabala}
    // 一般情况下，如果用记忆化
    // 必须在开始先确定目标状态
    // 由目标状态反着推到起始状态
}

int dp(int i, int S) {
    if(S == ed) return ans;
    // ans 一般这里是 d[ed];

    if(d[i] >= 0) return d[i];
    // 记忆化

    for j = elements in [S]
        dp(i, S) = dp(i+1, S') + cost(i, j)
        // 记忆化搜索+dfs一般都是反着推
        // 从第 n 个阶段反着推到 i
}

int main() {
    initdp();
    dp(0, st);
}

递推模版

initdp() {
    memset(d, 0, sizeof(d));

    d[st] = {0, infinity, ..., balabala}
}

void dp() {
    for(int i = 1; i <= n; i++) {
        for j = elements in [S']
            S' 加入 i 元素之后变成集合 S
            d(i, S) = d(j, S') + cost(i, j)

            有时候，d(i, S) 也仅仅与 i-1 这个阶段有关

        sometimes, may be
        d(i, S) = d(i-1, S') + cost(i)
    }
}

int main() {
    initdp();
    dp();

    ans = d[ed];
}

好了，我打字好累啊
接下来会写一下有后效性的
和单调队列优化，斜率优化等等乱七八糟的