匈牙利算法

注，为了防止各位单身狗们产生一些不适症状，本期分享并不会撒狗粮，汪汪汪

以及今天没太有时间，不录视频了。

请大家放心观看！

一。匈牙利算法是干什么的

匈牙利算法是用来求二分图的最大匹配的。

那神马是二分图的最大匹配？

这里我们用上衣和裤子搭配举例子。
二分图的最大匹配就是你把所有的上衣和裤子匹配成一套完整的衣服，
能匹配的最大组数。
注意一件上衣&裤子不能重复匹配
匈牙利算法就解决了这样一个问题。
转化成图论里的外星人话就是：

二分图的匹配：给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个> 匹配。

二分图的最大匹配：所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配，其边数即为最大匹配数。

所以匈牙利算法要有一个形象的例子
y总的栗子是谈恋爱
因为不能撒狗粮所以就这么将就着吧……
wtcl

好了现在正式开始讲解。
首先我们来把图画下来。
青色的线表示可以进行匹配。

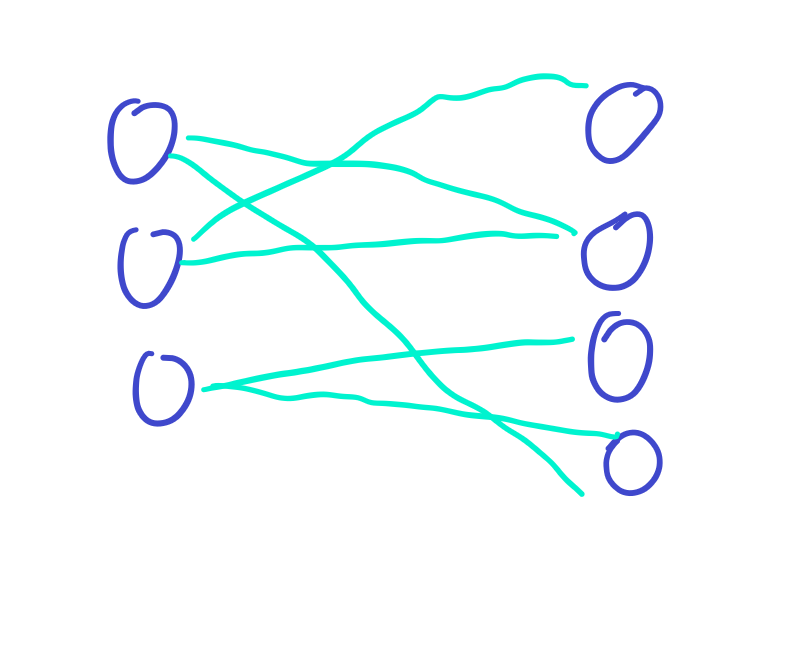
首先我们从上衣开始遍历。
首先上衣1可以连接裤子2。
那我们就连接上。

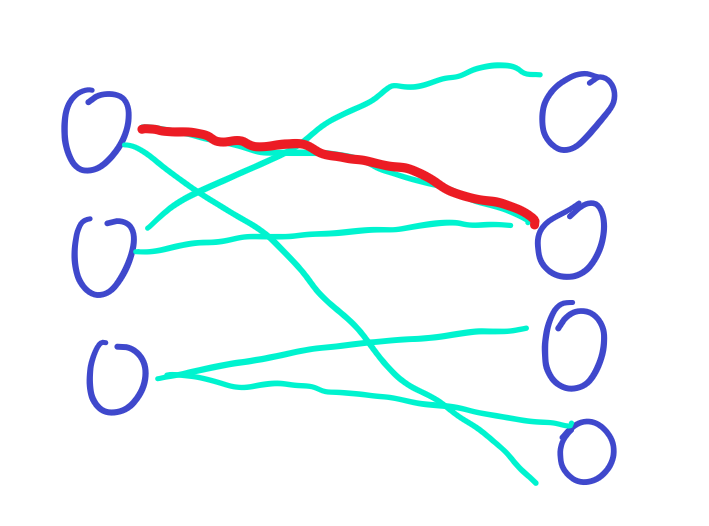
接下来遍历第二个上衣。
一直遍历下去，我就刚刚好可以匹配上所有的衣服。
但如果发生特殊情况呢？

请看下图。

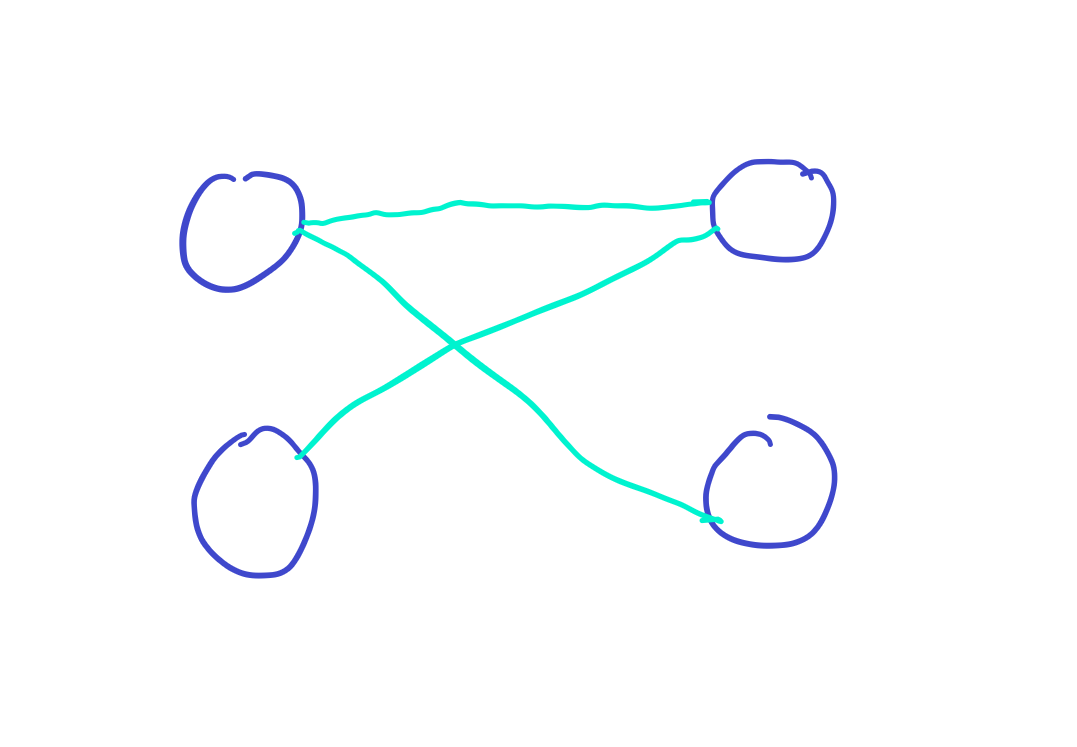
首先匹配第一个上衣和裤子，匹配成功。

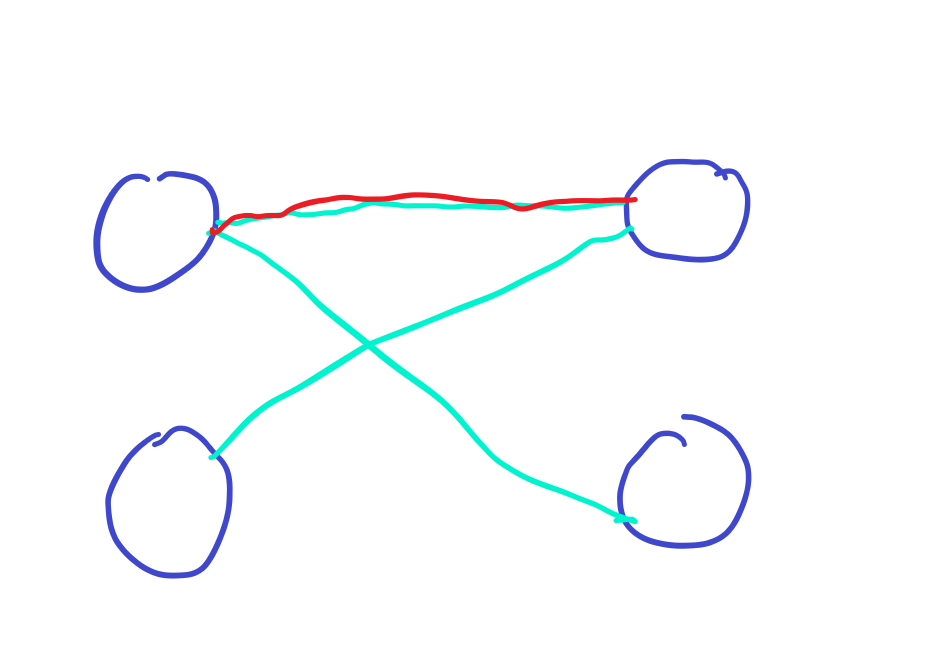
接着尴尬的一幕发生了，
第二个上衣没法匹配了！

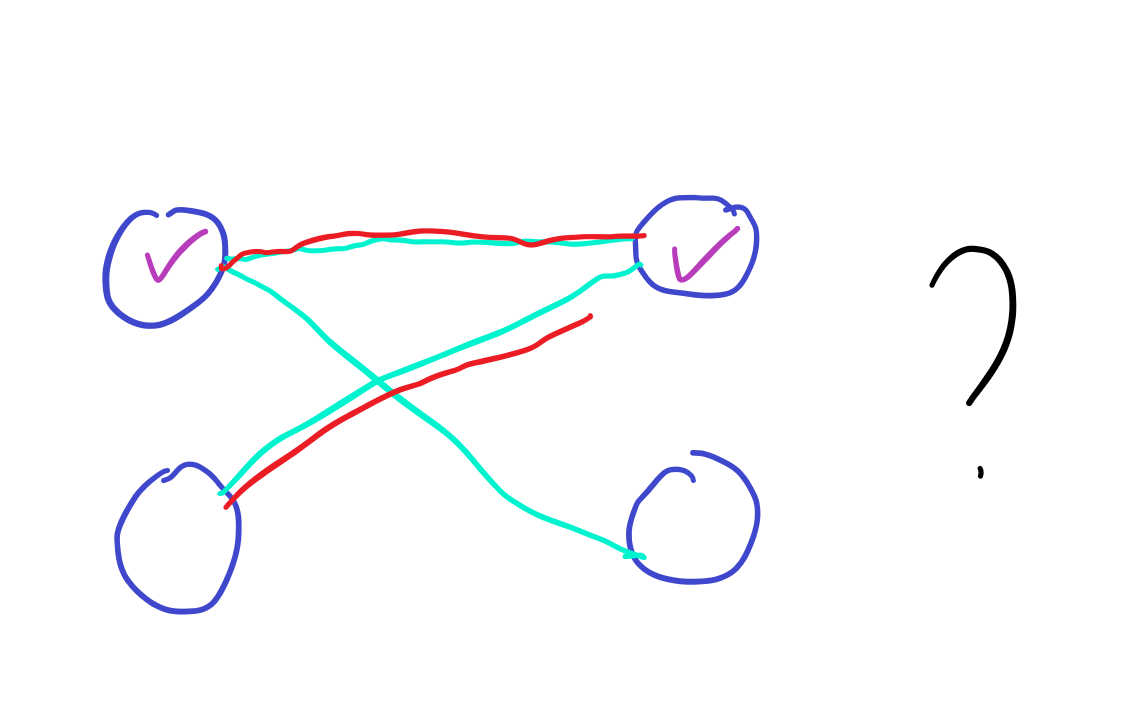
那我们应该怎么办呢？
我们可以把第一个上衣和第二个裤子匹配。
这样第二个上衣就可以匹配了。
一般这条断开的线，是绿的

绿色是真实的颜色——yxc

这就是匈牙利算法的匹配过程。
接下来是证明。

前方高能！

注，以下证明转载自梦之泪殇的一篇blog

总共分为两个命题：
$ \left\\{ \begin{aligned} 命题1： & 在当前匹配下，没有搜索到增广链就说明该点不是最大匹配的必要点？或者说没有找到增广链，该匹配就是最大匹配？ \\\ 命题2： & 在目前的匹配情况下，没有搜索到以该点u_{k+1}开始的增广路径，在后面加入别的点的匹配情况下，也不可能有以该点开始的增广路径存在 \\\ \end{aligned} \right. $

以下是天花乱坠的证明过程：

定理：存在增广链是增广当前匹配的充要条件

等价的命题是，为什么在当前匹配下不存在以左边某一未匹配点开始的增广链，该点就不是当前匹配下增广的必要点，即该点不能增广当前匹配。

从匹配增广的原理可以看出，以该点开始的增广链是该点可以增广当前匹配的充分条件

必要条件？

首先能理解的是：如果增广路径从左边开始终止在左边点

路径上已经选择的边和没有被选择的边数量相同

按照前面介绍进行增广操作并不能增加比配边数

然后用反证法去证明如果该点能改善匹配，那么就一定存在，不需要改变原来匹配点集合的（已经匹配的点一定在改善后的匹配中），以该点开始的增广链

在这里假设已经匹配的左边点为，对应的右边点为

如果该点能改善匹配，那么根据匹配的独立性，必然在改善后的匹配中，右边也有个点，而且，只需要一个新的右边点加入匹配即可（这个可以从下面的分析中可以看出）

1.如果在改善的匹配中，匹配的是新点，那么就是一条增广链

2.如果匹配的不是新点，那么假设匹配的是，在原来匹配中匹配对象是，根据匹配唯一性，在改善后的匹配中匹配的肯定不是，如果匹配的是新点，那么就是一条增广链

3.如果匹配的还是原来匹配的点，那就继续上面的分析2，根据已经匹配点数量是有限的，当分析到最后一个左边点时，根据匹配的唯一性，它必然和新点连接（因为旧点只有k个），那么增广链依然存在（开始，结束，中间穿过所有的和）

综上分析，如果存在改善匹配包含了该新点，那么就必然存在一条以该点开始的增广链，而且新增的右边点仅仅有一个，不需要另外的点去替换原来的右边点

引理：那么根据存在增广链是增广当前匹配的充要条件，算法只要遍历所有未匹配的左边点，没有找到增广链，即可终止算法，找到最大匹配

另外一方面

定理：在目前的匹配情况下

没有搜索到以该点开始的增广路径

在后面加入别的点的匹配情况下，也不可能有以该点开始的增广路径存在

（这个保证了算法只要遍历一遍左边点即可，不需要重复遍历）

证明：

原来的匹配为，对应的右边点为

如果加入新点和时，所使用的增广链为，改善后的匹配变成和对应的，p=k+1

前提：在原来的匹配下没有增广路径

假设在改善后的匹配下存在增广路径

1、如果增广路径中不存在，  中的，那么增广路径肯定不存在，这是因为改善匹配中存在匹配，所以

中的和都是原匹配中的，因此这是原匹配中的一条增广路径，和前提相悖

2、如果增广路径中存在，  中的，那么原匹配中必然存在增广路径，也是原匹配中的一条增广路径，和前提相悖

综上即证
————————————————
版权声明：本文为CSDN博主「梦之泪殇」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_25379821/java/article/details/83721379

好继续。
我们来看一下题。
二分图的最大匹配

给定一个二分图，其中左半部包含n1个点（编号1~n1），右半部包含n2个点（编号1~n2），二分图共包含m条边。

数据保证任意一条边的两个端点都不可能在同一部分中。

请你求出二分图的最大匹配数。

二分图的匹配：给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个匹配。

二分图的最大匹配：所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配，其边数即为最大匹配数。

输入格式
第一行包含三个整数 n1、 n2 和 m。

接下来m行，每行包含两个整数u和v，表示左半部点集中的点u和右半部点集中的点v之间存在一条边。

输出格式
输出一个整数，表示二分图的最大匹配数。

数据范围

1≤n1,n2≤500,
1≤u≤n1,
1≤v≤n2,
1≤m≤105

输入样例：

2 2 4
1 1
1 2
2 1
2 2

输出样例：

2

本题就是求一个二分图的最大匹配。
讲题的同时顺便把代码落实一下。
首先我们需要处理读入，此题没有边权。
看数据范围可得出，本题适合用邻接表来存储图。
所以先写上。

const int N = 510, M = 100010;

int n1, n2, m, match[N], h[N], e[M], ne[M], idx;

bool st[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

来存储图。
接下来我们来想一下这道题最主要的部分——
find函数
find函数是求每个上衣所对应的裤子并标记。
如果不行返回false。
首先我们需要遍历一遍所有这个上衣可以匹配的裤子。

for(int i = h[x]; i != -1; i = ne[i])
{
    int j = e[i];

}

接着我们进行如下判断：
首先，这个点必须没有被遍历过。

if(!st[j])
{

}

然后我们看一下：
1. 如果没有被匹配，匹配成功
2. 如果已经被匹配，试着递推更改。

但在这些之前需要先标记这个点。

st[j] = true;
if(match[j] == 0 || find(match[j]))
{
    match[j] = x;
    return true;
}

最后如果不行返回false。

return false;

然后看一下这部分的完整代码。

bool find(int x)
{
    for(int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(!st[j])
        {
            st[j] = true;
            if(match[j] == 0 || find(match[j]))
            {
                match[j] = x;
                return true;
            }
        }
    }
    return false;
}

接着我们来想一下如何处理输出。
首先我们需要看一下每个点是否可以匹配，匹配边数++。
用res来存边数。
注意每次要清空st判重数组。
这里用memset就行了，在cstring库里。

int res = 0;
for(int i = 1; i <= n1; i ++)
{
    memset(st, false, sizeof st);
    if(find(i)) res ++;
}

最后输出一下。

cout << res << endl;
return 0;

这道题的完整代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 510, M = 100010;
int n1, n2, m, match[N], h[N], e[M], ne[M], idx;
bool st[N];
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
bool find(int x)
{
    for(int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(!st[j])
        {
            st[j] = true;
            if(match[j] == 0 || find(match[j]))
            {
                match[j] = x;
                return true;
            }
        }
    }
    return false;
}
int main()
{
    cin >> n1 >> n2 >> m;
    memset(h, -1, sizeof h);
    for(int i = 0; i < m; i ++)
    {
        int a,b;
        cin >> a >> b;
        add(a, b);
    }
    int res = 0;
    for(int i = 1; i <= n1; i ++)
    {
        memset(st, false, sizeof st);
        if(find(i)) res ++;
    }
    cout << res << endl;
    return 0;
}

好了这期分享就到这里了。

这是我的全部分享

下期再见。

bye~

以及7月11日凌晨12点前在线，会猛更分享哦（当然刷动森钓鱼大赛也在日程中）