B(区间求交集)
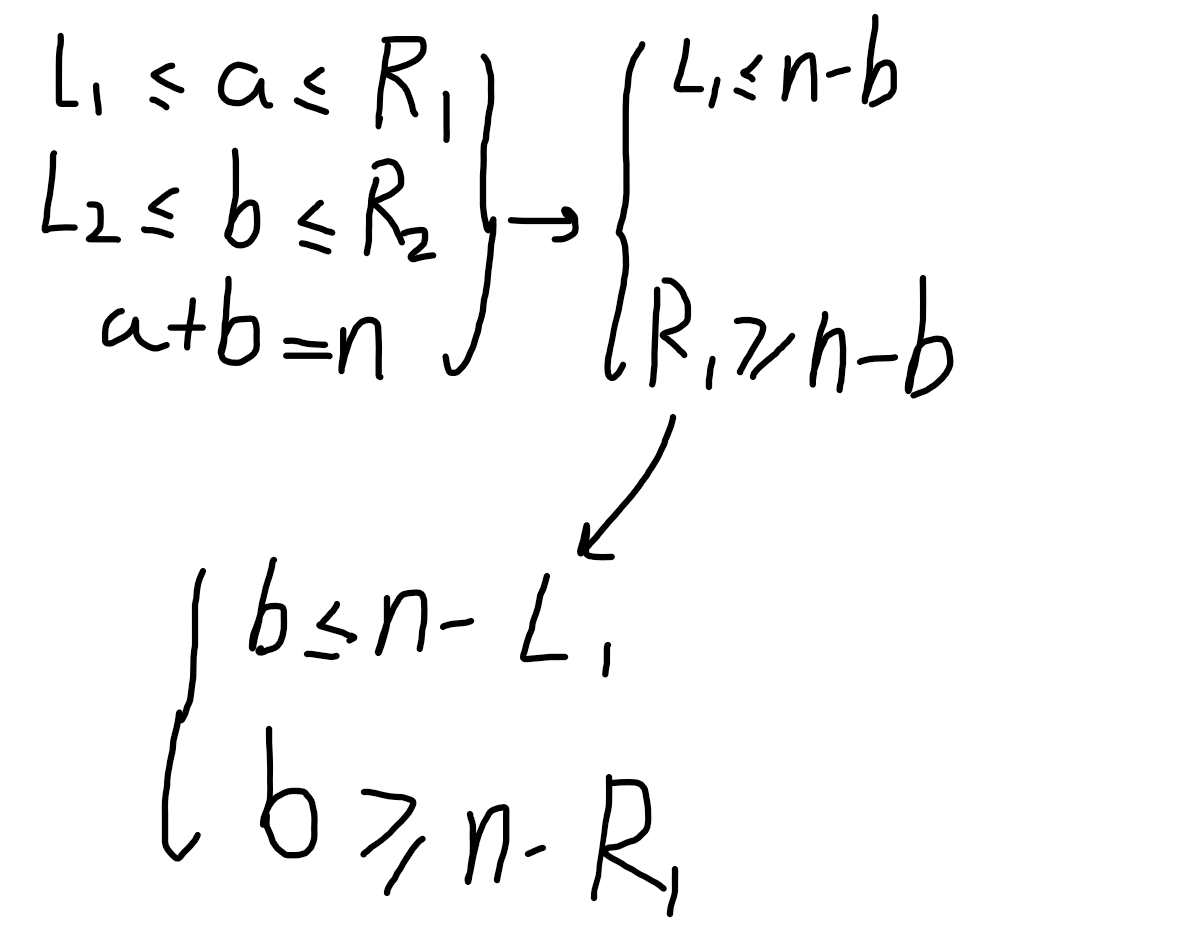
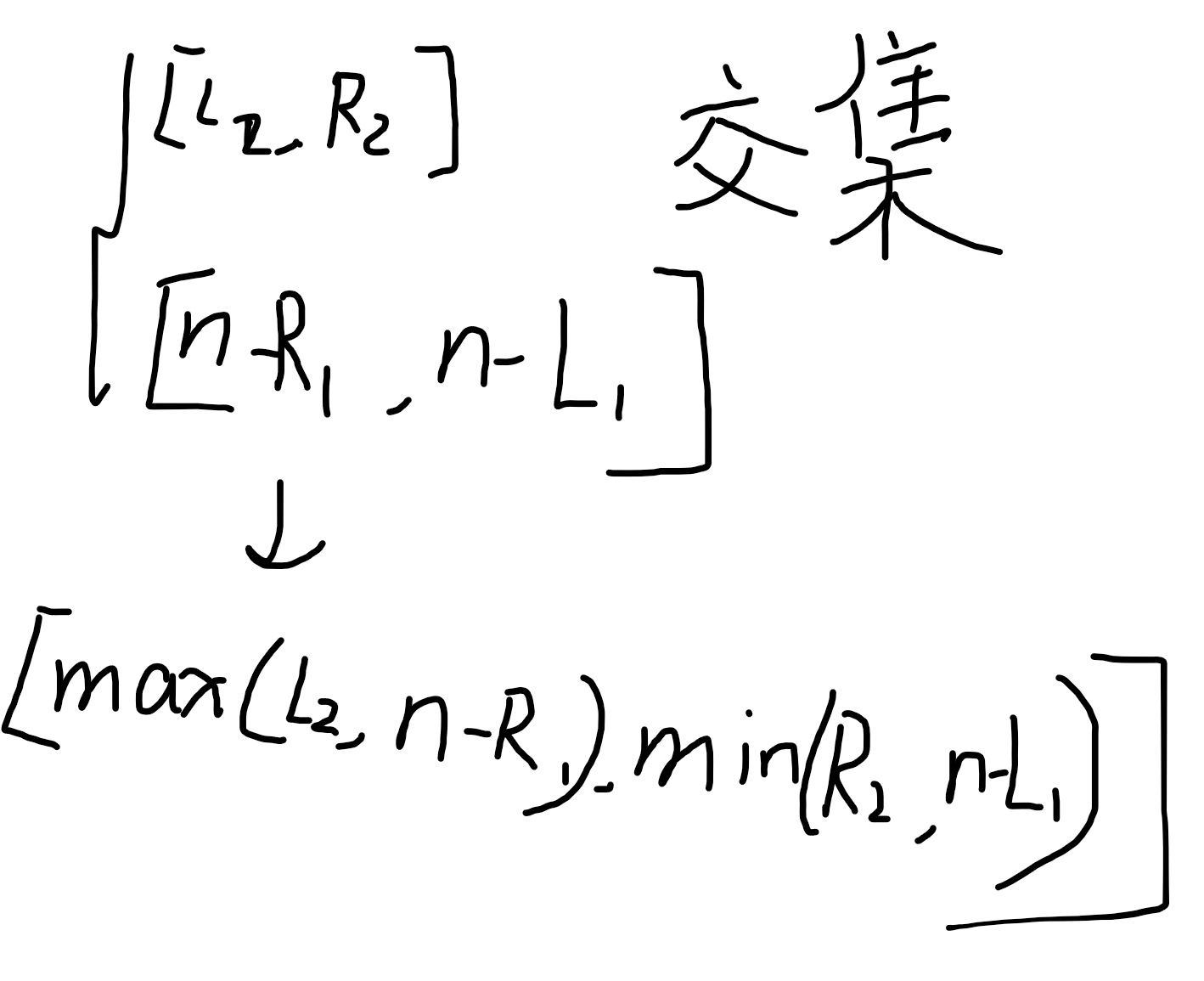
根据l2<=b<=r2和交集时候的公式可以找到答案,那么区间的交集也就是区间长度这时候就是答案了
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int a, b, n, a1, b1, a2,b2,sum,c,d;
int main()
{
int t;
cin >> t;
while (t--)
{
sum = 0;
int n;
cin >> n;
cin >> a1 >> b1 >> a2 >> b2;
ll aa=max(a2,n-b1),bb=min(b2,n-a1);
cout<<max(bb-aa+1,(ll)0)<<endl;
}
return 0;
}
J
推导公式

#include<bits/stdc++.h>
#define endl '\n'
using namespace std;
typedef long long LL;
LL a, b, n, m, sum, l, r, ll, rr;
int main()
{
int t;
scanf("%d", &t);
while (t--)
{
sum = 0;
cin>>n;
for (int i = 1; i <= n; i++)
{
cin >> l;
sum += abs(l);
}
cout << sum * 2 * n << endl;
}
return 0;
}
H
单独考虑算贡献
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int T,n,a[100010],c[100010];
int main()
{
cin>>T;
while(T--)
{
cin>>n;
memset(c,0,sizeof(c));
for(int i=1; i<=n; i++)
{
scanf("%d",&a[i]);//a[i]是存的数组
c[a[i]]++;//c[i]存的是出现的个数
}
multiset<int> st;//multiset<>可以存放重复的数
for(int i=1; i<=100000; i++)
{
st.insert(c[i]);
}
ll lesum=0,ge=((int)st.size());
for(int i=1; i<=n; i++)
{
//begin<=i,意思是当前的个数必须<=k
//if(begin()>k)则要放前k-1个
while(!st.empty()&&(*st.begin())<=i)
{
lesum+=(ll)(*st.begin());
st.erase(st.begin());
ge--;
}
printf("%lld\n",lesum+ge*(i-1));
}
}
return 0;
}
D
点积的形式,贪心
求深度可以使用并查集和dfs
#include<bits/stdc++.h>
#define endl '\n'
using namespace std;
typedef long long ll;
const int N = 2e5 + 10;
ll e[N], ne[N], idx, h[N];
ll num[N], a[N],p[N];
int main()
{
ll n;
cin >> n;
memset(h, -1, sizeof h);
for (int i = 2; i <= n; i++)
{
int x;
cin >> x;
p[i] = x;
}
for (int i = 1; i <= n; i++)
cin >> a[i];
for (int i = 1; i <= n; i++)
{
num[i] = num[p[i]] + 1;
}
sort(a + 1, a + n + 1);
sort(num + 1, num + n + 1);
long long sum = 0;
for (int i = 1; i <= n; i++)
{
sum += (long long)a[i] * num[i];
}
cout << sum << endl;
return 0;
}
L
预处理成(Ai*Aj)==x(modp)-Ak
1.先用两重循环算出每次重复2次的d数组
2.用c数组统计
3.枚举0~p-1分别输出答案(x-a[k]+p)%p是为防止负数
#include<bits/stdc++.h>
#define endl '\n'
using namespace std;
typedef long long ll;
ll p,n,c[5010],a[5010],d[5010][5010];
int main()
{
cin>>n>>p;
for(int i=1;i<=n;i++)
{
cin>>a[i];
a[i]%=p;
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(i==j)continue;
c[a[i]*a[j]%p]++;
d[i][a[i]*a[j]%p]+=2;
}
}
for(int x=0;x<=p-1;x++)
{
ll ans=0;
for(int k=1;k<=n;k++)
{
ll t=(x-a[k]+p)%p;
ans+=(c[t]-d[k][t]);
}
cout<<ans<<' ';
}
return 0;
}
K
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5 + 10, M = N * 2;
int h[N], ne[M], e[M], d[N] , n, m, a[N], b[N], now[N], q[N], idx;
void add(int a,int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int main()
{
int T;
cin >> n >> m >> T;
memset(h, -1, sizeof h);
for (int i = 1; i <= m; i++)
{
cin >> a[i] >> b[i];
d[a[i]]++, d[b[i]]++;
}
for (int i = 1; i <= m; i++)
{
if (d[a[i]] <= d[b[i]])
add(a[i], b[i]);
else
add(b[i], a[i]);
}
for (int j = 1; j <= T; j++)
{
int k;cin >> k;
for (int i = 1; i <= k; i++)
{
cin >> q[i];
now[q[i]] = j;
}
int res = 0;
for (int u = 1; u <= k; u++)
{
for (int i = h[q[u]]; i != -1; i=ne[i])
{
int jj = e[i];
if (now[jj] == j)res++;
}
}
cout << res << endl;
}
return 0;
}
F
很巧的思路(借鉴学习)(dfs+剪枝)
思路比较简单,我们不妨让起点有一个金币而终点没有(不影响结果),
假设我们现在在(x,y)这个点,且这个点没有怪兽,
如果我们能通过(x+1,y)或者(x,y+1)这两个点走到终点,
那么我们就可以将res++,同时我们将这个点标记为已经走过的点,
下次遇到这个点直接认定能否走到终点即可
#include<bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
#define endl '\n'
#define int long long
int n, k;
int a[N][5];
int dx[2] = { 0,1 };
int dy[2] = { 1,0 };
int res = 0;
bool dfs(int xx, int yy)
{
if (xx == n && yy == 3)return 1;
else
{
bool flag = 0;
for (int i = 0; i < 2; i++)
{
int tx = xx + dx[i], ty = yy + dy[i];
if (tx <= n && ty <= 3 && a[tx][ty] != -1)
{
if (a[tx][ty] == 0)
{
flag = 1;
continue;
}
if (dfs(tx, ty))//下一个点是否能走到终点
{
flag = 1;
}
}
}
if (flag == 0)a[xx][yy] = -1;//走不到终点,之后不走
else
{
res++;
a[xx][yy] = 0;
}
return flag;
}
}
void solve()
{
res = 0;
cin >> n >> k;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= 3; j++)
a[i][j] = 1;
while (k--)
{
int x, y;
cin >> x >> y;
a[x][y] = -1 * a[x][y];
}
dfs(1, 1);
cout << res << endl;
}
signed main()
{
int t;
cin >> t;
while (t--)
{
solve();
}
return 0;
}
E

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n;
ll f(ll x)
{
return n / x + x - 1;
}
int main()
{
int t;
ll L, R, sq, l, r, mid;
cin >> t;
while (t--)
{
cin >> n >> L >> R;
vector< pair<ll,ll> >res;
sq = sqrt(n + 0.5);
if (sq >= L && sq <= R)res.push_back({ f(sq),sq });
if (sq + 1 >= L && sq + 1 <= R)res.push_back({ f(sq + 1),sq + 1 });
res.push_back({ f(L),L });
res.push_back({ f(R),R });
sort(res.begin(), res.end());
l = L;
r = res[0].second;
while (l < r)
{
mid = (l + r) >> 1;
if (f(mid) <= res[0].first)r = mid;
else l = mid + 1;
}
printf("%lld\n", l);
}
return 0;
}
I
枚举
#include <bits/stdc++.h>
using namespace std;
#define mem(a,b) memset((a),(b),sizeof(a))
#define MP make_pair
#define pb push_back
#define fi first
#define se second
#define sz(x) (int)x.size()
#define all(x) x.begin(),x.end()
#define sqr(x) (x)*(x)
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> PII;
typedef pair<ll,ll> PLL;
typedef pair<int,ll> PIL;
typedef pair<ll,int> PLI;
typedef vector<int> VI;
typedef vector<ll> VL;
typedef vector<PII> VPII;
typedef vector<PLL> VPLL;
typedef vector<string> VS;
const int INF=0x3f3f3f3f;
const ll LLINF=0x3f3f3f3f3f3f3f3fLL;
const double PI=acos(-1.0);
const double eps=1e-6;
const int MAX=4e5+10;
const ll mod=998244353;
/********************************* std-head *********************************/
int n,a,b,c,d,v[6];
VL x;
ll gao(ll delta)
{
int i,pos,pre;
ll res,now,tmp;
res=-LLINF;
for(i=0;i<n;i++)
{
now=0;
pre=0;
tmp=x[i]-delta;
pos=upper_bound(all(x),tmp)-x.begin();
now+=1ll*(pos-pre)*v[1];
pre=pos;
tmp+=b-a;
pos=upper_bound(all(x),tmp)-x.begin();
now+=1ll*(pos-pre)*v[2];
pre=pos;
tmp+=c-b;
pos=upper_bound(all(x),tmp)-x.begin();
now+=1ll*(pos-pre)*v[3];
pre=pos;
tmp+=d-c+1;
pos=upper_bound(all(x),tmp)-x.begin();
now+=1ll*(pos-pre)*v[4];
pre=pos;
pos=n;
now+=1ll*(pos-pre)*v[5];
res=max(res,now);
}
return res;
}
int main()
{
int T,i;
ll ans;
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
x=VL(n);
for(auto &it:x) scanf("%lld",&it);
x.pb(LLINF);
sort(all(x));
scanf("%d%d%d%d",&a,&b,&c,&d);
for(i=1;i<=5;i++) scanf("%d",&v[i]);
ans=-LLINF;
VI tmp;
tmp.pb(a-1);
tmp.pb(a);
tmp.pb(b);
tmp.pb(c);
tmp.pb(d+1);
for(auto it:tmp) ans=max(ans,gao(it-(a-1)));
printf("%lld\n",ans);
}
return 0;
}

