BFS和DFS基础

搜索操作步骤：
1.找到所有可能的数据,并且用数据结构表示和存储。
2.优化。尽量多的排除不符合条件的数据，以减少搜索的空间。
3.用某个算法快速检索这些数据。

搜索的基本算法分为两种：BFS、DFS

BFS的代码实现 “BFS=队列”

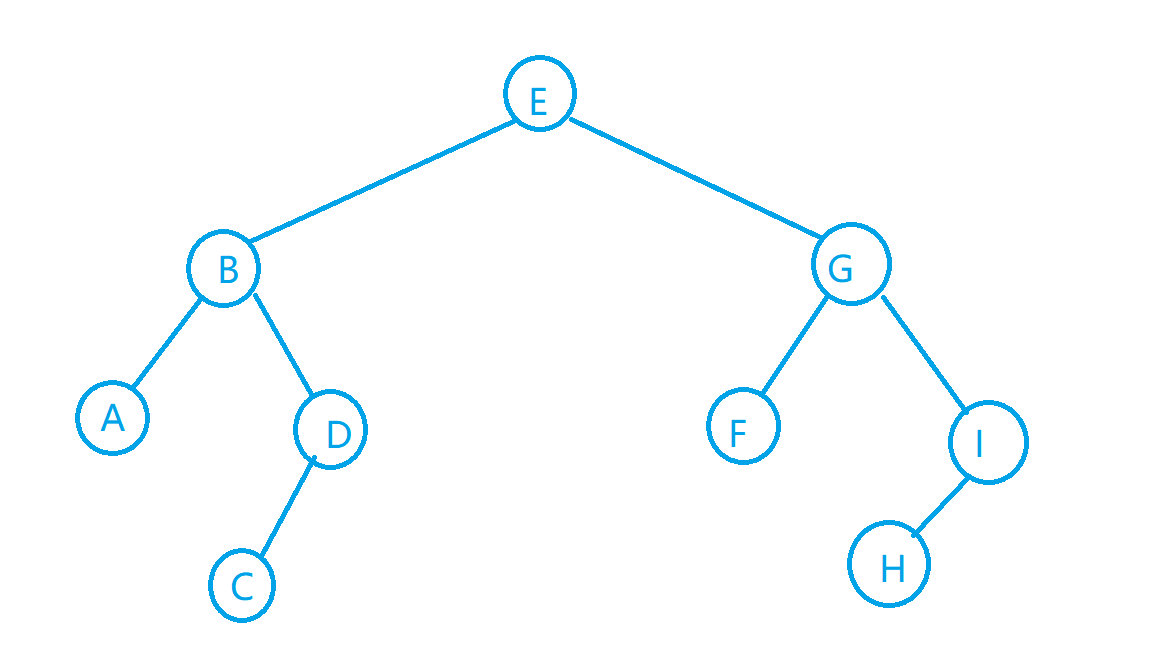
竞赛中一般使用静态版二叉树

from queue import Queue
class Node():
    def __init_(self):
        self.v=0
        self.l=0
        self.r=0
def newNode(v):#在树中创立新节点，并返回该节点的下标
    global idx
    tree[idx].v=v
    tree[idx].l=0
    tree[idx].r=0
    idx+=1
    return idx-1
def Insert(father,child,l_r):#插入孩子
    if l_r==0:
        tree[father].l=child
    else:
        tree[father].r=child
def buildtree():#建立一棵二叉树
    A=newNode('A');B=newNode('B');C=newNode('C')
    D=newNode('D');E=newNode('E');F=newNode('F')
    G=newNode('G');H=newNode('H');I=newNode('I')
    Insert(E,B,0);Insert(E,G,1);Insert(B,A,0);Insert(B,D,1)
    Insert(D,C,0);Insert(G,F,0);Insert(G,I,1);Insert(I,H,0)
    root=E
    return root

N=100005
tree=[Node() for i in range(N)]#从1开始记录每个节点的下标
idx=1

root=buildtree()
q=Queue()
q.put(root)
while q.qsize():
    tmp=q.get()
    print(tree[tmp].v,end=' ')
    if tree[tmp].l!=0:
        q.put(tree[tmp].l)
    if tree[tmp].r!=0:
        q.put(tree[tmp].r)

DFS的常见操作和代码框架 “DFS=递归”
1.DFS常见操作
竞赛中一般用静态版二叉树

class Node():
    def __init__(self):
        self.v=0
        self.l=0
        self.r=0

def newNode(v):
    global idx
    tree[idx].v=v
    tree[idx].l=0
    tree[idx].r=0
    idx+=1
    return idx-1

def Insert(father,child,l_r):
    if l_r==0:
        tree[father].l=child
    else:
        tree[father].r=child

def buildtree():
    A=newNode('A');B=newNode('B');C=newNode('C')
    D=newNode('D');E=newNode('E');F=newNode('F')
    G=newNode('G');H=newNode('H');I=newNode('I')
    Insert(E,B,0);Insert(E,G,1);Insert(B,A,0)
    Insert(B,D,1);Insert(D,C,0);Insert(G,F,0)
    Insert(G,I,1);Insert(I,H,0)
    root=E
    return root

def dfn_order(father):#时间戳
    global dfn_timer
    if father!=0:
        dfn_timer+=1
        dfn[father]=dfn_timer
        print('dfn[{}]={}'.format(tree[father].v,dfn[father]))
        dfn_order(tree[father].l)
        dfn_order(tree[father].r)

def visit_order(father):#DFS序
    global visit_timer
    if father!=0:
        visit_timer+=1
        print('visit[{}]={}'.format(tree[father].v,visit_timer))
        visit_order(tree[father].l)
        visit_order(tree[father].r)
        visit_timer+=1
        print('visit[{}]={}'.format(tree[father].v,visit_timer))

def deep_order(father):#树的深度
    global deep_timer
    if father!=0:
        deep_timer+=1
        deep[father]=deep_timer
        print('deep[{}]={}'.format(tree[father].v,deep[father]))
        deep_order(tree[father].l)
        deep_order(tree[father].r)
        deep_timer-=1

def num_node(father):#子树总结点数
    if father==0:
        return 0
    num[father]=num_node(tree[father].l)+num_node(tree[father].r)+1
    print('num[{}]={}'.format(tree[father].v,num[father]))
    return num[father]

def preorder(father):#先序遍历
    if father!=0:
        print(tree[father].v)
        preorder(tree[father].l)
        preorder(tree[father].r)

def inorder(father):#中序遍历
    if father!=0:
        inorder(tree[father].l)
        print(tree[father].v)
        inorder(tree[father].r)

def postorder(father):#后序遍历
    if father!=0:
        postorder(tree[father].l)
        postorder(tree[father].r)
        print(tree[father].v)

N=100005
tree=[Node() for i in range(N)]
idx=1

root=buildtree()

dfn=[0]*N
dfn_timer=0
print('dfn order:')
dfn_order(root)
print()

visit_timer=0
print('visit order:')
visit_order(root)
print()

deep=[0]*N
deep_timer=0
print('deep order:')
deep_order(root)
print()

num=[0]*N
print('num of tree:')
num_node(root)
print()

print('preorder:')
preorder(root)
print()

print('inorder:')
inorder(root)
print()

print('postorder:')
postorder(root)
print()

2.DFS代码框架

ans                                 #答案一般用全局变量表示
def dfs(层数，其他参数):            
    if 出局参数:                    #到达最底层或满足条件，出局
        更新答案
        return                      #返回上一层
    剪枝                            #进一步DFS之前剪枝
    for 枚举下一层可能的情况:       #对每种情况继续DFS
        if used[i]==0:              #如果状态i没有用过，就可以进入下一层
            used[i]=1               #标记状态i，表示已经用过，更底层不能再使用
            dfs(层数+1，其他参数)   #下一层
            used[i]=0               #恢复状态，回溯时不影响上一层对这个状态的使用
    return                          #返回更上一层

BFS和DFS的对比
时间复杂度差不多；BFS消耗空间更大；DFS可能搜索大量无效节点（可能超过最大递归深度）

#设置最大递归深度（默认1000）
import sys
sys.setrecursionlimit(10000000)

DFS适合找一个任意可行解；BFS适合找全局最优解
BFS技巧：去重。若该状态已经处理过，则不再入队。可用set去重。
DFS技巧：剪枝。
全球变暖
习题：
深度优先搜索
广度优先搜索
排列数字
n-皇后问题
单词接龙
Scales S