2020年复旦机试题目

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

2020年复旦机试题目

作者：

Pobz , 2023-01-17 17:36:12 , 所有人可见 , 阅读 1510

8

1

$\color{Orange}{题目1：排队打饭}$

题目标签

排序

题目描述

下课了，有 n 位同学陆续赶到⻝堂进⾏排队打饭，其中第 i 位同学的到达时间为 ai，
打饭耗时为 ti，等待时间上限为 bi，即如果其在第 ai+bi秒的时刻仍然没有轮到他开
始打饭，那么他将离开打饭队列，另寻吃饭的地⽅。问每位同学的开始打饭时间，或者
指出其提前离开了队伍（如果这样则输出 -1）。

输入描述

第⼀⾏⼀个整数 n (1<=n<=10^5)，表⽰来打饭的同学数量。
接下来 n ⾏，每⾏三个整数 a[i],t[i],b[i] (1<=a[i],t[i],b[i]<=10^9, 1<=i<=n)
分别表⽰每位同学的到达时间、打饭耗时、等待时间上限。 保证 a[1]<a[2]<…<a[n]

输入样例

输出样例

1 4 -1 6

类似题目
 原题链接
参考代码

#include <cstdio>

int main(){
    int n, arriveTime, dafanTime, waitTime, lastFinishTime=0;
    scanf("%d", &n);
    int result[n];
    for (int i=0; i<n; i++){
        scanf("%d%d%d", &arriveTime, &dafanTime, &waitTime);
        if (lastFinishTime > arriveTime + waitTime){  // 到了忍受上限，离开
            result[i] = -1;
        }else{
            result[i] = arriveTime > lastFinishTime ? arriveTime : lastFinishTime;
            lastFinishTime = result[i] + dafanTime;
        }
    }
    // 输出结果
    for (int i=0; i<n; i++){
        printf("%d", result[i]);
        if (i != n-1){
            printf(" ");
        }else{
            printf("\n");
        }
    }
    return 0;
}

$\color{Orange}{题目2：斗牛}$

网友评价

水题

给定五个 0~9 范围内的整数 a1, a2, a3, a4, a5。如果能从五个整数中选出三个并
且这三个整数的和为10 的倍数（包括 0），那么这五个整数的权值即为剩下两个没被
选出来的整数的和对 10 取余的结果，显然如果有多个三元组满⾜和是 10 的倍数，
剩下两个数之和对 10 取余的结果都是相同的；如果
选不出这样三个整数，则这五个整数的权值为 -1。
现在给定 T 组数据，每组数据包含五个 0~9 范围内的整数，分别求这 T 组数据中
五个整数的权值。

输入描述

第⼀⾏⼀个整数 T (1<=T<=1000)，表⽰数据组数。 接下来 T ⾏，
每⾏ 5 个 0~9 的整数，表⽰⼀组数据。

输出描述

第二行输入n个整数

输入样例：

输出样例：

2
-1
-1
0

提示

在第⼀组（1 0 0 1 0）中，三元组 0 0 0 的和为 0，是10的倍数，
剩余的1 1之和为2，对10取余为2。
在第⼆组中，不存在任何⼀个三元祖只和为10的倍数。
在第四组中，三元组 5 7 8 的和为 20，是10的倍数，剩余的 4 6 只和为 10，对 10取余为 0。
在第五组中，三元组 0 3 7 和三元组 0 4 6 的和都是10，是10 的倍数，但是根据简单的数论可知，如果存在多个三元组满⾜情况，那么剩余数字的结果之和对10 取余是相等的，在本例中和为10，对10取余为 0。

类似题目
 原题链接

#include<bits/stdc++.h>
using namespace std;

int main(){
    int n, i, j, k, a[5], mod;
    scanf("%d", &n);
    for(i=0; i<n; i++){
        bool exist = false;
        scanf("%d %d %d %d %d", &a[0], &a[1], &a[2], &a[3], &a[4]);
        mod = (a[0]+a[1]+a[2]+a[3]+a[4])%10;
        for(j=0; j<5; j++){
            if(exist) break;
            for(k=j+1; k<5; k++){
                if((a[j]+a[k])%10==mod){
                    printf("%d\n", mod);
                    exist = true;
                    break;
                }
            }
        }
        if(!exist) printf("-1\n");
    }
    return 0;
}

$\color{Orange}{题目3：打地鼠}$

题目标签

贪心

题目描述

给定 n 个整数 a1, a2, …, an 和⼀个 d，你需要选出若⼲个整数，
使得将这些整数从⼩到⼤排好序之后，任意两个相邻的数之差都不
⼩于给定的d，问最多能选多少个数出来。

输入描述

第⼀⾏两个整数 n,d (1<=n<=10^5,0<=d<=10^9)
分别表⽰整数个数和相邻整数差的下界。 
第⼆⾏ n个整数 a1, a2, …, an (1<=ai<=10^9, 1<=i<=n)
表⽰给定的 n 个整数。

输出描述

仅⼀⾏⼀个整数，表⽰答案。

输入样例：

6 2
1 4 2 8 5 7

输出样例：

提示

注意，选出的数在排序后，相邻两数之差不⼩于给定值。
⽐如，对于给定值 2，[1 4 7] 是⼀个满⾜条件的选择⽅案，但是[1 4 5] 却不是，
因为 5 - 4 = 1 < 2。
在本样例中，[1 4 7]，[1 4 8]，[1 5 7]，[1 5 8]，[2 4 7]，[2 4 8] 都是满⾜要求的选择⽅案，但是⽆论如何都没有办法得到⼀个选出 4 个
数且满⾜条件的⽅案，所以本样例的答案为 3。

类似题目
 原题链接

#include <cstdio>
#include <algorithm>

int main(){
    int n, d, ans=1;
    scanf("%d%d", &n, &d);
    int data[n];
    for (int i=0; i<n; i++){
        scanf("%d", &data[i]);
    }
    // 排序
    std::sort(data, data+n);  // 默认升序
    // Main Part
    int cmpBase = data[0];
    for (int i=1; i<n; i++){
        if (data[i] - cmpBase >= d){
            ans += 1;
            cmpBase = data[i];
        }
    }
    printf("%d\n", ans);
    return 0;
}

$\color{Orange}{题目4：序列}$

题目标签

动态规划

题目描述

给定⼀个⻓为 n 的序列 A，其中序列中的元素都是 0~9 之间的整数，对于⼀个⻓度同样为 n 整数序列B
，定义其权值为 |A_i-B_i| (1<=i<=n) 之和加上 (B_j-B_j+1)^2 (1<=j<n) 之和。求所有⻓为 n 的整数序列中，权值最⼩的序列的权值是多少。

输入描述

第⼀⾏⼀个整数 n (1<=n<=10^5)，表⽰序列 A 的⻓度。 第⼆⾏ n 个整数 a1, a2, …, an (0<=ai<=9, 1<=i<=n)，表⽰序列 A 中的元素。

输出描述

仅⼀⾏⼀个整数，表⽰答案。

输入样例：

6
1 4 2 8 5 7

输出样例：

提示

A 数组是 [1 4 2 8 5 7]
B 数组可以是 [3 4 4 5 5 6]。
权值为 |A_i - B_i| (1<=i<=n) 之和加上 (B_j - B_j+1)^2 (1<= j )

类似题目
 原题链接

#include <cstdio>
#include <algorithm>
#include <climits>

using namespace std;

int calculateAWeight(int a_value, int b_value){
    return abs(a_value - b_value);
}

int calculateBWeight(int b_value_i, int b_value_i2){
    return (b_value_i - b_value_i2) * (b_value_i - b_value_i2);
}

int main(){
    int n;
    scanf("%d", &n);
    int dataA[n], dp[n][10], ans = INT_MAX;
    //dp第一个表示b序列的第几个数，第二个表示该位是几
    for (int i=0; i<n; i++){
        scanf("%d", &dataA[i]);
    }
    // 初始化
    for (int i=0; i<=9; i++){
        dp[0][i] = calculateAWeight(dataA[0], i);
    }
    // DP Main
    for (int i=1; i<n; i++){
        for (int j=0; j<10; j++){
            int minWeight = INT_MAX;
            int weightA = calculateAWeight(dataA[i], j);
            for (int k=0; k<10; k++){
                int weightB = calculateBWeight(k, j);
                int total = dp[i-1][k] + weightB;
                if (total < minWeight){
                    minWeight = total;
                }
            }
            dp[i][j] = weightA + minWeight;
        }
    }
    for (int i=0; i<=9; i++){
        if (dp[n-1][i] < ans){
            ans = dp[n-1][i];
        }
    }
    printf("%d\n", ans);
    return 0;
}

$\color{Orange}{题目5：二叉搜索树}$

题目标签

二叉搜索树

题目描述

给定⼀个 1~n 的排列 P，即⻓度为 n，且 1~n 中所有数字都恰好出现⼀次的序列。现在按顺序将排列中的元素⼀⼀插⼊到初始为空的⼆叉搜索树中（左小右大），问最后每个节点的⽗亲节点的元素是什么。特别地，根节点的⽗亲节点元素视为 0。
输入样例的二叉树搜索树如下：

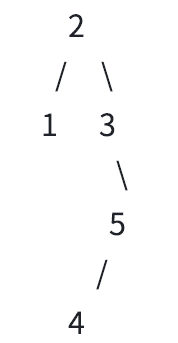
1 的⽗亲为 2，2 为根结点，所以⽗亲为 0，3 的⽗亲为 2，4 的⽗亲为 5，5 的⽗亲为 3。

输入描述

第⼀⾏⼀个整数 n (1<=n<=10^5)，表⽰排列 P 中的元素个数。
第⼆⾏ n 个整数 p1, p2, …, pn (1<=pi<=n, 1<=i<=n)，表⽰给定的排列。

输出描述

⼀⾏ n 个整数，其中第 i 个整数 ai 表⽰元素 i 对应节点的⽗亲节点的元素。特别地，根节点的⽗亲节 点元素视为 0。

输入样例：

5
2 3 5 1 4

输出样例：

2 0 2 5 3

类似题目
 原题链接

#include <cstdio>
#include <vector>

using namespace std;

typedef struct Node{
    int data;
    struct Node * left;
    struct Node * right;
    Node(int _data){
        data = _data;
        left = nullptr;
        right = nullptr;
    }
}*tree, Node;

vector<int> result;
tree root = nullptr;

void insert(tree &head, int target){
    if (head == nullptr){
        head = new Node(target);
    }else{
        if (target < head->data){
            insert(head->left, target);
        }else{
            insert(head->right, target);
        }
    }
}

void inorderTraverse(tree head, int parentData){
    if (head != nullptr){
        inorderTraverse(head->left, head->data);
        result.push_back(parentData);
        inorderTraverse(head->right, head->data);
    }
}

int main(){
    int n, tmp;
    scanf("%d", &n);
    for (int i=0; i<n; i++){
        scanf("%d", &tmp);
        insert(root, tmp);
    }
    inorderTraverse(root, 0);
    for (int i=0; i<result.size(); i++){
        printf("%d", result[i]);
        if (i != result.size() - 1){
            printf(" ");
        }else{
            printf("\n");
        }
    }
    return 0;
}

6 评论

Pobz 2023-03-15 20:00

斗牛
其实就是判断是否有三数之和为10的倍数，而且确定总共只有五个数，那么可以用fou循环来解决，但是为了代码美观而且看起来牛掰点，还是使用了回溯法，二者的时间复杂度和空间复杂度是相同的。最后如果三数之和为10的倍数，那么只要五数之和减去三数之和就可以了。时间复杂度：O(n) 空间复杂度：O(1)

Pobz 2023-03-15 20:00

回溯法：使用visited数组来记录每个元素的是否被访问过，每次确定一个元素，然后递归确定其他元素

Pobz 2023-03-15 20:01 回复了 Pobz 的评论

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

//回溯法得到其中三数之和，若没有10的倍数，返回-1
int judge(int sum,vector<int>& visited,vector<int>D,int num) {
    if (num > 3)    return -1;
    if (num == 3 && sum % 10 == 0)  return sum;
    for (int i = 0; i < D.size(); i++) {
        if (visited[i] == 0) {
            visited[i] = 1;
            int f = judge(sum + D[i], visited, D, num + 1);
            if (f != -1)    return f;
            visited[i] = 0;
        }
    }
    return -1;
}

int main()
{
    int T;
    cin >> T;
    int N = 5;
    vector<vector<int>>data(T, vector<int>(N));
    for (int i = 0; i < T; i++) {
        for (int j = 0; j < N; j++) {
            cin >> data[i][j];
        }
    }
    vector<int>result;
    vector<int> visited(N, 0);  //记录已被访问过的数
    for (int i = 0; i < T; i++) {
        int sum = 0, num = 0;
        fill(visited.begin(), visited.end(), 0);
        int flag = judge(sum, visited, data[i], num);
        if (flag != -1) {   //存在三数之和为10的倍数
            int S = 0;
            for (int j = 0; j < N; j++) S += data[i][j];
            result.push_back((S - flag) % 10);  //总和减去三数之和就是剩余两数之和
        }
        else  result.push_back(flag);
    }
    for (int i = 0; i < result.size(); i++) cout << result[i] << endl;
}