bfs与dfs
主要是复习课
视频在这里
声音有点沉重抱歉hh
时间有点长抱歉hh
debug有点慢抱歉hh
(抱歉hh三联)
例题一:跳台阶
一个楼梯共有n级台阶,每次可以走一级或者两级,问从第0级台阶走到第n级台阶一共有多少种方案。
输入格式
共一行,包含一个整数n。
输出格式
共一行,包含一个整数,表示方案数。
数据范围
1≤n≤15
输入样例:
5
输出样例:
8
这道题的话是dfs。
每次可以向上走一级台阶或者两级台阶。
所以n = 5搜索树如下:
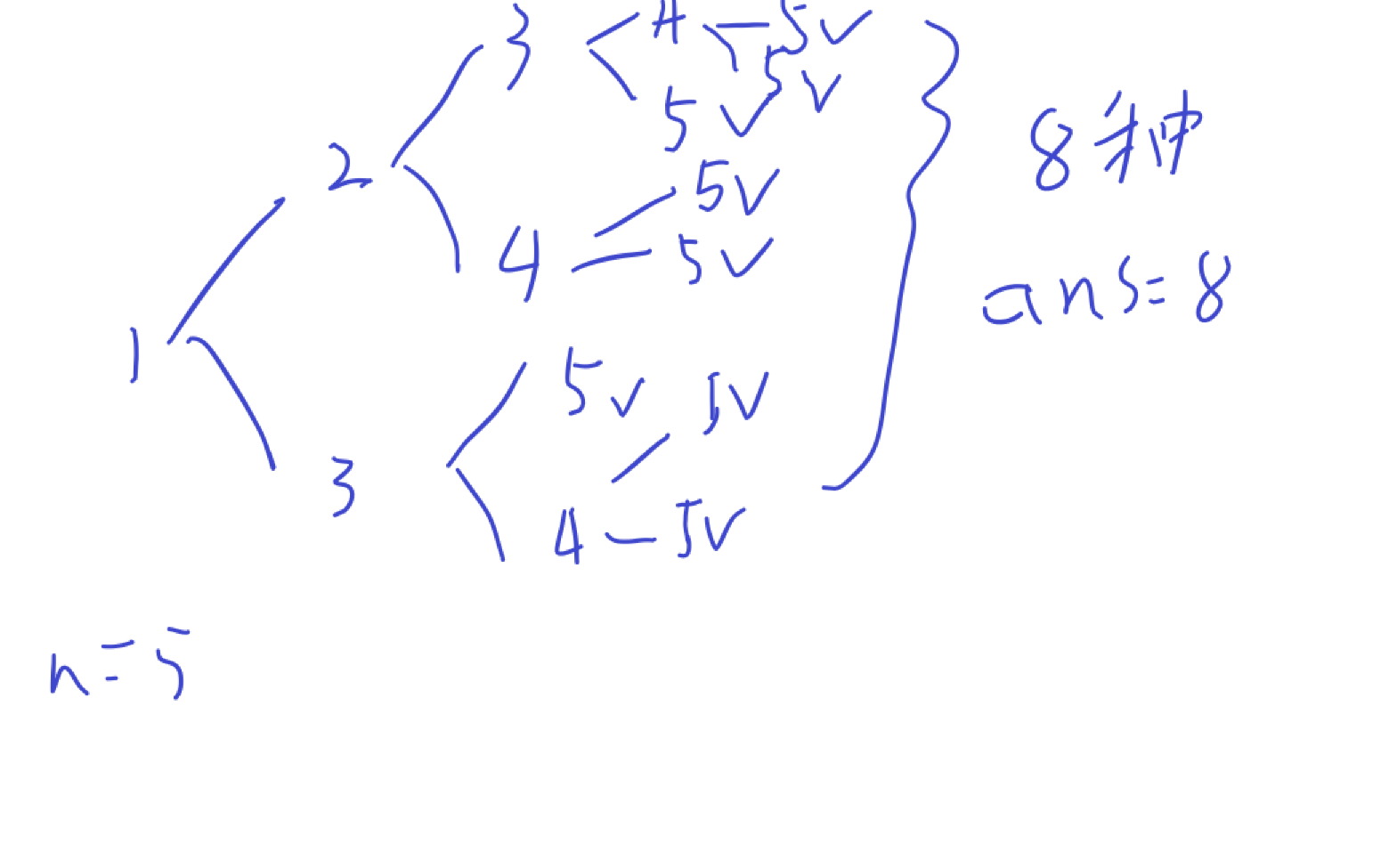
注意每次搜索时要判断是否越界。
然后就是代码了。
#include<iostream>
using namespace std;
int ans = 0;
int n;
void dfs(int u)
{
if(u >= n)
{
ans ++;
return;
}
dfs(u + 1);//跳一级台阶
dfs(u + 2);//跳两级台阶
}
int main()
{
scanf("%d", &n);
dfs(1);
printf("%d\n", ans);
return 0;
}
例题2:走方格
给定一个n*m的方格阵,沿着方格的边线走,从左上角(0,0)开始,每次只能往右或者往下走一个单位距离,问走到右下角(n,m)一共有多少种不同的走法。
输入格式
共一行,包含两个整数n和m。
输出格式
共一行,包含一个整数,表示走法数量。
数据范围
1≤n,m≤10
输入样例:
2 3
输出样例:
10
这道题我们还是用dfs来做。
每次可以向右或向下走。
接下来我们来看一下n = 2, m = 2的搜索树。
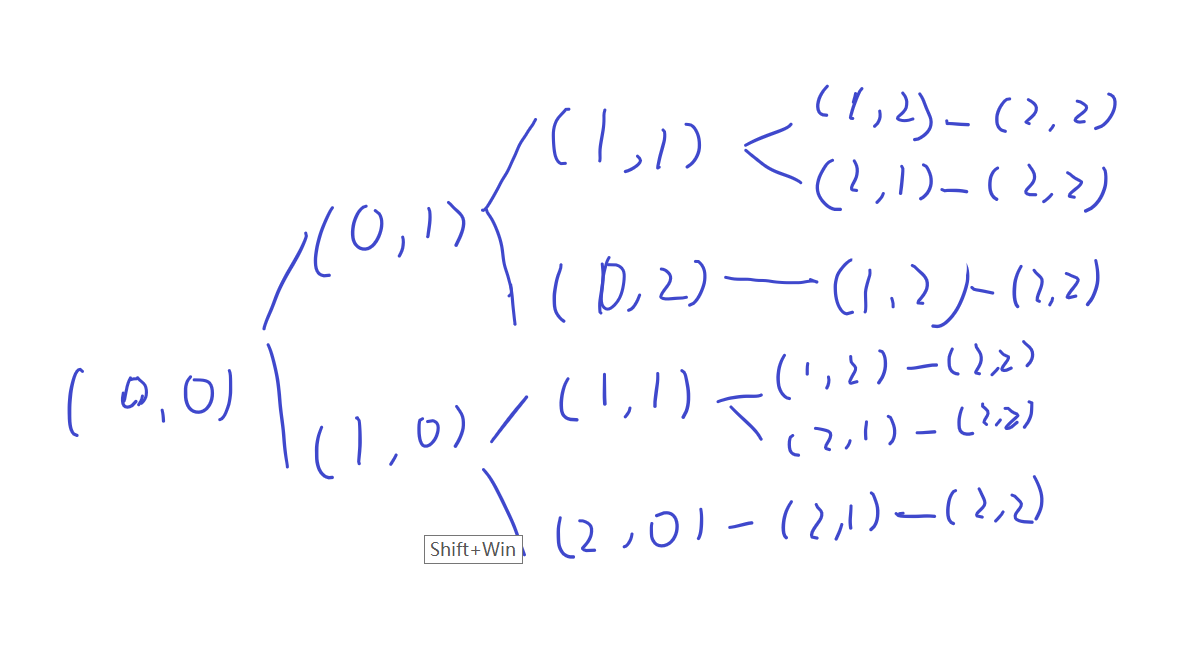
接下来我们考虑一下dfs函数的写法。
首先,我个人认为dfs依据的是递推递归的思想。
这个函数里我们可以写两项。
dfs(x, y);
x表示当前搜的点的x坐标,y表示当前搜到点的y坐标。
每次如果已经越界直接return。
走到右下角先ans++再return。
否则就继续搜。
dfs部分代码:
void dfs(int x, int y)
{
if(x > n || y > m) return;
if(x == n && y == m)
{
ans ++;
return;
}
dfs(x + 1, y);
dfs(x, y + 1);
}
完整代码:
#include<iostream>
using namespace std;
int n, m;
int ans = 0;
void dfs(int x, int y)
{
if(x > n || y > m) return;
if(x == n && y == m)
{
ans ++;
return;
}
dfs(x + 1, y);
dfs(x, y + 1);
}
int main()
{
scanf("%d%d", &n, &m);
dfs(0, 0);
printf("%d\n", ans);
return 0;
}
例题3:排列
给定一个整数n,将数字1~n排成一排,将会有很多种排列方法。
现在,请你按照字典序将所有的排列方法输出。
输入格式
共一行,包含一个整数n。
输出格式
按字典序输出所有排列方案,每个方案占一行。
数据范围
1≤n≤9
输入样例:
3
输出样例:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
这道题的具体讲解在这里
以前讲过了这里就直接上代码了。
#include<bits/stdc++.h>
using namespace std;
const int N = 10;
int n;
int path[N];
bool st[N];
void dfs(int u)
{
if(u == n)
{
for(int i = 0; i < n; i ++) cout << path[i] << ' ';
cout << endl;
return;
}
for(int i = 1; i <= n; i ++)
{
if(!st[i])
{
st[i] = true;
path[u] = i;
dfs(u + 1);
path[u] = 0;
st[i] = false;
}
}
}
int main()
{
scanf("%d", &n);
dfs(0);
return 0;
}
例题4:蛇形矩阵
输入两个整数n和m,输出一个n行m列的矩阵,将数字 1 到 n*m 按照回字蛇形填充至矩阵中。
具体矩阵形式可参考样例。
输入格式
输入共一行,包含两个整数n和m。
输出格式
输出满足要求的矩阵。
矩阵占n行,每行包含m个空格隔开的整数。
数据范围
1≤n,m≤100
输入样例:
3 3
输出样例:
1 2 3
8 9 4
7 6 5
这道题是一个bfs。
主要存4个变量:
x:x坐标
y:y坐标
d:方向。
0:右
1:下
2:左
3:上
k:要填的数。
首先从
x = 0, y = 0
开始填。
k从一开始。
k的范围是n * m,k每次++。
这样循环就出来了。
for(x = 0, y = 0, k = 1; k <= n * m; k ++)
注意为了方便我们把4联通搞成偏移量。
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};
然后每次d更新的条件是越界或者已经被搜过。
if(px < 0 || px >= n || py < 0 || py >= m || st[px][py])
更新做两件事:
1. 更新d
2. 更新px和py、
if(px < 0 || px >= n || py < 0 || py >= m || st[px][py])
{
d = (d + 1) % 4;
px = x + dx[d], py = y + dy[d];
}
然后把这个点填上。
res[px][py] = k;
再把这个点标记一下。
st[px][py] = true;
完整代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 110;
int n, m;
int a[N][N];
bool st[N][N];
int main()
{
scanf("%d%d", &n, &m);
int x = 0, y = 0, d = 0, k = 1;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1,0 ,-1};
for(x = 0, y = 0; k <= n * m; k ++)
{
int px = x + dx[d], py = y + dy[d];
if(px < 0 || px >= n || py < 0 || py >= m || st[px][py])
{
d = (d + 1) % 4;
px = x + dx[d], py = y + dy[d];
}
a[x][y] = k;
st[x][y] = true;
x = px, y = py;
}
for(int i = 0; i < n; i ++, cout << endl)
for(int j = 0; j < m; j ++)
cout << a[i][j] << ' ';
return 0;
}
例题5:扫雷游戏
这道题ACWINIG没有就把luogu的链接粘上了。
其实这道题是我前几天做蓝桥杯青少组模拟赛的时候遇到的。
后来去各种OJ上搜了一下找到了。
此题务必开c++11编译!!!!
题目描述
扫雷游戏是一款十分经典的单机小游戏。在nn行mm列的雷区中有一些格子含有地雷(称之为地雷格),其他格子不含地雷(称之为非地雷格)。玩家翻开一个非地雷格时,该格将会出现一个数字——提示周围格子中有多少个是地雷格。游戏的目标是在不翻出任何地雷格的条件下,找出所有的非地雷格。
现在给出nn行mm列的雷区中的地雷分布,要求计算出每个非地雷格周围的地雷格数。
注:一个格子的周围格子包括其上、下、左、右、左上、右上、左下、右下八个方向上与之直接相邻的格子。
输入格式
第一行是用一个空格隔开的两个整数nn和mm,分别表示雷区的行数和列数。
接下来nn行,每行mm个字符,描述了雷区中的地雷分布情况。字符’*’表示相应格子是地雷格,字符’?’表示相应格子是非地雷格。相邻字符之间无分隔符。
输出格式
输出文件包含nn行,每行mm个字符,描述整个雷区。用’*’表示地雷格,用周围的地雷个数表示非地雷格。相邻字符之间无分隔符。
输入输出样例
输入 #1
3 3
*??
???
?*?
输出 #1
*10
221
1*1
输入 #2
2 3
?*?
*??
输出 #2
2*1
*21
说明/提示
对于 100\%100%的数据, 1≤n≤100, 1≤m≤1001≤n≤100,1≤m≤100。
这道题就是进行一步宽搜。
然后这道题稍微讲一下8联通的处理方式。
一般8联通我们选择使用3*3循环然后把中间扣掉。
pair<int, int> t = {x, y};
for(int i = t.first - 1; i <= t.first + 1; i ++)
for(int j = t.second - 1; j <= t.second + 1; j ++)
{
if(i == t.first && j == t.second) continue;
//blahblahblah
}
然后再来说一下这题的存储。
本题无需开st数组。
用g数组存储输入。
用d数组来表示具体的值。
memset(d, 0, sizeof d);
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
{
cin >> g[i][j];
if(g[i][j] == '*') d[i][j] = -1;
}
这里其实memset不开也能过啦。
每次如果这个点有雷就把d数组对应的位置搞成-1。
然后宽搜的话就是看看这个点是不是雷
是的话就进行8联通拓展。
这一步比较关键。
首先遍历所有点然后开一个pair。
开pair是个人习惯啦
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
{
pair<int, int> t = {i, j};
}
接着我们8联通。
for(int x = t.first - 1; x <= t.first + 1; x ++)
for(int y = t.second - 1; y <= t.second + 1; y ++)
{
}
如果越界,continue。
if(x < 0 || x >= n || y < 0 || y >= n) continue;
如果是中间,continue。
if(x == t.first && y == t.second) continue;
如果原来判断的点不是雷,说明不能更新,continue…………
if(d[i][j] != -1) continue;
如果当前要更新的点是雷,继续continue……
if(d[x][y] == -1) continue;
好不容易,更新一下……
d[x][y] += 1;
这一部分完整代码:
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
{
pair<int, int> t = {i, j};
for(int x = t.first - 1; x <= t.first + 1; x ++)
for(int y = t.second - 1; y <= t.second + 1; y ++)
{
if(x < 0 || x >= n || y < 0 || y >= n) continue;
if(x == t.first && y == t.second) continue;
if(d[i][j] != -1) continue;
if(d[x][y] == -1) continue;
d[x][y] += 1;
}
}
最后输出。
for(int i = 0; i < n; i ++, cout << endl)
for(int j = 0; j < m; j ++)
{
if(d[i][j] == -1) printf("*");
else cout << d[i][j];
}
完整代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 110;
int n, m;
char g[N][N];
int d[N][N];//有雷:-1
int main()
{
scanf("%d%d", &n, &m);
memset(d, 0, sizeof d);
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
{
cin >> g[i][j];
if(g[i][j] == '*') d[i][j] = -1;
}
for(int i = 0; i < n; i ++)
for(int j = 0; j < m; j ++)
{
pair<int, int> t = {i, j};
for(int x = t.first - 1; x <= t.first + 1; x ++)
for(int y = t.second - 1; y <= t.second + 1; y ++)
{
if(x < 0 || x >= n || y < 0 || y >= n) continue;
if(x == t.first && y == t.second) continue;
if(d[i][j] != -1) continue;
if(d[x][y] == -1) continue;
d[x][y] += 1;
}
}
for(int i = 0; i < n; i ++, cout << endl)
for(int j = 0; j < m; j ++)
{
if(d[i][j] == -1) printf("*");
else cout << d[i][j];
}
return 0;
}


赞!写的很好!
有 2么
orz
orz