KMP：

定义：Knuth-Morris-Pratt字符串查找算法，简称为“KMP算法”，常用于在一个文本串S内查找一个模式串P的出现位置，这个算法由Donald Knuth、Vaughan Pratt、James H. Morris三人于1977年联合发表，故取这3人的姓氏命名此算法。

注：以下字符串起始下标均为1

引入概念：

• 前缀：指的是字符串的子串中从原串最前面开始的子串
  如abcdef的前缀有：a,ab,abc,abcd,abcde

• 后缀：指的是字符串的子串中在原串结尾处结尾的子串
  如abcdef的后缀有：f,ef,def,cdef,bcdef

• Next[i]：满足 以1开始的前缀 和 以i结尾的后缀 相等条件的最大长度（长度<i）

Next数组求解：
求解Next数组，只涉及模式串P，要将模式串作为文本串（即S=P）

• 边界：Next[1]=0;（由定义即可得到）

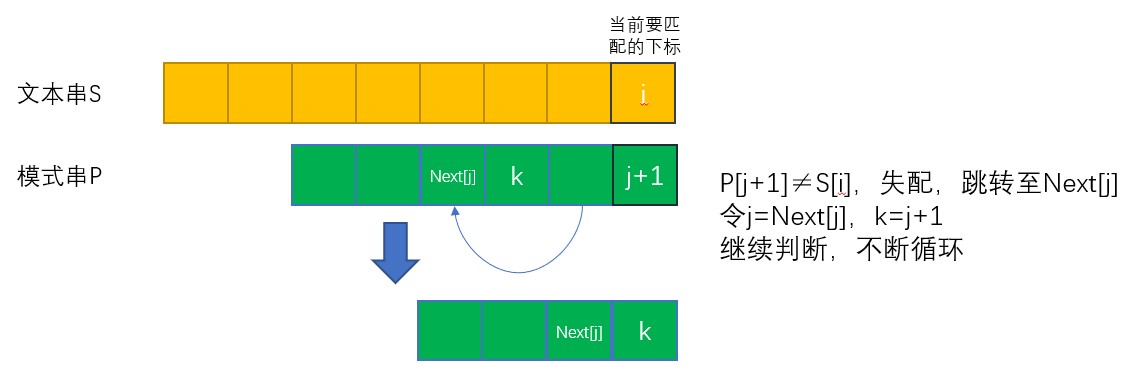
• 匹配状态：j + 1表示当前P要匹配的下标，i表示当前S串要匹配的下标
  若P[j+1]=S[i]，直接匹配成功，则Next[j]=Next[j-1]+1;
  若P[j+1]≠S[i]，匹配失败，需要根据Next[j]不断向前跳j，直到匹配成功或者j=0；

void get_Next(char S[], char P[])//S:文本串 P:模式串(此时S = P)
{
    int n = strlen(S + 1);
    int m = strlen(P + 1);

    Next[1] = 0;
    for (int i = 2, j = 0; i <= n; i++)
    {
        while (j && S[i] != P[j + 1]) j = Next[j];
        if (S[i] == P[j + 1]) j++;
        Next[i] = j;
    }
}

Next数组运用：
过程和求解基本一致，直接用原文本串即可。

//例：获取文本串S 中 模式串P 的个数
int get_count(char S[], char P[])
{
    int n = strlen(S + 1);
    int m = strlen(P + 1);

    int cnt = 0; //统计个数

    for (int i = 1, j = 0; i <= n; i++)
    {
        while (j && S[i] != P[j + 1]) j = Next[j];
        if (S[i] == P[j + 1]) j++;
        if (j == m) //找到匹配成功项
            cnt++, j = Next[j];
    }

    return cnt;
}

时间复杂度： O(N + M)

相关性质（周期性）：

• 若模式串P中 j / (j - Next[j]) == 0, 则P中必存在最小循环节(P[1~j-Next[j]),且循环次数为 j / (j - Next[j])。
  证明方法可通过切割移项法证“循环节”成立，通过反证法证“最小”成立
• 若模式串P中 j / (j - Next[j]) ≠ 0, 则P中必存在最小循环节(P[1~j-Next[j]),且循环次数为 j / (j - Next[j])，余项为P[1 ~ j % Next[j]]。
  证明方法如上

不知道理解得对不对，请大佬指教