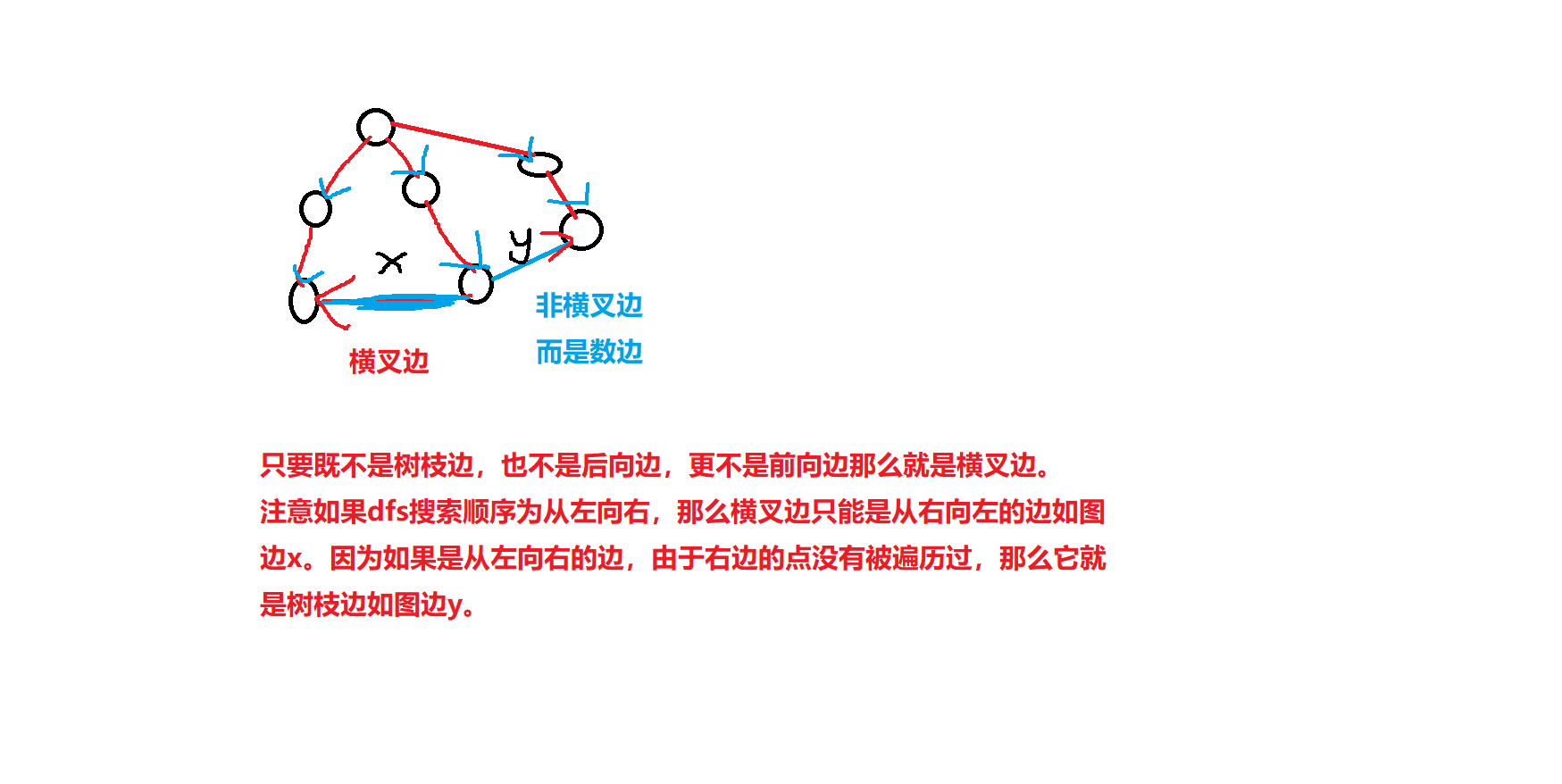
什么是横叉边？

dfs生成树与强联通分量的关系。
如果节点u是某个强联通分量在搜索树中遇到的第一个节点，那么这个强联通分量的其余节点肯定是在搜索树中以u为根的子树。u被称为这个强联通分量的根。
反证法：假设有个节点v在该强连通分量中但是不在以u为根的子树中，那么u到v的路径肯定有一条离开子树的边，但是这样的边只可能是横叉边或者后向边，然而这两条边都要求指向的节点已经被访问过了，这就和u是第一个被访问的节点矛盾了。得证。
如何求解有向图中的强联通分量？
如果按照定义出发，用双向遍历取交集的方法求解的话，之间复杂的为O(N^2 +M)。更好的方法有Kosaraju算法或者Tarjon算法，两者的复杂度都是O(N + M)但是Kosaraju需要做两遍DFS，而Tarjon算法只要做一遍效果更优。
Tarjon 算法
基于对图的深度优先遍历搜索算法，每一个强联通分量为搜索一颗搜索子树。搜索时，把当前搜索树中未处理的节点假如堆栈，回溯是可以砍断栈顶元素中的节点是否为一个强联通分量。
定义DFN(u)为节点u搜索的次序编号(时间戳)，Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。
tarjon算法模板

void tarjon(int u)
{
    dfn[u] = low[u] = ++ timestamp; // 每次把low 赋值为当前的时间戳
    stk[++ top] = u, in_stk[u] = ture;// 第一艹遍历到的节点要放到栈中 并且标记当前点已经在栈中。
    for(int i = h[u); ~i; i = ne[i])
    {
        int j = e[i];
        if(!dfn[j])//如果子节点没有遍历过得话就进去
        {
            tajon(j);
            low[u] = min(low[u], low[j]);//回溯用子节点更新父节点
        }
        else if(in_stk[j]) low[u] = min(low[u], dfn[j]);// 如果已经遍历过了但是仍然在栈中就用这个点的时间戳比较是否可以更新low[u]
    }

    if(low[u] == dfn[u])//回溯的时候只有当它的时间戳与它的low函数值相等表示这个点是一个强联通分量的根，并且从栈顶到这个 点之间的所以数都是强联通分量的点
    {
        ++ssc_cnt;//一个强联通分量的标号
        do
        {
            int y = stk[top --];// 出栈
            in_stk[y] = false; // 标记不在栈中
            id[y] = ssc_cnt;//标记该点所在的强联通标号
        }while(y != u);//结束条件直到该点出栈
    }
}

算法正确性分析： 不会。
一位大佬的模拟与分析