什么是哈希表

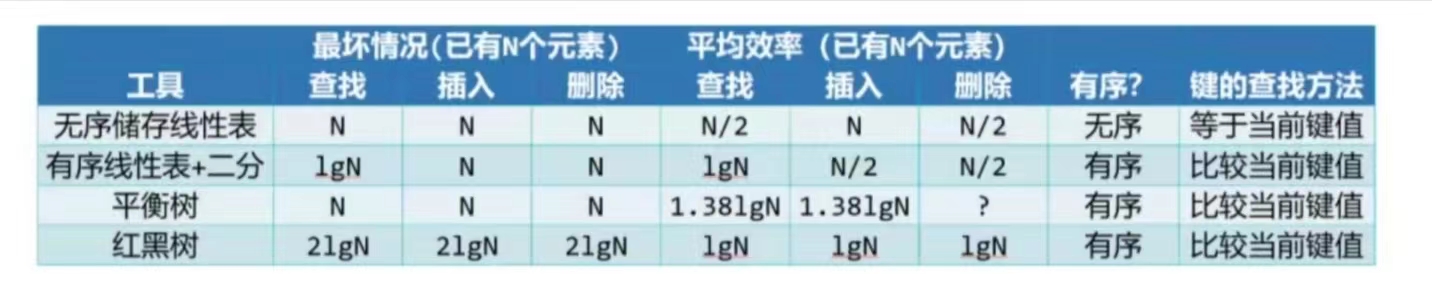
讲哈希之前，我们先分析一下已经学过的几种数据结构的效率

所谓 “键-值”，可以简单理解为查字典时，那个字就是“键”，解释就是“值”。也就是说，我们是通过键，查找到值。

我们已经学过的键值查询方法有：

无序的数组存放、有序的数组配合二分查找键、平衡树、红黑树（map、set)

哈希 = Hash = 散列表杂凑函数；哈什

哈希表是一种以 键-值(key-indexed) 存储数据的结构，我们只要输入待查找的值即 key，即可查找到其对应的值。并且在时间空间博弈中，逼近于常数级别时间复杂度。

哈希的思路很简单！
如果是整数，那么使用一个简单的无序数组，键为索引，值为其对应的值。
如果键不是整数（比如字符串）怎么办？使用某个方法，转换为整数即可！

常用哈希函数

将键映射成索引（数组下标），这种映射函数就是哈希函数

整数

对于范围为 $1 \sim 2 \times 10^9$ 的整数，显然不能直接开一个这么大的数组
我们一般的处理方法为简单取除以某个数的余数，即：$x \to x \% M$
这样就只需要开一个大小为 $M$ 的数组即可！$M$ 一般选择不常见的质数或者你的幸运数字，比如说生日

int hash(int x) {
    return x%M;
}

字符串

目前比较高效、冲突较少的方法是将其作为一个大整数来对 $M$ 取余处理，然后进制一般采用 $31$，怕被卡也可以换成 $29$ 等质数，玄学避免冲突
如果每一位都换觉得太耗时，也可以每隔 $k$ 个作为一位

int hash(string s) {
    int res = 0;
    // 每隔 3 个的话，就可以把 ++i 换成 i += 3
    for (int i = 0; i < s.size(); ++i) {
        res = (s[i] + res*31%M) % M;
    }
    return res;
}

解决冲突的方法

哈希的核心就是压缩空间后尽可能减少冲突，这是时间与空间的博弈
哈希出现冲突不可避免
我们解决冲突问题，一般常用两种方法：拉链法、线性探测法

拉链法：

假如 $A$ 和 $B$ 都 hash 到了 $C$，那么我们开一个链表来存储所有 hash 到 $C$ 的元素

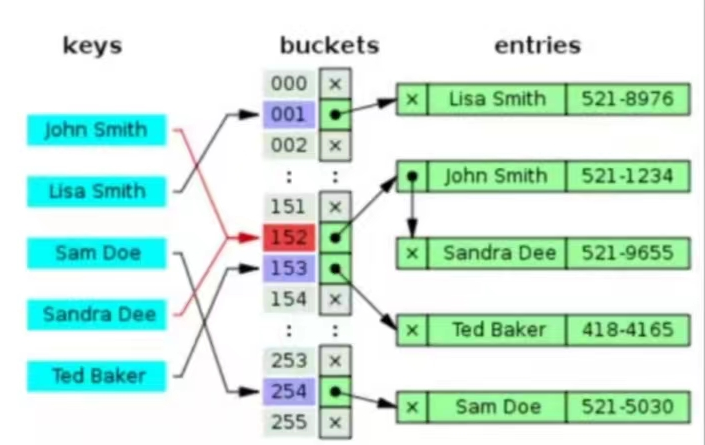
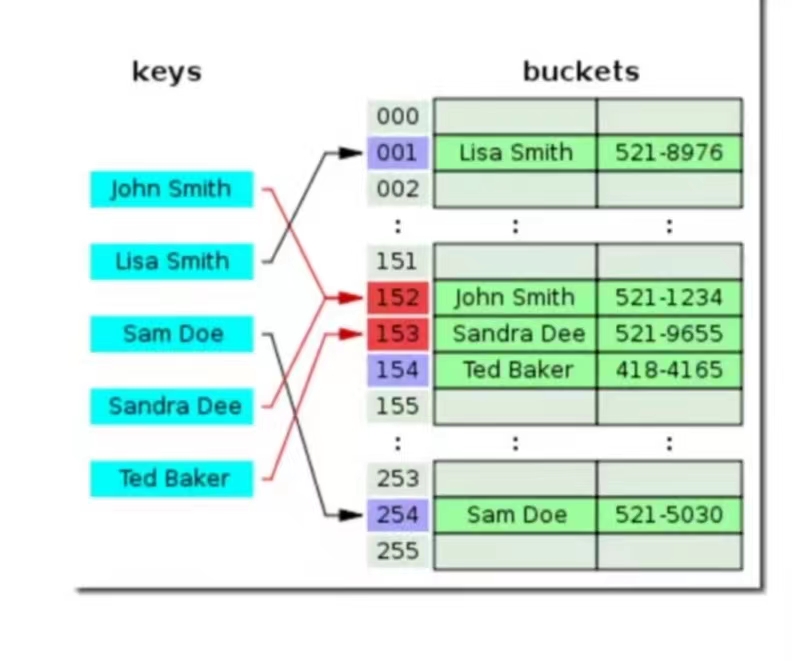
线性探测法：

当碰撞发生时，直接检查散列表中的下一个位置即将索引值加 $1$，这样的线性探测会出现三种结果：

1. 命中，该位置的键和被查找的键相同
2. 未命中，键为空
3. 该位置和被查找的键不同，继续查找

这样的缺点也很明显，插入时存在冲突的话，查找时可能更劣

例题：图书管理

// 使用线性探测法解决哈希冲突
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::string;

const int M = 1008611; 

string a[M];

int hash(string s) {
    int res = 0;
    for (int i = 0; i < s.size(); ++i) {
        res = (s[i] + res*31%M) % M;
    }
    return res;
}

int main() {
    int n;
    cin >> n;

    rep(i, n) {
        string type, book;
        cin >> type;
        getline(cin, book);
        int key = hash(book);
        if (type == "add") {
            while (a[key] != "" and a[key] != book and key+1 < M) key++;
            a[key] = book;
        }
        else {
            while (a[key] != "" and a[key] != book and key+1 < M) key++;
            if (a[key] == book) puts("yes");
            else puts("no");
        }
    }

    return 0;
}

字符串哈希

关于字符串哈希：把字符串有效地转化为一个整数

在计算机里，用的是二进制编码。在很多语言里，都是用数字作为数组的下标。因为用数字来存储、表达一个数据非常方便

如果能有一种算法，把每个字符串有效地、“唯一” 地映射到每个“不同”的整数，我们就能很好的处理字符串问题

一个 hash 函数，使得每一个字符串都能够映射到一个整数上
比如 hash[i] = (hash[i-1]*p + idx(s[i])) % mod
字符串：$abc$，$bbc$，$aba$，$aadaabac$
字符串下标从 $0$ 开始
先把 $a$ 映射为 $1$，$b$ 映射为 $2$，$c \to 3$，$d \to 4$，即 $idx(a) = 1$，$idx(b) = 2$，$idx(c) = 3$，$idx(d) = 4$
尝试对字符串进行 hash

具体举个例子：
假设取 $p = 13$，$mod = 101$
先把 $abc$ 映射为一个整数
hash[0] = 1，表示 $a$ 映射为 $1$
hash[1] = (hash[0]*p+idx(b))%mod = 15，表示 $ab$ 映射为 $15$
hash[2] = (hash[1]*p+idx(c))%mod = 97
$abc$ 映射为 $97$

子串哈希

快速求解出子串的 hash 值

$\operatorname{hash}[1] = s1$
$\operatorname{hash}[2] = s1\*p + s2$
$\operatorname{hash}[3] = s1\*p^2 + s2\*p + s3$
$\operatorname{hash}[4] = s1\*p^3 + s2\*p^2 + s3\*p + s4$
$\operatorname{hash}[5] = s1\*p^4 + s2\*p^3 + s3\*p^2 + s4\*p + s5$

如果我们求 $s3s4$ 形成的 hash 值，应该是 $s3\*p + s4$
$s3\*p + s4 = \operatorname{hash}[4] - \operatorname{hash}[2]\*p^{4-3+1} = \operatorname{hash}[4] - \operatorname{hash}[2] \* p^2$

一个子串 $j \sim i$ 的 $\operatorname{hash}$ 值我们可以如下表示：

$$\operatorname{hash}[i] - \operatorname{hash}[j-1] \* p^{i-j+1}$$

为了防止相减变成负数，更加通项的表示为：

$$\operatorname{hash} = \bigg((\operatorname{hash}[i] - \operatorname{hash}[j-1]\*p^{i-j+1})\% \bmod + \bmod\bigg) \% \bmod$$

例题：子串查找

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using namespace std;
using ll = long long;

const int p = 31;
const int mod = 1000000007;

ll h[1000005];

int main() {
    string a, b;
    cin >> a >> b;

    ll hb = 0;
    int n1 = a.size(), n2 = b.size();
    // 计算 b 字符串的 hash 值
    rep(i, n2) {
        hb = (b[i] + hb*p%mod)%mod;
    }

    int cnt = 0;
    // 计算 a 字符串的 hash[i]
    ll pb = 1;
    for (int i = 1; i <= n2; ++i) pb = pb*p%mod;
    for (int i = 1; i <= n1; ++i) {
        h[i] = (h[i-1]*p%mod + a[i-1])%mod;
        if (i >= n2) {
            ll sub = ((h[i]-h[i-n2]*pb)%mod + mod)%mod;
            if (sub == hb) cnt++;
        }
    }

    cout << cnt << '\n';

    return 0;
}