Awcing算法基础课模板
[TOC]
快速排序
// yxc大佬的模板,我不太理解,我觉得它没有体现一个while循环后,q[j]左边的数大于q[j],右边的小于q[j] , 但就像魔法一样,能把排序排出来 , 还不容易错(没有> 、 >=的边界问题)
//粗想下来,思想大致也是:将左右两边分别小于pivot和大于pivot的数交换 , 从而实现左右分离
//--2022.12.17 18:57
//上面的疑惑解决了!yxc大佬这个模板也是实现了:以pivot为界,左边大于pivot,右边小于pivot,可以举实例来看看 --2022.12.17.23:46 而且非常简洁!
#include<iostream>
using namespace std;
const int N=1e6 + 10;//数组最大长度
int n;//输入数字个数
int q[N];
void quick_sort(int q[] , int l ,int r)
{
if(l >= r) return;//可以换成(l == r),一样的,不会出现l > r的情况,除非输入数据有误(写l>=r也是这个目的)
int i = l - 1, j = r + 1;//指针向两端去一格,因为后面用do - while
int x = q[(l + r) >> 1];//可换成x=q[l] ,但取中间q[l + r >> 1]在一般的数据测试集中总花费时间少,具体分析可见《算法笔记 胡凡》快排部分
while(i<j)
{
do ++i ; while(q[i] > x);
do --j ; while(q[j] < x);
if(i<j) swap(q[i] , q[j]);
}
//一个while循环下来,q[j]左边的数>=q[j] , 右边的数 <= q[j] ,成了分界点
quick_sort(q , l , j);
quick_sort(q , j+1 , r);
}
int main()
{
scanf("%d",&n);
for(int i=0;i<n;i++) scanf("%d",&q[i]);
quick_sort(q,0,n-1);
for(int i=0; i<n ; i++) printf("%d ",q[i]);
return 0;
}
一般的快排(最常见):
//最贴近快排的根本原理(见《算法笔记 胡凡》快排部分)
#include<iostream>
using namespace std ;
const int N = 1e6 + 10 ;
int q[N] , n ;
void quick_sort(int q[] , int l , int r){
if(l >= r) return ;
int pivot = q[l] ;
int i = l , j = r ;
while(i < j ){
while(i < j && q[j] > pivot ) j-- ;//while中必须有i<j ,这个算法要保证i<=j , 不像yxc的那样,可以出现 i>j
q[i] = q[j] ; //交换
while(i < j && q[i] <= pivot ) i++ ;//见最下面的注解
q[j] = q[i] ;
}
q[i] = pivot ;//这一步容易漏,pivot里保留的是原始的q[l]
//运行到这里,i=j , q[j]成为分界点
quick_sort(q , l , i - 1 ) ;
quick_sort(q , i + 1 , r) ;
}
int main()
{
cin >> n ;
for(int i = 0 ; i < n ; i++){
cin >> q[i] ;
}
quick_sort(q , 0 , n - 1);
for(int i = 0 ; i < n ; ++i){
cout << q[i] << ' ' ;
}
}
==注:==
①先动j 指针,后动i 指针,两个while循环有先后。你可以试着反着写 , 以[5,4,3]为例,一个while循环后 , 变成了[5,4,5] , 也就是说q[r]丢失了,被覆盖了 .这是因为,先动i指针,i必定停留在q[l]处,然后使q[r] = q[l] , 而q[r] 没有被pivot备份。
②从小到大排列,则两个while循环里面条件分别为 j:q[j]>pivot,i:q[i]<=pivot ;反之,从大到小排列 , 分别是q[j]<=pivot,q[i]>pivot
举例:[3,4,3] 气死我了,上面两个边界条件,leecode一道题卡了一晚上215. 数组中的第K个最大元素 - 力扣(LeetCode)
③如果考虑到pivot选择q[l]耗时 , 也可以选其他的 , 但要注意先swap(q[l],q[l+r>>1]) , 再 pivot=q[l] 也是考虑到值被覆盖的问题 。这部分《算法笔记 胡凡》也有讲
快速选择
#include<iostream>
#include<vector>
using namespace std ;
const int N = 1e6 + 10 ;
vector<int> nums ;
int quick_select (vector<int>& nums , int l , int r , int k){
if(l >= r) return nums[l] ; //锁定成为一个数,l=r ,该数就是topk
int i = l - 1 , j = r + 1 ;
//int x = nums[(l + r) >> 1] ; //速度快
int x = nums[l] ;
while(i < j )
{
do i++ ; while(nums[i] > x ) ;//从大到小排列
do j-- ; while(nums[j] < x ) ;
if (i < j ) swap(nums[i] , nums[j]) ;
}
//q[j]成为分界点
int len = j - l + 1 ;
if (k <= len ) //Top K位于Top 1 到 Top len 之间
return quick_select(nums , l , j , k) ;
else return quick_select(nums , j + 1 , r , k - len ) ;
}
class Solution {
public:
int quick_select(vector<int>& nums , int l , int r , int k){
int i = l , j = r ;
if(l >= r) return nums[l] ;
int pivot = nums[l] ;
//int tmp = nums[l] ;
while(i < j){
while(i < j && nums[j] <= pivot) j--;
nums[i] = nums[j] ;
while(i < j && nums[i] > pivot) i++ ;
nums[j] = nums[i] ;
}
nums[i] = pivot ;
int len = j - l + 1 ;
if(k <= len) return quick_select(nums , l , j , k);
else return quick_select(nums , j + 1 , r , k - len ) ;
}
int findKthLargest(vector<int>& nums, int k) {
return quick_select(nums , 0 , nums.size() - 1 , k) ;
}
};
归并排序(merge sort)
#include<iostream>
using namespace std ;
const int N = 1e5 + 10 ;
int n , q[N] ;
int tmp[N] ;
void merge_sort(int q[] , int l , int r ){
if(l >= r) return;
int i = l , mid = l + ( r - l >> 1 ) , k = 0 ;
int j = mid + 1 ;
merge_sort(q , l , mid ) ;
merge_sort(q , mid + 1 , r ) ;
while(i <= mid && j <= r ){
if( q[i] <= q[j] ) tmp[k++] = q[i++] ;
else tmp[k++] = q[j++] ;
}
while(i <= mid) tmp[k++] = q[i++] ;
while(j <= r) tmp[k++] = q[j++] ;
for(int i = l , j = 0 ; i <= r ; i++,j++) q[i] = tmp[j] ;
//上面tmp到q的复制,这样写行吗?
//for(int i = 0 , j = 0 ; i <= n ; i++ , j++ ) q[i] = tmp[j];
//乍一看,主函数里调用merge_sort时,l=0,r=n啊,不是一样的吗
//但是你要注意到,merge_sort里面还套了很多娃,这些娃的l,r就不是0,n了
//所有写的程序一定要有通用性、可移植性,尽量引用实参。
}
int main()
{
cin >> n ;
for(int i = 0 ; i < n ; ++i) scanf("%d" , &q[i] ) ;
merge_sort(q , 0 , n - 1) ;
for(int i = 0 ; i <n ; ++i ) printf("%d " , q[i]) ;
}
二分查找(binary search)
class Solution {
public:
int search(vector<int>& nums, int target) {
int l = 0 , r = nums.size() - 1 ;
while(l <= r){
int mid = (l + r) >> 1 ;
if(nums[mid] == target) return mid ;
else if(nums[mid] > target) r = mid - 1;
else l = mid + 1 ;
}
return -1 ;
}
};
#include<iostream>
using namespace std ;
int main()
{
double n , res ;
cin >> n ;
double l = -1000 , r = 1000 ;
while(r - l >= 1e-7){
res = (l + r) / 2 ;
if(res * res * res >= n) r = res ;
else l = res ;
}
printf("%lf" , res);
}
高精度计算
Add
//Add高精度加法
#include<iostream>
#include<vector>
using namespace std ;
vector<int> Add (vector<int>& A , vector<int>& B)
{
vector<int> C ;
int t ;
for(int i = 0 ; i < A.size() || i < B.size() ; ++i ){
if(i < A.size() ) t += A[i] ;
if(i < B.size() ) t += B[i] ;
C.push_back( t % 10 ) ;
t /= 10 ;
}
if(t) C.push_back(1) ;
return C ;
}
int main()
{
string a , b ;
cin >> a >> b ;
vector<int> A , B ;
for(int i = a.size() - 1 ; i >= 0 ; --i) A.push_back(a[i] - '0') ;
for(int i = b.size() - 1 ; i >= 0 ; --i) B.push_back(b[i] - '0') ;
auto C = Add( A , B ) ;
for(int i = C.size() - 1 ; i >= 0 ; --i ) printf("%d" , C[i]) ;
}
Sub
//高精度减法
#include<iostream>
#include<vector>
using namespace std ;
bool cmp (vector<int>& A , vector<int>& B){
if(A.size() != B.size()) return A.size() > B.size() ;
for(int i = 0 ; i < A.size() ; ++i) {
if(A[i] != B[i]) return A[i] > B[i] ;
}
return true ;
}
vector<int> Sub (vector<int>& A , vector<int>& B)
{
vector<int> C ;
int t = 0 , s = 0 ; //t 记录借位
for(int i = 0 ; i < A.size() ; i++){
s = A[i] - t ;
if(i < B.size()) s -= B[i] ;
C.push_back( (s + 10) % 10 ) ;
t = (s >= 0) ? 0 : 1 ;
}
while( C.size() > 1 && C.back() == 0 ) C.pop_back() ;//去除前导0
return C ;
}
int main()
{
string a , b ;
cin >> a >> b ;
vector<int> A , B ;
for(int i = a.size() - 1 ; i >= 0 ; --i) A.push_back(a[i] - '0') ;
for(int i = b.size() - 1 ; i >= 0 ; --i) B.push_back(b[i] - '0') ;
if(cmp(A , B)){
auto C = Sub(A , B) ;
for(int i = C.size() - 1 ; i >= 0 ; --i) printf("%d" , C[i]);
}
else{
auto C = Sub(B , A) ;
printf("-");
for(int i = C.size() - 1 ; i >= 0 ; --i) printf("%d" , C[i]);
}
}
Mul
//Mul
//这里的乘法是把乘数b当成一个整体计算的 , 仔细体会
#include<iostream>
#include<vector>
using namespace std ;
vector<int> Mul(vector<int>& A , int b){
vector<int> C ;
int t = 0 ;
for(int i = 0 ; i < A.size() || t ; ++i){ //此处或上t , 表示若A最高位乘b得到一个多位数,此时t要表示多次进位
if(i < A.size()) t += A[i] * b ;
C.push_back(t % 10) ;
t /= 10 ;
}
return C ;
}
int main()
{
string a ; int b ; vector<int> A ;
cin >> a >> b ;
for(int i = a.size() - 1 ; i >= 0 ; --i) A.push_back(a[i] - '0') ;
auto C = Mul(A , b) ;
for(int i = C.size() - 1 ; i >= 0 ; --i) printf("%d" , C[i]);
}
Div
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std ;
vector<int> Div (vector<int> A , int b , int &r){
vector<int> C ;
for(int i = A.size() - 1 ; i >= 0 ; --i){
r = r * 10 + A[i] ;
C.push_back(r / b);
r %= b ;
}
reverse(C.begin() , C.end()) ;
while(C.size() > 1 && C.back() == 0) C.pop_back() ;
return C ;
}
int main()
{
string a ; int b ; vector<int> A , C ;
cin >> a >> b ;
for(int i = a.size() - 1 ; i >= 0 ; i--) A.push_back(a[i] - '0');
int r ;//余数
C = Div(A , b , r) ;
for(int i = C.size() - 1 ; i >= 0 ; i--) cout << C[i] ;
cout << "......" << r ;
}
==这道题我差不多折腾了一天==
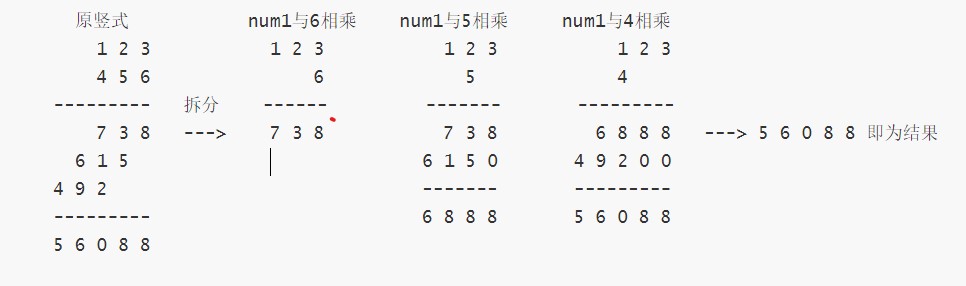
方法一. 模拟乘法计算
//模拟乘法计算
#include<iostream>
#include<string>
#include<algorithm>
using namespace std ;
string Mul(string& A , int b){
int t = 0 ;
string C ;
for(int i = A.size() - 1 ; i >= 0 || t ; --i){
if(i >= 0) t +=( ( A[i] - '0' ) * b ) ;
C.push_back(t % 10 + '0') ;
t /= 10 ;
}
reverse(C.begin() , C.end() ) ;
return C ;
}
string Add(string& A , string& B){
int t = 0 ;
string C ;
for(int i = A.size() - 1 , j = B.size() - 1 ; i >= 0 || j >= 0 ; i-- , j--){
if(i >= 0) t += A[i] - '0' ;
if(j >= 0) t += B[j] - '0' ;
C.push_back(t % 10 + '0') ;
t /= 10 ;
}
if(t) C.push_back('1') ;
reverse(C.begin() , C.end()) ;
return C ;
}
string multiply(string num1, string num2) {
if(num1 == "0" || num2 == "0") return "0" ;
string sum = "0" , tmp;
int count ;
for(int i = num2.size() - 1 ; i >= 0 ; i-- ){
count = num2.size() - i - 1 ;//记录要加几个零(找规律)
tmp = Mul(num1 , num2[i] - '0') ;
while( count-- ) tmp.push_back('0') ;//补上0再加
sum = Add(sum , tmp) ;
}
return sum ;
}
int main()
{
string A , B ;
cin >> A >> B ;
auto C = multiply(A , B) ;
for(int i = 0 ; i < C.size() ; i++ ) printf("%d" , C[i] - '0');
}
方法二. 优化乘法计算

以123×45为例,可知结果res最大尺寸为5 , 123中各数字索引index分别为0 ,1 ,2 , 而45中4、5索引分别为0,1 ,将5与3相乘得15,15是加在res[3]、res[4]上的;2乘5得10,10分别加在res[2]、res[3]上……我们可以找到规律:num1中num1[i]×num2[j],所得积得各位、十位分别加在res[i+j+1]和res[i+j]上。
class Solution {
public:
string multiply(string num1, string num2) {
if(num1 == "0" || num2 == "0") return "0" ;
int size1 = num1.size() , size2 = num2.size() ;
int t ;
vector<int> res(size1 + size2 , 0) ;
string num3 ;
for(int i = size1 - 1 ; i >= 0 ; --i){
for(int j = size2 - 1 ; j >= 0 ; --j){
//非常巧妙
t = (num1[i] - '0') * (num2[j] - '0') + res[i + j + 1];
res[i + j + 1] = t % 10 ;
res[i + j] += t / 10 ;
}
}
reverse(res.begin() , res.end());
while(res.size() > 1 && res.back() == 0) res.pop_back() ;
for(int i = res.size() - 1 ; i >= 0 ; i--) num3.push_back(res[i] + '0') ;
return num3 ;
}
};
==Tips:==
重新看时可能会疑惑:res[i + j]如果产生了进位,那以上代码是如何处理进位得呢?我之前尝试用变量记录进位,但不太好写,此处是这样处理的:res[i+j]+=t/10 ,运算后res[i + j] > 10 了,比如res[i + j] = 13 , 不管 ,就让res[i + j] =13 , 在下一个循环时,前一个循环res[i + j ] 变成了当前循环的res[i + j + 1] , 若t=7×8+res[i+j+1]=56+13=69 ,再经过res[i + j + 1] = t % 10 = 9 后, 上个循环的res[i + j] = 13就经过处理变成了9,从而处理了进位。
(建议用gdb单步执行987×65来理解这种神奇的算法。
前缀和
一维前缀和
前缀和即:Si=a1+a2+……+ai,S0=0
利用前缀和的性质,用来求一段[l,r]的数组和Sr−Sl−1
前缀和的初始化:S0=0,Si=Si−1+ai
#include<iostream>
using namespace std ;
const int N = 1e5 + 10 ;
int a[N] , S[N] ;
int main()
{
int m , n ;
scanf("%d %d" , &n ,&m);
//注意数组下标是从1开始的
for(int i = 1 ; i <= n ; i++) scanf("%d" , &a[i]);
//S[0] = 0 , 全局变量
for(int i = 1 ; i <= n ; i++) S[i] = S[i - 1] + a[i] ;
while(m--){
int l , r ;
scanf("%d %d" , &l , &r);
printf("%d\n" , S[r] - S[l - 1]);
}
}
二维前缀和
初始化:S0,0=0,Si,j=Si−1,j+Si,j−1−Si−1,j−1+ai,j
求值:Sx2,y2−Sx2,y1−1−Sx1−1,y2+Sx1,y1
#include<iostream>
using namespace std ;
const int N = 1010 ;
int a[N][N] , S[N][N] ;
int main()
{
int m , n , q ;
scanf("%d %d %d" , &n , &m , &q);
for(int i = 1 ; i <= n ; ++i)
for(int j = 1 ; j <= m ; ++j)
scanf("%d" , &a[i][j]);
for(int i = 1 ; i <= n ; ++i)
for(int j = 1 ; j <= m ; ++j)
S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + a[i][j] ;
while(q--){
int x1 , y1 , x2 , y2 ;
scanf("%d %d %d %d" , &x1 ,&y1 ,&x2 , &y2);
printf("%d\n" , S[x2][y2] - S[x1 - 1][y2] - S[x2][y1 - 1] + S[x1 - 1][y1 - 1]) ;
}
}
差分
一维差分
差分是前缀和的逆运算,给定数组a1,a2,a3……an,可找到数组b1,b2……bn其中bi=ai−ai−1 ,称bn是an的差分 , 且an是bn的前缀和,即ai=b1+b2+……bi
利用这一性质,可以简化操作:对a_n数组下标索引区间[l,r]中元素加c , 即al+c,al+1+c,……,ar+c
我们只需将bl+=c,br+1−=c , 即只需O(1)的复杂度
#include<iostream>
using namespace std ;
const int N = 1e5 + 10 ;
int a[N] , b[N] ;
int main()
{
int n , m ;
scanf("%d %d" , &n , &m) ;
for(int i = 1 ; i <= n ; i++) scanf("%d" , &a[i]);
for(int i = 1 ; i <= n ; i++) b[i] = a[i] - a[i - 1] ;
while(m--){
int l , r , c ;
scanf("%d %d %d" , &l , &r , &c);
b[l] += c ;
b[r + 1] -= c ;
}
for(int i = 1 ; i <= n ; i++){
a[i] = a[i - 1] + b[i] ;
printf("%d " , a[i]) ;
}
}
二维差分
差分矩阵构造方法:bi,j=ai,j−ai−1,j−ai,j−1+ai−1,j−1
在[(x1,y1),(x2,y2)]的子矩阵中加c :
$$
b_{x_1,y_1} \ += c ; \
b_{x_1,y_2+1}\ -= c ;\
b_{x_2+1,y_1} \ -= c;\
b_{x_2+1,y_2+1} \ += c ;\
$$
由差分矩阵得前缀和矩阵:$a_{i,j} = b_{i,j}+ a_{i-1 , j} + a_{i,j-1} - a_{i-1,j-1}$
#include<iostream>
using namespace std ;
const int N = 1010 ;
int a[N][N] , b[N][N] ;
int main()
{
int n , m , q ;
cin >> n >> m >> q ;
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= m ; j++)
scanf("%d" , &a[i][j]) ;
for(int i = 1 ; i <= n ; i++)
for(int j = 1 ; j <= m ; j++)
b[i][j] = a[i][j] - a[i - 1][j] - a[i][j - 1] + a[i - 1][j - 1] ;
while(q--){
int x1 , y1 , x2 , y2 , c ;
cin >> x1 >> y1 >> x2 >> y2 >> c ;
b[x1][y1] += c ;
b[x1][y2 + 1] -= c ;
b[x2+1][y1] -= c ;
b[x2 + 1][y2 + 1] += c ;
}
for(int i = 1 ; i <= n ; i++){
for(int j = 1 ; j <= m ; j++){
a[i][j] = b[i][j] + a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] ;
cout << a[i][j] << ' ' ;
}
cout << endl ;
}
}


加油!!!
加油!!!