概况：本篇文章会介绍Nim游戏及其变形与SG函数

蒟蒻代码较丑，所以放到最后了，毕竟思路最重要
在此之前：
1.异或运算，数学符号为$\oplus$，$a\oplus b$为在二进制下，对比$a$与$b$每一位的数，若不同，则异或结果中该位为1，否则为0。可以理解为不进位的二进制加法。
2.本文章中所有蓝字系超链接，可以点击跳转到相应题目

1.Nim游戏

本题可以用异或运算来解决
怎么样，是不是很神奇？

设有$n$堆石子，每堆分别有$a_1,a_2,…,a_n$个石子

记$x=a_1\oplus a_2\oplus …\oplus a_n$

则若$x=0$，则先手必败，否则必胜

怎么解释？

1.因为每次只能从中取出大于0的石子数，所以不难看出这个游戏是有尽头的

2.证明：若$x≠0$，则一定存在一种取法，使得取完后$x=0$

3.证明：若$x=0$，则无论下一步怎么取，都会使得$x≠0$

4.游戏结束时，$a_1\oplus a_2\oplus …\oplus a_n=0\oplus 0\oplus …\oplus 0=0$

对于2.的证明：

记$x$二进制表示中最高位(1)为第k位，则$a_1\oplus a_2\oplus …\oplus a_n$中至少有一个数(记为$a_i$)，它的二进制表示中第k位是1
(否则若所有的数第k位都是0，那么$x$的第k位必定也是0)

则$a_i\oplus x<a_i$必定成立
(因为$a_i$二进制表示的第k位从1变为0了，而这是x所能影响到的最高一位，所以无论$1$~$k-1$位如何变化，都不会影响$a_i\oplus x<a_i$这一结果)

则显然$a_i-(a_i\oplus x)>0$，而这就是我们作为先手要从第i堆取走的石子数
(因为$a_i-(a_i\oplus x)>0$，所以无论如何这种取法都是正确的)

当取走这些石子时，第i堆只剩下$a_i-(a_i-(a_i\oplus x))=a_i\oplus x$个石子

此时$a_1\oplus a_2\oplus …\oplus a_i\oplus x\oplus …\oplus a_n=x\oplus x=0$，证毕

对于3.的证明(反证法)：

假设能从第任意堆$a_i$中取走$a_i’$个石子，使得前后都满足$x=0$，
则$a_1\oplus a_2\oplus …\oplus a_n=a_1\oplus a_2\oplus …\oplus (a_i-a_i’)\oplus …\oplus a_n=x=0$
则由消去律得$a_i=a_i-a_i’$，即$a_i’=0$，与规则矛盾，故则无论怎么取，都会使得$x≠0$，证毕

综合以上四条，我们可以得到当每个人都采用最优解时，石子的总个数会不断减少，$x$会在0和正整数之间反复横跳，而早晚会有$x=0$且没有石子的情况，此时轮到谁谁就输了

由此反推可知方法与判断的正确性

SG函数

在此之前，先引入一个必要的函数mex

mex($A$)表示不属于集合$A$的最小自然数，其中集合$A$中的元素都是自然数

如mex{0,1,2,4}=3、mex{2,3,5}=0

SG函数的定义：

在有向图游戏中，对于每个节点x，设从x出发有k条有向边，分别到达节点$y_1,y_2,…,y_k$，
则SG(x)=mex(SG($y_1$),SG($y_2$),…SG($y_k$))
没有出边的顶点，即终点，的SG值为0，即SG(终点)=0

注:终点SG值一定为0，但SG值为0的不一定只是终点

如：

SG函数满足以下性质：

对于一个SG(x)$=0$的顶点x，它的所有前驱和后继y都满足SG(y)$≠0$
对于一个SG(x)$≠0$的顶点x，必定存在一个后继y，满足SG(y)$=0$

通过这些性质，我们就可以判断谁胜谁败了，具体地：
对于游戏$G$，SG($G$)$=0$意味着$G$的所有后继SG值都不是0，而这又意味着其所有后继的后继的SG值必定有0，作为执行者，我们只要每次都选SG值为0的情况就可以了，这样我们留给对手的只有SG=0的情况，这样输的总会是对方。

由此，我们可以得出，对于一个游戏$G$，SG($G$)$=0$意味着先手必败，否则必胜

是不是很熟悉？是不是和Nim游戏中x的情况几乎一样？
其实仔细研究不难发现，在Nim游戏中每一堆都是一个Nim游戏的子游戏，而由于Nim的特殊规定，使得每一个子游戏的SG值是其本身石子数，例如：

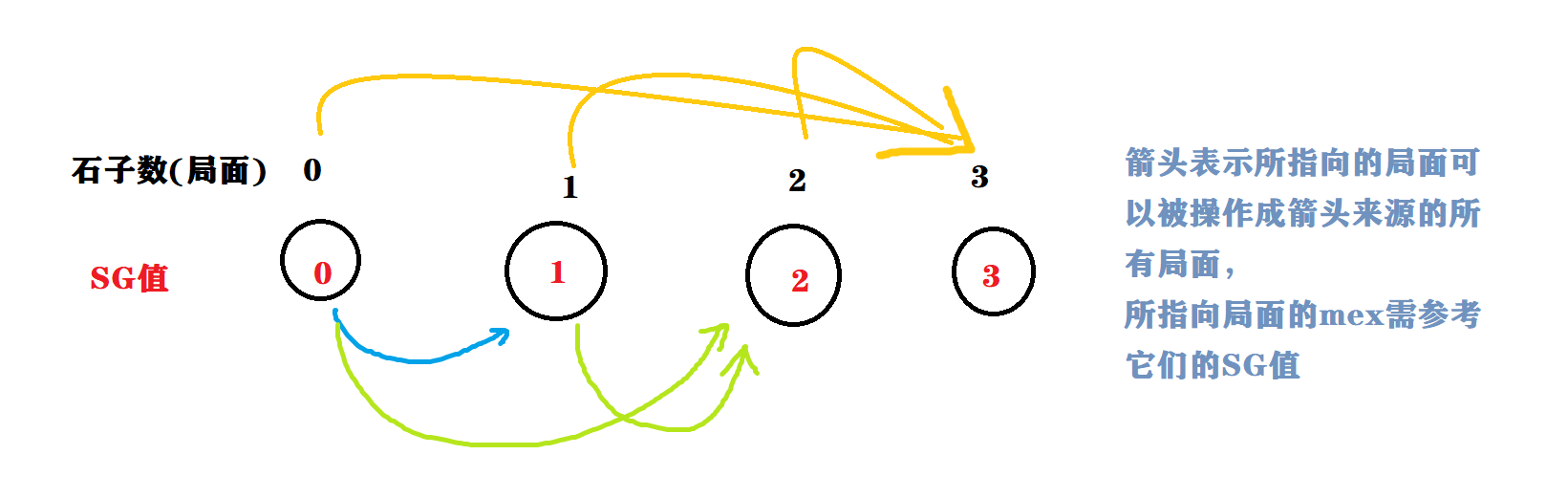
而对于整个Nim游戏，只需要对所有SG值进行异或运算即可，这个我们已经证明过。

由此，我们不难得出：原游戏的SG函数值是它的所有子游戏的SG函数值的异或

那么接下来，让我们用SG函数解决 拆分游戏吧

先解释一下题意，也是很多人看不懂的地方(其实我一开始也懵逼了):
题目让我们随便选择一堆石子，把它拿走，然后创造两堆石子，每一堆个数都得小于原堆个数，可以是0个石子。而不是把选择的石子分为两份放到别的石子堆中啊喂！！

我们不难看出，对于整个游戏，它分为了很多子游戏，即每个石子堆，每个子游戏都有很多的解法，都可以造成很多局面。而对于每个子游戏，求出它们的SG值，进行异或运算就可以看出谁嬴谁输了。这个我们已经在上文中提到其正确性了。

而对于每个子游戏的SG值，可以通过记忆化搜索查找。每个子游戏进行一次操作后，都会生成两个新堆，相当于拿走一个，放了两个——多了一个堆。而对于每一堆，又可以看成一个新的游戏(子游戏里的子游戏？)，把它分为两个子游戏，取异或即可。

CODE-Nim游戏

#include <iostream>

using namespace std;

int main()
{
    int n, a;
    int res = 0;

    cin >> n;

    while(n -- )
    {
        cin >> a;
        res ^= a;
    }

    if(res) cout << "Yes";
    else cout << "No";

    return 0;
}

CODE-拆分游戏

#include <cstring>
#include <iostream>
#include <unordered_set>

using namespace std;

const int N=110;
int f[N]; //储存sg值
int n, x;


int sg(int x)
{
    if(f[x] != -1) return f[x];

    unordered_set<int> S;

    for(int i = 0; i < x; i ++ )
        for(int j = 0; j <= i; j ++ )
            S.insert(sg(i) ^ sg(j));

    for(int i = 0; ; i ++ )
        if(!S.count(i)) return f[x] = i;
}


int main()
{
    memset(f, -1, sizeof f);

    int res = 0;

    cin >> n;

    while(n -- )
    {
        cin >> x;

        res ^= sg(x);
    }

    if(res) cout << "Yes";
    else cout << "No";

    return 0;
}