深度优先搜索思想
深度优先搜索(DFS)思想:一直往深处走,直到找到解或走不下去为止。
DFS框架:
DFS(deep, ...) { // deep代表目前DFS的深度
if (找到解 || 走不下去了) { // DFS出口
...
return;
}
枚举下一种情况,DFS(deep + 1, ...);
}
“枚举下一种情况”与”找DFS的出口”是深度优先搜索的关键
【例题】自然数和分解
题目链接: 自然数和分解
题目大意:把自然数$N$分解为若干个大于 $0$ 自然数之和,输出方案数。
样例解释:$5$可以拆分成$[1, 1, 1, 1, 1], [1, 1, 1, 2], [1, 1, 3], [1, 2, 2], [1, 4], [2, 3], [5]$,一共有$7$种方案。
【分析】
提问:先思考如何将一个数$n$拆分成$2$个数
回答:枚举小于等于$n$的数$a, b = n - a$
这题其实就是在枚举每一种拆分的情况,将$n$拆分成$a, b$,当前的$a, b$算一种方案,
如果$b$不等于$0$,那就还需要重复拆分步骤,直到不能拆。
再来看看我们的$DFS$框架:
提问:如果用$DFS$去拆分,这里$DFS$出口应该是什么?
回答:当前的数等于$0$
如何去枚举?和前面所说把$n$拆成两个数的步骤一样
核心代码
int ans = 0;
// 每次枚举的数从x开始,这样保证拆分方案不会重复
void DFS(int n, int x) {
if (n == 0) { // n = 0, 不能再拆分,找到出口
ans++;
return;
}
// 从x开始枚举,把n拆分成a与n-a
for (int a = x; a <= n; ++a) {
DFS(n - a, a);
}
}
int main() {
int n;
cin >> n;
DFS(n, 1);
cout << ans << '\n';
}
回溯算法思想
回溯算法思想:回溯算法也是遵循深度优先的算法,也叫做试探法。枚举尝试过程中寻找问题的解,
当发现已不满足求解条件时,就”回溯返回”,尝试别的路径。
与深度优先搜索相比:
相同点:一步走到底
不同点:在枚举前标记当前的状态,枚举结束后取消标记
回溯算法框架:
DFS(deep, ...) { // deep代表目前DFS的深度
if (找到解 || 走不下去了) { // DFS出口
...
return;
}
枚举下一种情况,做好标记,
DFS(deep + 1, ...);
取消标记。
}
除了”枚举下一种情况”与”找DFS的出口”以外,回溯算法还需要”做标记”
【例题】全排列问题
题目链接: 全排列问题
题目大意:输出自然数 $1$ 到$n$ 所有不重复的排列,即 $n$ 的全排列,要求所产生的任一数字序列中不允许出现重复的数字。
提问:如果$n=3$,用for循环如何做这一题?
回答:写三个for循环,每个for循环从1遍历到n,然后依次输出
核心代码
for (int i = 1; i <= 3; ++i) {
for (int j = 1; j <= 3; ++j) {
if (i == j) continue;
for (int k = 1; k <= 3; ++k) {
if (i == k || j == k) continue;
cout << i << " " << j << " " << k << '\n';
}
}
}
【分析】
由于这里$n$是不确定的,所以不能用for循环直接模拟这个过程。枚举的过程需要判断标记已经使用过的数字。
每层for循环做的事情大致都差不多,并且是一层套一层。
能否用回溯框架改下这段代码?
for (int i = 1; i <= 3; ++i) {
for (int j = 1; j <= 3; ++j) {
if (i == j) continue;
for (int k = 1; k <= 3; ++k) {
if (i == k || j == k) continue;
cout << i << " " << j << " " << k << '\n';
}
}
}
【分析】
再看看我们的回溯算法框架:
提问:出口是什么?
回答:当$deep$等于$n+1$
提问:为什么是$n+1$?
回答:当$deep$等于$n+1$时,在执行$if$语句时已经枚举了$n$个数,满足要求
核心代码
int ans[10]; // 记录枚举的数字
bool vis[10]; // 记录数字是否被枚举过
int n;
void DFS(int n) {
if (deep == n + 1) {
// 输出答案
for (int i = 1; i <= n; ++i) {
cout << " " << ans[i];
}
cout << '\n';
return;
}
for (int i = 1; i <= n; ++i) {
if (vis[i] == true) // 如果访问过,不再访问
continue;
vis[i] = true; // 做标记表示已经访问过
ans[deep] = i; // 记录当前枚举的数字
DFS(deep + 1); // 继续下一层的枚举
vis[i] = false; // 取消标记
}
}
【例题】 组合的输出
首先我们先回忆一下如何递归实现二进制枚举(子集枚举),假设我们需要找到一个长度为 $n$ 的序列 $a$ 的所有子序列,代码框架是这样的:
vector<int> ans;
void dfs(int x) {
if (x == n+1) {
// 输出答案
return;
}
// 考虑选择当前位置
ans.push_back(x);
dfs(x+1);
dfs(x+1);
ans.pop_back();
// 考虑不选择当前位置
dfs(x+1);
}
dfs(x) 参数表示中的 $x$ 表示当前位置是 $x$。原序列的每个位置在答案中的状态有被选中和不被选中两种。在进入 dfs(x) 之前 [1, x-1] 位置的状态是确定的,而 [x, n] 内位置的状态是不确定的,dfs(x) 需要确定 $x$ 位置的状态,然后求解子问题 dfs(x+1)。 对于 $x$ 位置,我们需要考虑 $a[x]$ 取或者不取,如果取,我们需要把 $a[x]$ 我们需要把 $a[x]$ 放入答案数组 $ans$ 中,再执行 dfs(x+1);如果不取,则执行 dfs(x+1)。在整个递归调用的过程中,$x$ 是从小到大递增的,当 $x$ 增加到 $n+1$ 时,输出答案并终止递归。可以看出二进制枚举的复杂度是 $O(2^n)$。
vector<int> ans;
void dfs(int x) {
if (ans.size() == r) {
rep(i, n) cout << ' ' << ans[i];
puts("");
}
// x == n+1 时结束递归
if (x == n+1) {
return;
}
// 考虑选择当前位置
ans.push_back(x);
dfs(x+1);
dfs(x+1);
ans.pop_back();
// 考虑不选择当前位置
dfs(x+1);
}
这个时候我们可以做一个剪枝,记 $ans$ 的大小为 $s$,未确定状态的区间 $[x, n]$ 的长度为 $t$,如果 $s+t < r$,那么即使 $t$ 个都被选中,也不可能构造出一个长度为 $r$ 的序列,故这种情况就没有必要继续向下递归,即我们可以在每次递归开始前做一次这样的判断:
if (ans.size() + (n-x+1) < r) return;
于是代码就变成了这样:
vector<int> ans;
void dfs(int x) {
if (ans.size() + (n-x+1) < r) return;
if (ans.size() == r) {
rep(i, n) cout << ' ' << ans[i];
puts("");
}
// x == n+1 时结束递归
if (x == n+1) {
return;
}
// 考虑选择当前位置
ans.push_back(x);
dfs(x+1);
dfs(x+1);
ans.pop_back();
// 考虑不选择当前位置
dfs(x+1);
}
至此,其实我们已经得到了一个时间复杂度为 $O(\binom{n}{r})$ 的组合枚举,由于每次输出答案的复杂度为 $O(r)$,故这里的时间复杂度为 $O(\binom{n}{r} \times r)$,但是我们还可以进行优化代码。在上面这份代码中有三个 if 判断,其实第三处的 if 是可以被删除的。因为:
- 首先,$x=n+1$ 的时候,一定不可能出现 $s > r$,因为自始至终 $s$ 绝不可能大于 $r$,它等于 $r$ 的时候就会被第二处
if输出答案并返回 - 如果 $x = n+1$ 的时候 $s=r$,它也会被第二处
if输出答案并返回 - 如果 $x=n+1$ 的时候 $s < k$,一定会在 $x < n+1$ 的某个位置的时候发现 $s+t < r$,它也会被第一处
if剪枝。
因此,第三处 if 可以删除。最终我们得到了如下代码:
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using std::cin;
using std::cout;
using std::function;
using std::vector;
int main() {
int n, r;
cin >> n >> r;
vector<int> ans;
function<void(int)> dfs = [&](int x) {
if (ans.size() + (n - x + 1) < r)
return;
if (ans.size() == r) {
rep(i, r) cout << ' ' << ans[i];
puts("");
return;
}
// 考虑选择当前位置
ans.push_back(x);
dfs(x + 1);
ans.pop_back();
// 考虑不选当前位置
dfs(x + 1);
};
dfs(1);
return 0;
}
【例题】$N$皇后问题
题目链接: N皇后问题
题目大意:在一张$N*N$的棋盘上放置$N$个皇后($n \leqslant 10$)而彼此不受攻击(即在棋盘的任一行,任一列和任一对角线上不能放置$2$个皇后),编程求解方案总数。
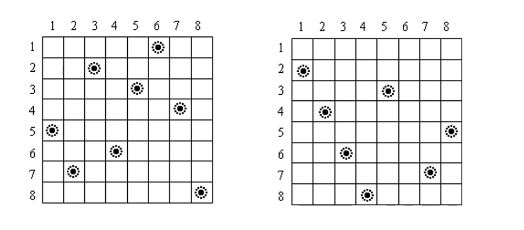
分析:问题的关键在于如何判定某个皇后所在的行、列、斜线上是否有别的皇后;
可以从矩阵的特点上找到规律:
- 如果在同一行,则行号相同
- 如果在同一列,则列号相同
- 如果同在$/$斜线上的行列值之和相同
- 如果同在\斜线上的行列值之差相同
从下图中可验证:
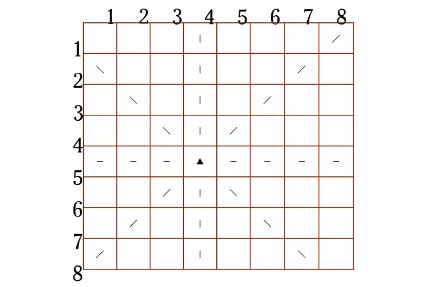
我们可以用一个$position[i]$记录第$i$个皇后,放在$i$行的第$position[i]$位置上。
如果该位置可以被放置,那么这个皇后必然和$position[1] \sim position[i-1]$的皇后不冲突。
则可放置,并进行下一层的搜索。
C++ 代码
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using std::vector;
using std::function;
int main() {
int n;
cin >> n;
int ans = 0;
vector<int> position(n+1);
function<void(int)> dfs = [&](int x) {
if (x == n+1) {
ans++;
return;
}
for (int i = 1; i <= n; ++i) { // 列
// 尝试第 x 行的皇后能否放在第 i 列上
bool ok = true;
for (int j = 1; j < x; ++j) { // 行
// 判断当前 x 行 i 列如果放置了皇后,是否会跟前面的皇后冲突
if (position[j] == i or position[j]+j == x+i or position[j]-j == i-x) {
ok = false;
break;
}
}
if (ok) {
position[x] = i;
dfs(x+1);
}
}
};
dfs(1);
cout << ans << '\n';
return 0;
}
优化:
#include <bits/stdc++.h>
using std::cin;
using std::cout;
using std::function;
int position[20];
bool col[20], line1[30], line2[30];
int main() {
int n;
cin >> n;
int ans = 0;
function<void(int)> dfs = [&](int x) {
if (x == n+1) {
ans++;
return;
}
for (int i = 1; i <= n; ++i) { // 列
// 尝试第 x 行的皇后能否放在第 i 列上
if (col[i] == false and line1[x+i] == false and line2[x-i+n] == false) {
position[x] = i;
col[i] = true;
line1[x+i] = true;
line2[x-i+n] = true;
dfs(x+1);
col[i] = false;
line1[x+i] = false;
line2[x-i+n] = false;
}
}
};
dfs(1);
cout << ans << '\n';
return 0;
}
例题: 迷宫
题目大意:在 $N \times N$ 的迷宫内,# 为墙,. 为路,s 为起点,e 为终点,一共 $4$ 个方向可以走。从左上角 $((0, 0)\ ‘s’)$ 位置处走到右下角 $((n-1, n-1) \ ‘e’)$ 位置处,可以走通则输出 YES,不可以走输出 NO
分析:
- 这题本质就是从 $s$ 出发,尝试性的走出每一步,如果能走就走
-
不能走就退回去换个方向走。直到达到终点或者没有点可走。
-
提问:用回溯法,需要标记什么,用什么标记?
- 回答:需要标记已经走过的点,用二维数组标记
- 提问:回溯的出口是什么?
- 回答:所有点已经走过,或者到达终点
- 提问:如何去枚举走的四个方向?
- 回答:$x+1$,$y+0$ 表示向下走,$x-1$,$y+0$ 表示向上走。
$x+0$,$y+1$ 表示向右走,$x+0$,$y-1$ 表示向左走。
C++ 代码
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)
using std::cin;
using std::cout;
using std::string;
using std::vector;
using std::function;
void solve() {
int n;
cin >> n;
vector<string> s(n);
rep(i, n) cin >> s[i];
bool ok = false;
function<void(int, int)> dfs = [&](int i, int j) {
if (i<0 or i>=n or j<0 or j>=n) return;
if (s[i][j] == '#') return;
if (s[i][j] == 'e') {
ok = true;
return;
}
s[i][j] = '#';
dfs(i-1, j); // 向上
dfs(i+1, j); // 向下
dfs(i, j-1); // 向左
dfs(i, j+1); // 向右
// s[i][j] = '.';
};
dfs(0, 0);
if (ok) puts("YES");
else puts("NO");
}
int main() {
int t;
cin >> t;
while (t--) solve();
return 0;
}
总结:
这题与上一题有一些区别:
- 需要判断枚举的边界
- 标记的方式不同
- 不用取消标记
最后提醒
- 搜索即暴力
- 不需要太多剪枝 => 有些剪枝是要花时间算的
- 不需要非常复杂的估价函数 => noip基本不需要复杂的估价函数
- 不需要特别多的算法结合
- 代码不混乱且不是特别长,特别注意不混乱,考场上要能调出来,最好是能写完,看一遍就对了
- 不要抄代码,搜索不自己写没用


感谢大佬指点