bellmam-ford算法与SPFA

这期我们来讲一讲如何处理负边权的最短路断路问题。

一、bellmam-ford算法。

大家放心。
看着这个高大上的名字。
我可以告诉大家，这个算法最难的地方就是这个算法的名字很难拼……
(而且这个算法很傻)
算法过程如下：
先进行n-1次代谢
接着枚举每条边
然后用以前的边更新这个边………………
没了。
唯一的难点就是需要用一个last数组存上次使用的点。
简单说就是备份数组。
但是这里大家要学会一个东西：

memcpy

那么ta是干蛤的呢？
cpy——复制。
备份的时候需要把数组复制一下。

memcpy(last, dist, sizeof dist);

最后我们来看一下bellmam-ford算法的板子。

void bellmamford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    for(int i = 0 ; i < k; i ++)
    {
        for(int j = 0; j < m; j ++)
        {
            auto e = es[j];
            if(dist[e.b] > dist[e.a] + e.w) dist[e.b] = dist[e.a] + e.w;
        }
    }
}

关键这个算法最弱的地方就是——

它存边是用的结构体………………………………………………

但是这个算法有一个特性，就是因为第二次遍历k条边（如上板子），
所以这个算法可以求出有边数限制的最短路。
而其他算法就做不到。
所以，

暴力出奇迹！

我们看一下这道题
题目描述：
给定一个n个点m条边的有向图，图中可能存在重边和自环，边权可能为负数。

请你求出从1号点到n号点的最多经过k条边的最短距离，如果无法从1号点走到n号点，输出impossible。

注意：图中可能 存在负权回路 。

输入格式
第一行包含三个整数n，m，k。

接下来m行，每行包含三个整数x，y，z，表示存在一条从点x到点y的有向边，边长为z。

输出格式
输出一个整数，表示从1号点到n号点的最多经过k条边的最短距离。

如果不存在满足条件的路径，则输出“impossible”。

数据范围

1 ≤ n, k ≤ 500,
1 ≤ m ≤ 10000,

任意边长的绝对值不超过10000。

输入样例：

3 3 1
1 2 1
2 3 1
1 3 3

输出样例：

3

有人可能要问我，啥是负权回路？
就是一个回路的权值和是负数。
如果这个点在1-n的任一条路径上，

最短路就没了

因为每次在那里转一圈最短路-1，可以转无数圈。
但当这个玩意遇到bellmam-ford算法。
火花没撞出来，脑花到“装”出来了，太慢了……
遇到spfa才有用（见后）
好了继续回到正题。
这题的求法应该很弱吧。
直接bellmam-ford一波。
首先写一个struct，存所以的边。

struct e
{
    int a, b, w;
}es[M];

读入所有数，放进es。

cin >> n >> m >> k;
for(int i = 0; i < m; i ++)
{
    int a, b, w;
    cin >> a >> b >> w;
    es[i] = {a, b, w};
} 

bellmam-ford一遍dist数组，别忘记开last数组备份，dist数组存储。
重复一遍板子。

void bellmamford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    for(int i = 0 ; i < k; i ++)
    {
        memcpy(last, dist, sizeof dist);
        for(int j = 0; j < m; j ++)
        {
            auto e = es[j];
            dist[e.b] = min(dist[e.b], last[e.a] + e.w);
        }
    }
}

最后判断一下，如果dist[n]大于一个很大的数，没有最短路，否则有。

if(dist[n] > 0x3f3f3f3f / 2)  cout << "impossible";
else cout << dist[n];

为啥这里是0x3f3f3f3f / 2呢？
因为图中存在负权边。
完整代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<limits.h>
using namespace std;
const int N = 510, M = 10010;
struct e
{
    int a, b, w;
}es[M];
int n, m, k, dist[N], last[N];
void bellmamford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    for(int i = 0 ; i < k; i ++)
    {
        memcpy(last, dist, sizeof dist);
        for(int j = 0; j < m; j ++)
        {
            auto e = es[j];
            dist[e.b] = min(dist[e.b], last[e.a] + e.w);
        }
    }
}
int main()
{
    cin >> n >> m >> k;
    for(int i = 0; i < m; i ++)
    {
        int a, b, w;
        cin >> a >> b >> w;
        es[i] = {a, b, w};
    } 
    bellmamford();
    if(dist[n] > 0x3f3f3f3f / 2)  cout << "impossible";
    else cout << dist[n];
    return 0;
}

二、SPFA

emmspfa其实就是bellmam_ford的优化。

bellmam-ford算法就看起来特别傻。——yxc

回想一下bellmam_ford，直接两重循环暴力（卡出奇迹）
那有些边更新是不一定会变小的。
如果我们优化一下……
SPFA来了
回忆一下前面的更新方式：

dist[b] = min(dist[b], dist[a] + w);

如果dist[a]变小了，dist[b]才一定会变小。
这就是SPFA的突破口。
所以从这里开始优化。
具体思路是：
bfs
首先搞一个队列……

queue<int> q;

那这个队列是干蛤的呢？
存储所有变小的节点。
是否有一种似曾相识的感觉？
有就好了……继续……
然后每次更新点的时候判断一下是否小，小就更新。
当然st数组还是不能少帝~
结合如上叙述以及bellmam_ford的讲解，SPFA的板子就应该很弱了吧。
先初始化一下。

memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
queue<int> q;
q.push(1);
st[1] = true;

接着宽搜标准板子*INF

while(q.size())
{
    int t = q.front();
    q.pop();
    st[t] = false
}

边的遍历相信大家没忘。

for(int i = h[t]; i != -1; i = ne[i])
{
    int j = e[i];
}

接着看一下这个点需不需要更新，也是SPFA里最关键的部分。

if(dist[j] > dist[t] + w[i])
{
    dist[j] = dist[t] + w[i];
}

看一下是否在集合里，在就更新。

if(!st[j])
{
    st[j] = true;
    q.push(j);
}

最后康康有木有最短路。

if(dist[n] == 0x3f3f3f3f) return -1;
return dist[n];

完整の板子：

int spfa()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    queue<int> q;
    q.push(1);
    st[1] = true;
    while(q.size())
    {
        int t = q.front();
        q.pop();
        st[t] = false;
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                if(!st[j])
                {
                    st[j] = true;
                    q.push(j);
                }
            }
        }
    }
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

作者：cht
链接：https://www.acwing.com/activity/content/code/content/354290/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

为了证明是复制的，挂上上面四行。
好了看下板子题。
SPFA求最短路
给定一个n个点m条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你求出1号点到n号点的最短距离，如果无法从1号点走到n号点，则输出impossible。

数据保证不存在负权回路。

输入格式
第一行包含整数n和m。

接下来m行每行包含三个整数x，y，z，表示存在一条从点x到点y的有向边，边长为z。

输出格式
输出一个整数，表示1号点到n号点的最短距离。

如果路径不存在，则输出”impossible”。

数据范围
1≤n,m≤105,
图中涉及边长绝对值均不超过10000。

输入样例：
3 3
1 2 5
2 3 -3
1 3 4
输出样例：
2

有了SPFA，完事！
直接上代码了，也没啥可讲的。

#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, m, e[N], h[N], w[N], ne[N], idx, dist[N];
bool st[N];
void add(int a, int b,int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
int spfa()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    queue<int> q;
    q.push(1);
    st[1] = true;
    while(q.size())
    {
        int t = q.front();
        q.pop();
        st[t] = false;
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                if(!st[j])
                {
                    st[j] = true;
                    q.push(j);
                }
            }
        }
    }
    return dist[n];
}
int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for(int i = 0; i < m; i ++)
    {
        int a,b ,c;
        cin >> a>> b>> c;
        add(a, b, c);
    }
    int t = spfa();
    if(t == 0x3f3f3f3f) cout << "impossible";
    else cout << t;
}

当然如果出题人故意卡成了O(NM)，请用堆优化Dijkstra。

SPFA的应用

第一章bellmam-ford的时候说过SPFA可以判断负欢负环。
这里讲一下。
先来看一下题目：
SPFA判断负环
给定一个n个点m条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你判断图中是否存在负权回路。

输入格式
第一行包含整数n和m。

接下来m行每行包含三个整数x，y，z，表示存在一条从点x到点y的有向边，边长为z。

输出格式
如果图中存在负权回路，则输出“Yes”，否则输出“No”。

数据范围
1≤n≤2000,
1≤m≤10000,
图中涉及边长绝对值均不超过10000。

输入样例：
3 3
1 2 -1
2 3 4
3 1 -4
输出样例：
Yes

来讲一下这道题。
dist[j]表示的是1->j的最短距离。
同时记录另一个东西：cnt数组。
cnt[j]表示的是1->j的边的数量。
每一次这么更新：
首先dist数组：

dist[j] = dist[t] + w[i];

cnt数组是这样更新的：

cnt[j] = cnt[t] + 1;

为啥？
请看图：

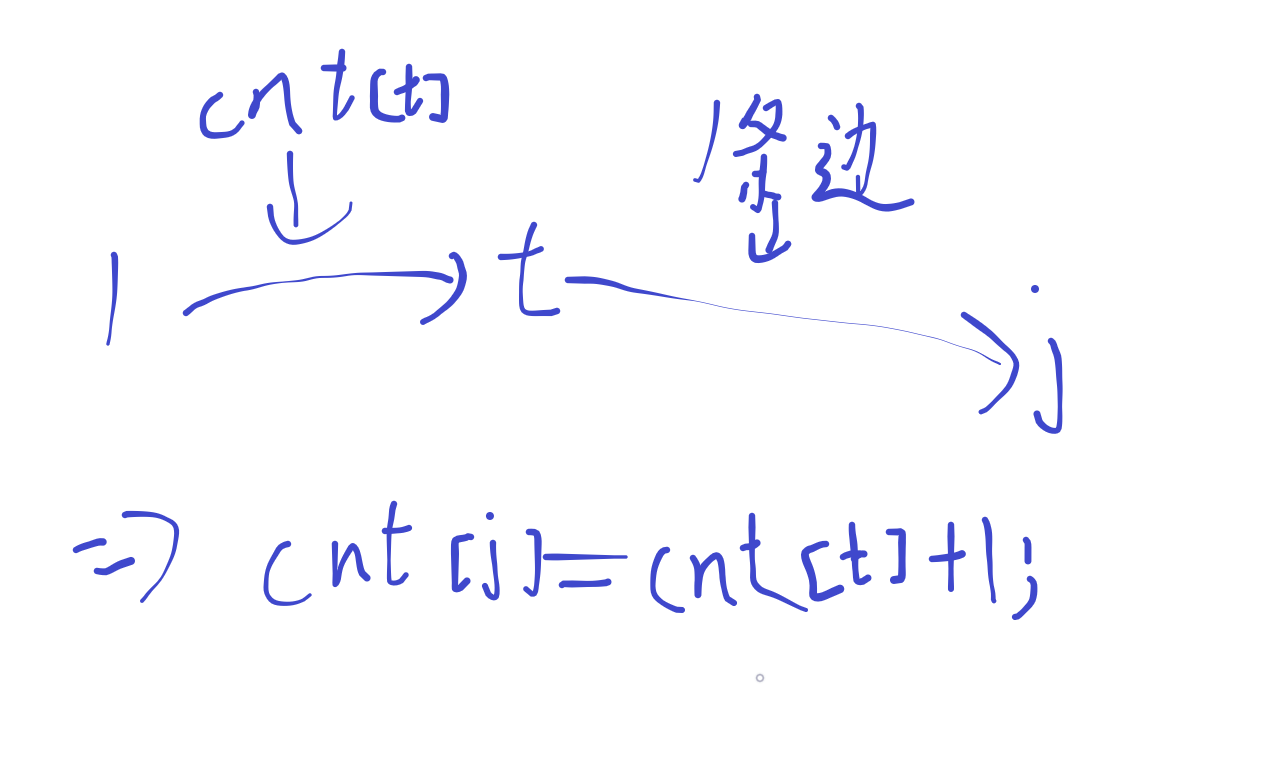
顺便说一句，这个字大家先忍忍，下周二手写板就到了。
我们继续。
如果其中有一次cnt[j] > n:
就说明从1->j经过了n条边
=> 就说明1->j经过了n+1个点。
=> 说明路径上至少两点相同
=> 存在环。
=> 一定会变小，所以环是负权
=> 存在负权边。
这就是SPFA判断负环的重中之重。
然后我们把板子实现一般就行了，这里直接上代码（有点累了，快500行了）。
注意这里初始化的时候要初始化掉所有点。
为啥？
因为负环不一定从1开始。
而且这里不用初始化dist数组了哦。

#include <bits/stdc++.h>
using namespace std;
const int N = 2010, M = N * 5;
int n, m, h[N], e[M], ne[M], w[M], idx, dist[N], cnt[N];
bool st[N];
void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
bool spfa()
{
    queue<int> q;
    for(int i = 1; i <= n; i ++)
    {
        st[i] = true;
        q.push(i);//初始化所有点
    }
    while(q.size())
    {
        int t = q.front();
        q.pop();
        st[t] = false;
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];//更新dist
                cnt[j] = cnt[t] + 1;//更新cnt
                if(cnt[j] >= n) return true;//如果cnt[j] >= n，根据上面的推理说明存在负环
                if(!st[j])
                {
                    st[j] = true;
                    q.push(j);
                }
            }
        }
    }
    return false;
}
int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for(int i = 0; i < m; i ++)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    if(spfa()) puts("Yes");
    else puts("No");
    return 0;
}

好了今天的分享就到这里了。有点累不留作业了。

这里是我的全部分享

下期见，bye~

（500行，好累，下一期说几道bfs，是个视频课没有文字，大家等着吧）