Dijkstra求最短路与其优化

哈罗大家好我是cht，今天我们来讲解一下Dijkstra算法。
（视频最近暂时不录了，比较忙，暑假大概会给大家放出视频）

一、Dijkstra算法是用来干蛤的

这就不得不提到图论了。
基础课里的图论大致可以分为4个部分。

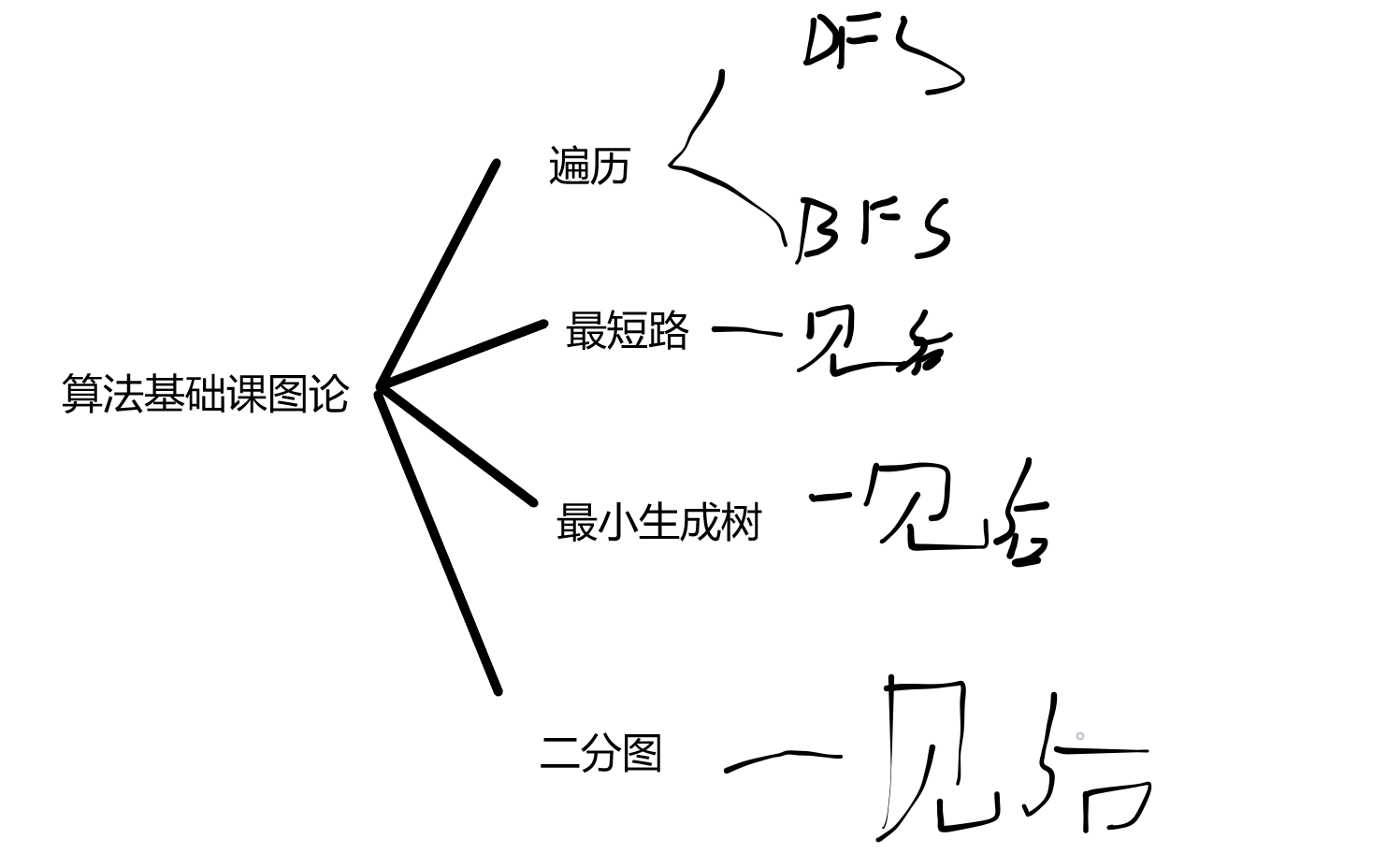
我们图的搜索（遍历）部分已经讲完了。
现在开始讲解第二部分：最短路。
最短路一般分为三种。
1. 多元汇最短路——一般使用Floyd（弗雷德）算法。
2. 没有负权边的单元最短路——一般使用Dijkstra或堆优化Dijkstra。
3. 有负权边的单元最短路——一般使用bellman-ford算法或者SPFA算法。

这里解释一下单元最短路和多元最短路的区别。
单元最短路是指求点1至点n的最短路。
而多元汇最短路是指求任意两点之间的最短路。
今天我们先来讲解一下Dijkstra算法和ta的优化。

二、Dijkstra算法的基本思路

朴素Dijkstra算法的时间复杂度是O(n^2)。
我们先开一个dist数组来存每个点的最短路。
好接下来回忆下怎么用邻接矩阵存储图。

for(int i = 0; i < m; i ++)
{
    int a, b, w;
    cin >> a >> b >> w;
    g[a][b] = min(g[a][b], w);
}

然后我们来说一下dist数组的初始化。
其实非常简单。
首先把所有数赋值：

memset(dist, 0x3f, sizeof dist);

其次把已确定最短路的点标记最短路。

dist[1] = 0;

对，这就完成了初始化。
不过我们还需要开一个st布尔数组来存每个点是否确定最短路。
接着进行n - 1次代谢。

for(int i = 0; i < n - 1; i ++)
{

}

里面总共分为3步。

一、找到目前不在st中距离最近的点。

一个循环完事。
首先这个点必须没有确定最短距离。
然后如果t == -1那也需要更新，如果t不是-1，我们就判断一下这个点是不是没有确定最短距离的距离最近的点。

int t = -1;
for(int j = 1; j <= n; j ++)
{
    if(!st[j] && (t == -1 || dist[t] > dist[j]))
    {            
        t = j;
    }
}

二，把这个点放进st集合。

这个就不用费太多笔墨了。

st[t] = true;

三、用之前的点更新这个点。

for(int j = 1; j <= n; j ++)
    dist[j] = min(dist[j], dist[t] + g[t][j]);

就是这样更新。
代谢结束后需要看一下这个点是不是0x3f3f3f3f。
最后的代码：

if(dist[n] == 0x3f3f3f3f) return -1;
return dist[n];

朴素Dijkstra算法完整模板：

#include<bits/stdc++.h>
using namespace std;
const int N = 510;
int n, m, g[N][N], dist[N];
bool st[N];
int Dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    for(int i = 0; i < n - 1; i ++)
    {
        int t = -1;
        for(int j = 1; j <= n; j ++)
            if(!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        st[t] = true;
        for(int j = 1; j <= n; j ++)
            dist[j] = min(dist[j], dist[t] + g[t][j]);
    }
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

最后我们来看一下朴素Dijkstra算法的习题。
朴素Dijkstra算法

题目描述：

给定一个n个点m条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出1号点到n号点的最短距离，如果无法从1号点走到n号点，则输出-1。

输入格式
第一行包含整数n和m。

接下来m行每行包含三个整数x，y，z，表示存在一条从点x到点y的有向边，边长为z。

输出格式
输出一个整数，表示1号点到n号点的最短距离。

如果路径不存在，则输出-1。

数据范围
1≤n≤500,
1≤m≤105,
图中涉及边长均不超过10000。

输入输出样例：

输入样例：
3 3
1 2 2
2 3 1
1 3 4
输出样例：
3

那这道题直接套一下Dijkstra算法的模板就行了。

#include<bits/stdc++.h>
using namespace std;
const int N = 510;
int n, m, h[N], e[N], ne[N], dist[N], g[N][N];
bool st[N];
int dij()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    for(int i = 0; i< n - 1;i  ++)
    {
        int t = -1;
        for(int j = 1; j <= n; j ++)
        {
            if(!st[j] && (t == -1 || dist[t] > dist[j]))
            {
                t = j;
            }
        }
        st[t]= true;
        for(int j = 1; j <= n; j ++)
            dist[j] = min(dist[j], dist[t] + g[t][j]);
    }
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}
int main()
{
    cin >> n >> m;
    memset(g, 0x3f, sizeof g);
    for(int i = 0; i < m; i ++)
    {
        int a, b, c;
        cin >>a >> b >> c;
        g[a][b] = min(g[a][b], c);
    }
    cout << dij();
}

三、Dijkstra算法的优化

先来看一道进阶版的习题。
Dijkstra算法的优化
这道题的话我们是不能用朴素Dijkstra算法做的，会TLE。

所以呢？
我们可以用堆来优化找没有确定最短距离的点那一步。
这里就不手动实现堆了，STL！

（附：以前没讲堆是因为那玩意太太太……恶心了………………学过的人都知道模拟堆的代码有多么的恶心。）

所以说，优先队列是个好东西！

priority_queue!!!!!!!!

好了不水了，下面正式开始优化。
第一步，定义，定义小根堆。

priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> heap;

每个数的第一个节点表示距离，第二个节点表示点的编号。
然后像朴素Dijkstra算法一样把第一个节点放进堆。

heap.push({0, 1});

接着就运行一遍标准板子。
代谢n遍变成一个类似宽搜的过程。

while(heap.size())
{
    auto t = q.top();
    q.pop();
}

这里取出堆顶，相当于在朴素Dijkstra算法中找到找到目前不在st中距离最近的点。
接着取出当前点的编号，放进vel。

int vel = t.second;

如果当前点已经确定最短距离了就把ta扔掉。

if(st[vel]) continue;

否则的话这个点就需要我们去计算最短路了。
计算最短路，总共分三步！

哪三步？
一标记，二遍历，三更新。

一标记

标记st数组就行了。
很弱。

st[vel] = true;

二遍历

使用邻接表遍历标准模板。

for(int i = h[vel]; i != -1; i = ne[i])
{
    int j = e[i];
}

三更新

如果当前这个点是可以的。

if(dist[j] > dist[vel] + w[i])

那我们就更新。
首先更新dist[j]。

dist[j] = dist[vel] + w[i];

然后更新优先队列heap。

heap.push({dist[j], j});

一切结束后我们看一下当前这个点有没有最短路即可。

if(dist[n] == 0x3f3f3f3f) return -1;
return dist[n];

我们称这种算法为堆优化Dijkstra算法。

完整の板子：

int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> heap;
    heap.push({0, 1});
    while(heap.size())
    {
        auto t = heap.top();
        heap.pop();
        int vel = t.second;
        if(st[vel]) continue;
        st[vel] = true;
        for(int i = h[vel]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > dist[vel] + w[i])
            {
                dist[j] = dist[vel] + w[i];
                heap.push({dist[j], j});
            }
        }
    }
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}

走你！

本题完整代码：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 1000010;
int n, m, h[N], w[N], e[N], ne[N], idx, dist[N];
bool st[N];
void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}
int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> heap;
    heap.push({0, 1});
    while(heap.size())
    {
        auto t = heap.top();
        heap.pop();
        int vel = t.second;
        if(st[vel]) continue;
        st[vel] = true;
        for(int i = h[vel]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(dist[j] > dist[vel] + w[i])
            {
                dist[j] = dist[vel] + w[i];
                heap.push({dist[j], j});
            }
        }
    }
    if(dist[n] == 0x3f3f3f3f) return -1;
    return dist[n];
}
int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for(int i = 0; i < m; i ++){
        int a, b,c;
        cin >> a >> b >>c;
        add(a, b, c);
    }
    cout << dijkstra() << endl;
    return 0;
}

好了本期分享到这里就告一段落了。

这是作业

这是我的全部分享

bye~

（日常凑整，350）