二分图一般都是无向图问题, 但是因为我们只需要依次枚举一个点集中的点来分配对象，所以往往我们在代码实现时, 存边只存单向边。

要看一个图是不是二分图(染色法: 对于网格图奇点和偶点, 染色是不同的, 我们只需要看边是否都只在两个点集之间的), 我们主要看图的边的两个顶点是否都能被归为两种不同性质的点集, 而边只能在两个点集之间.

注: 二分图不一定有匹配, 下图就是一个二分图但是其无匹配

染色法判断二分图

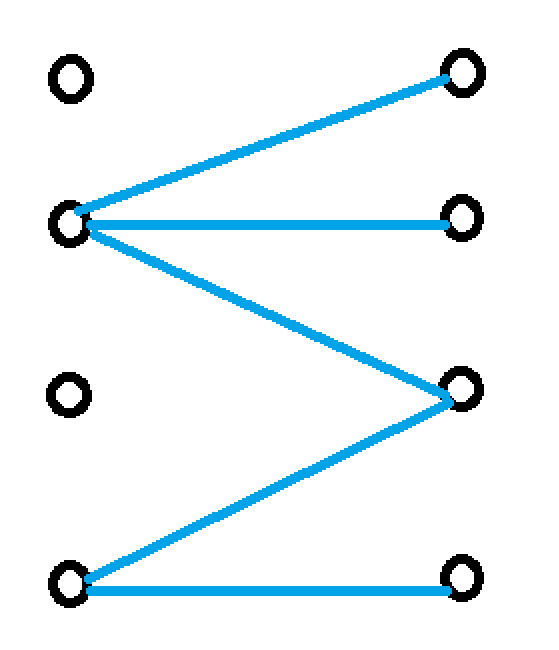
匈牙利算法(前提是图为二分图, 求的是二分图的最大匹配) – 模板见基础课打卡

该算法的vis数组的理解很重要 见基础课打卡代码详解
(两点之间有边, 能互通, 就有可能形成一组匹配)

注: 下面的概念非二分图特有, 图都有

匹配/匹配边: 与其他边没有公共节点的一条边, 我们称这条边为一个匹配/匹配边.
匹配点: 匹配边上的点
非匹配点: 不在匹配边上的点
非匹配边: 图中两点之间的边不是匹配边的边
最大匹配(匹配边数量的最大值): 最多连多少条边, 使得所有的边无公共点
增广路(径): 一边的非匹配点到另一边的非匹配点的一条非匹配边和匹配边交替经过的路径. (只要有一条增广路径就能多一组匹配, 最大匹配 $\Leftrightarrow$ 不存在增广路径)

最小点覆盖问题

定义: 给我们一个图(任意), 我们从中选出最少的点, 使得图中的每一条边至少有一个顶点被选.

二分图的最小点覆盖问题

二分图的最小点覆盖 = 二分图的最大匹配数
如下图, 最大匹配为3(3条匹配边), 最小点覆盖(3个点)

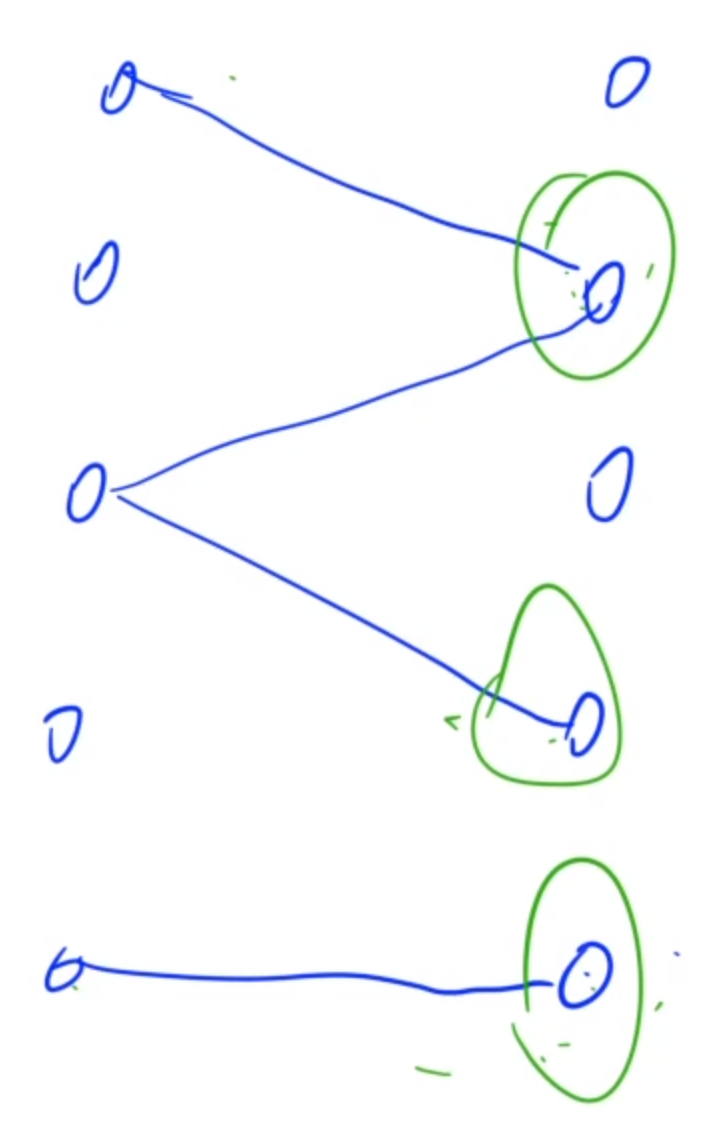
例题

最大独立集问题(NPH问题)

定义: 从图中选出最多的点, 使得选出的点集中任意两点之间没有边.

• 最大团

  原图的最大独立集就是补图(原图有的边去掉, 没的边加上)的最大团

二分图中的最大独立集问题

最大独立集 = 二分图的总点数 - 最大匹配
例题

最小路径点覆盖问题(最小路径覆盖问题)

分类:
1. 最小不相交路径覆盖: 对于一个有向图来说, 用最少的互不相交(路径无公共点)的路径, 遍历所有的点.
2. 最小可相交路径覆盖: 对于一个有向图来说, 用最少的路径, 遍历所有的点.

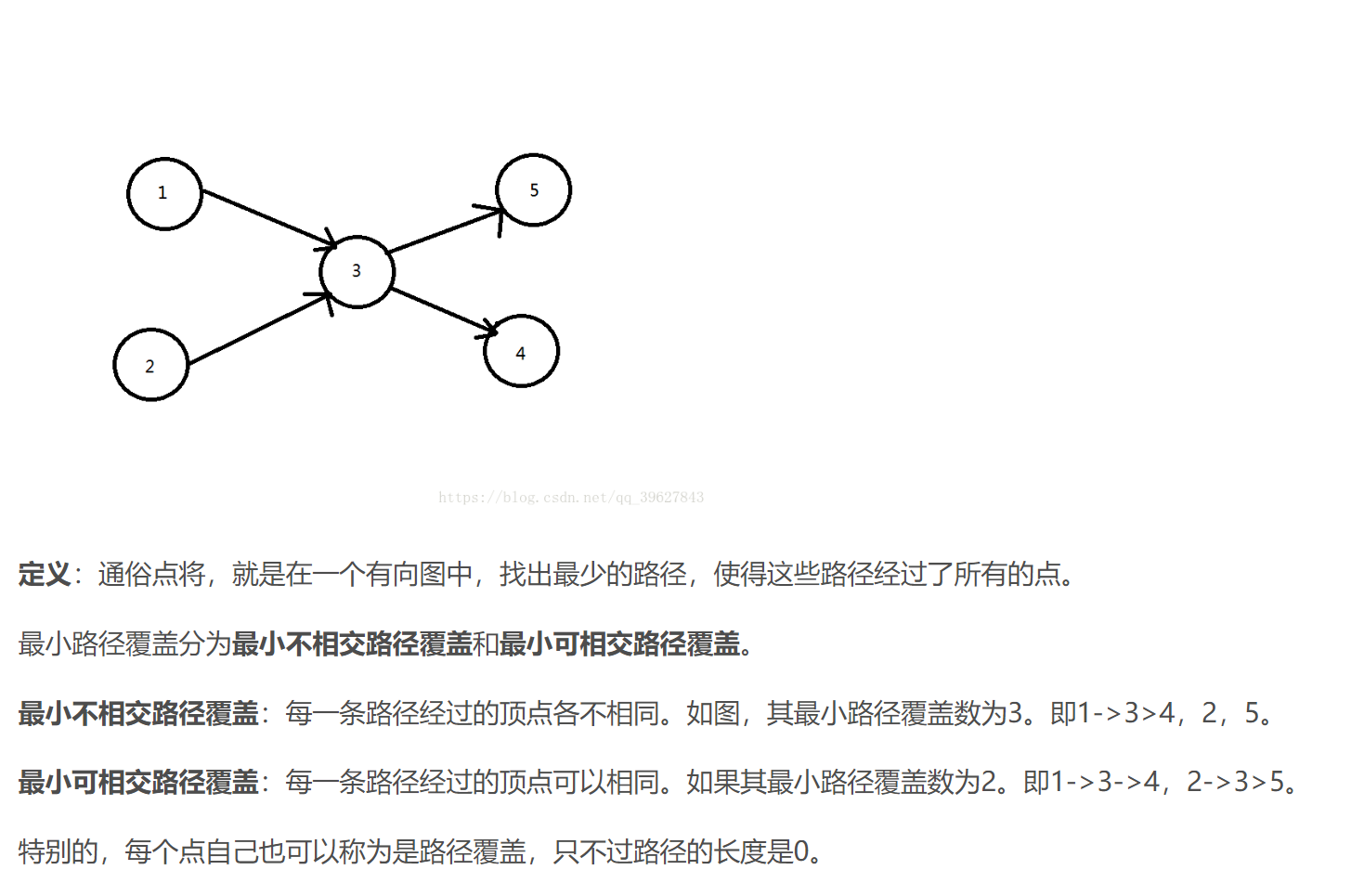
二分图算法求解最小不相交路径覆盖问题

• 拆点: 对于每个顶点, 我们建一个相对它的新点, 如图所示 (我们可以联想到, 那么我们求一般图的其他问题, 是否能将其拆点转化为二分图在求呢???)

  

然后我们将i -> j的一条边转化为i -> j’的一条边, 这样的话, 这个图必然是一个二分图(边都不在内部).
结论: 最少路径 = 点数(注意是原图的点数, 非二分图的点数) - 二分图的最大匹配.
证明:

二分图算法求解最小可相交路径覆盖问题

• 求原图的传递闭包
• 对传递闭包求一遍最小不相交路径覆盖 = 原图的最小可相交路径覆盖
  例题