前缀和

什么是前缀和？

• 前缀和可以简单理解成一个数组的前$n$项的和
• 前缀和也是一种重要的预处理手段

有一个数组$a[1], a[2], a[3], \cdots, a[n]$

令$sum[0]=0, sum[1]=a[1], sum[2]=a[1]+a[2]$

$sum[1]=a[1]+a[2]+\cdots+a[i]$，即$sum[i]$为$a[1] \sim a[i]$的和

$sum$数组我们即称为前缀和数组

任何一段数组的和都可以表示成两个前缀的差

$sum[i-1]=a[1]+a[2]+a[3]+\cdots+a[i-1]$

$sum[j]=a[1]+a[2]+a[3]+a[4]+\cdots+a[i-1]+a[i]+a[i+1]+\cdots+a[j]$

$sum[j]-sum[i-1]=a[i]+a[i+1]+a[i+2]+a[i+3]+\cdots+a[j]$

即数组中$a[i] \sim a[j]$的和，我们可以用$sum[j]-sum[i-1]$来表示

二维前缀和

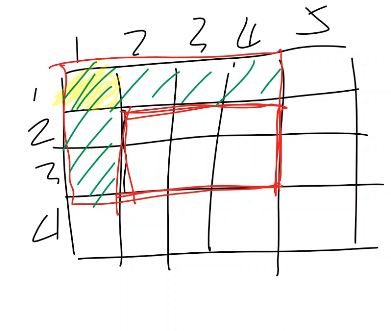
给出$m \times n$的二维矩阵

询问$(x_1, y_1) \sim (x_2, y_2)$的子矩阵和

$sum[x][y]$表示$(1, 1) \sim (x, y)$这个子矩阵的和

$sum[x][y]=a[x][y]+sum[x-1][y]+sum[x][y-1]-sum[x-1][y-1]$

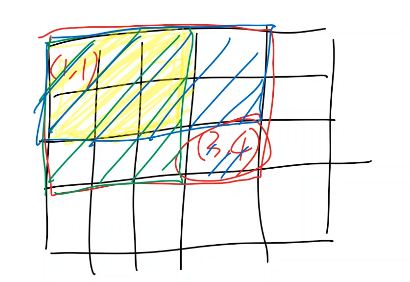
询问$(x_1, y_1) \sim (x_2, y_2)$的子矩阵和
$=sum[x_2][y_2]-sum[x_2][y_1 - 1]-sum[x_1-1][y_2]+sum[x_1-1][y_1-1]$

素数

什么素数（质数）

定义：除了$1$与它本身以外不再有其他因数。

素数判断

对于一个整数$n$，我们有如下几种方法判断其是否是一个素数。

算法一：枚举$2 \sim n-1$，如果都除不尽，证明这个数是素数。时间复杂度为$O(n)$。

算法二：对于一个小于$n$的整数$x$，如果$n$不能整除$x$，则$n$必定不能整除$n/x$，就是只要从$2$枚举到$\sqrt{n}$即可。时间复杂度为$O(\sqrt{n})$。

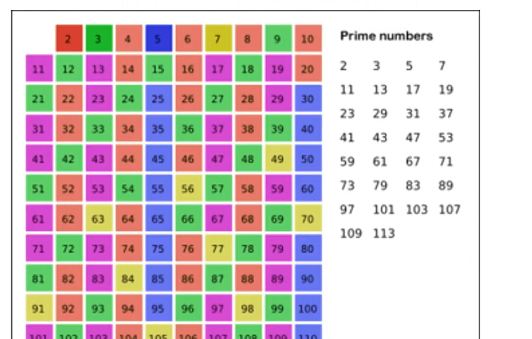
素数筛法

求$2 \sim n$内的所有素数： 素数个数

使用普通筛法（也就是没那么快）

假设全部都是素数，当找到一个素数时，显然这个素数乘上另外一个数之后都是合数
把这些合数都筛掉（去掉）

代码实现

void make_prime(int n) {
    memset(prime, 1, sizeof(prime));
    prime[0] = false;
    prime[1] = false;
    for (int i = 2; i <= n; ++i) {
        if (prime[i]) {
            cnt++;
            for (int k = i * i; k <= n; k += i) 
                prime[k] = false;
        }
    }
}


\\ 版本二：
void sieve(int n) {
    memset(isPrime, true, sizeof(isPrime));
    for (int i = 2; i * i <= n; ++i) {
        if (isPrime[i])
            for (int j = i * i; j <= n; j += i) isPrime[j] = false;
    }
}

线性素数筛法（欧拉筛法）

编程求$2 \sim n$（$n$ 为大于$2$的正整数）中有多少个素数。 注意$n$很大
素数个数 进阶版

“一般”筛法（也就是没那么快），还是不那么高效，即一个合数有可能被筛多次，比如$105$，即会被$3$筛一次，还会被$5$筛一次，也还会被$7$筛一次。

在”一般”筛法的基础上，我们能否提高效率，只需要保证每一个合数，只会被一个素因数筛掉即可。

进一步思考：

每一个合数，如果只会被最小的那个素因数筛掉，那么这个筛法的复杂度就是线性的。

比如$18$不是素数，$18 = 2 * 9 = 3 * 6$

最小的素数$* i$去删掉一个这个数

$6$里面含有$2$，所以不存在$3 * 6$去筛掉$18$，$3 * 6 = 3 * 2 * 3$

因此也不存在$5 * 6$去筛掉$30$，$5 * 6 = 5 * 2 * 3 = 30$，因此$30$可以通过$2 * 15$筛掉。

代码实现：

long prime[N] = {0}, num_prime = 0;
int isNotPrime[N] = {1, 1};
int main() {
    for (long i = 2; i < N; ++i) {
        if (!isNotPrime[i]) 
            prime[num_prime++] = i;
        for (long j = 0; j < num_prime && i * prime[j] < N; ++j) {
            isNotPrime[i * prime[j]] = 1;
            if (!(i % prime[j])) break;
        }
    }
    return 0;
}


\\ 版本二：
void Euler_sieve(int n) {
    memset(isPrime, true, sizeof(isPrime));
    for (int i = 2; i <= n; ++i) {
        if (isPrime[i]) prime[++prime[0]] = i; // 把素数保存到素数表prime中
        for (int j = 1; j <= prime[0] && i * prime[j] <= n; ++j) {
            isPrime[i * prime[j]] = false; // 筛除i*prime[j] 
            if (i % prime[j] == 0) break;
        } 
    }
}

• 欧拉筛法可以用来计算欧拉函数、莫比乌斯函数等积性函数。

一些练习题：

1、 最大子段和
2、 求和
3、 地毯
4、 海底高铁
5、 最大加权矩形
6、 领地选择
7、 光骓者的荣耀
8、 线性筛素数
9、 Not Divisible
10、连续自然数和