复习看啊哈算法(y总这一节讲的很bad不建议看)

分类

• 边强连通分量 e-dcc
• 点强连通分量 v-dcc

边双连通分量

• 桥(割边)

  对于一个无向连通图来说, 如果我们删除一条边之后, 图变得不再连通了, 那么我们九讲这条边称为桥.

• 定义

  一个极大的(图中不存在任何一个非连通块中的点加入连通块之后, 该连通块依然是连通块)不包含桥的连通块

• 性质

  1. 对于一个边连通分量来说, 我们不管删除连通分量的哪一条边, 它都是连通的.
  2. 对于一个边连通分量来说, 任意两点之间至少包含两条不相交的路径(两条路径上无公共边) 这是一个充要条件

• tarjan算法求边双连通分量

  1. 无向图不存在横叉边
     因为双向不存在后面能到前面, 前面不能到后面的情况, 那么如果存在后面连到前面的一条边, 那么dfs序遍历的时候, 我们就已经将后面的点遍历到了, 就不可能再后面再遍历到后面那个点了.
  2. 时间戳
     dfn[u]: 遍历到当前节点的编号
     low[u]: 不经过走过来的那条边(父边)能走到的最小编号节点
  3. 判断桥
     对于x, y之间的一条边, 如果low[y]能到x的祖先节点, 那么就不是桥, 若low[y] = y, 即是桥
     $dfn[x] < low[y] (严格小于)$

找e-dcc代码思路:
1. 将所有的桥删掉剩下的都是边连通分量了
2. 用栈存储搜到的所有点, 当搜到一个点的dfn[x] == low[x], 即这个点上面的一条边就为桥, 将栈中所有点标记即可
找e-dcc代码模板:

void tarjan (int u, int f) // f是u这个点由哪条边过来的, 哪条边的序号
{
    dfn[u] = low[u] = ++ timestamp;
    st[++ tt] = u;

    for(int i = h[u] ; ~i ; i = ne[i])
    {
        int j = e[i];
        if(!dfn[j])
        {
            tarjan(j, i);
            low[u] = min(low[u], low[j]);
            if(dfn[u] < low[j]) // 等于也不是桥
                is_bridge[i] = is_bridge[i ^ 1] = 1; // 蓝书位运算的操作
        }
        else if(i != f ^ 1) // 不经过父边 必定不是桥 是边连通分量, 无需判重数组
            low[u] = min(low[u], dfn[j]);
    }

    if(dfn[u] == low[u]) // 第一个非边双连通分量中的点是入了栈的
    {
        int y;
        dcc_cnt ++ ;

        do
        {
            y = st[tt -- ];
            id[y] = dcc_cnt;
        }while(y != u);
    }
}

性质2例题 将一棵树变成一个边双连通分量最少加边数

点双连通分量

• 割点 每一个割点都至少属于两个连通分量

  对于一个无向连通图来说, 如果我们删除某个点之后, 该连通图不连通了, 那么我们就称其为该联通图的割点.

• 定义

  一个极大的不包含割点的连通块

• tarjan算法求点双连通分量

  1. 时间戳
     dfn[u]: 意义同边双连通分量
     low[u]: 每个顶点在不经过父节点的情况下能到的最小编号顶点, 如果low[u]大于等于dfn[father] (就是不能到已经遍历过的点, 即father的祖先节点), father为割点.
  2. 判断(找)割点
     见啊哈算法讲的真的好 + 代码模板.
     例题 将一个无向图删去一个点能得到的连通块数量的最大值

找v-dcc代码模板

// cc_cnt: 连通分量的数量, 而非点双
void tarjan(int u) // 找割点和所有连通分量(找子连通分量, 这种找法补不重不漏)
{
    dfn[u] = low[u] = ++ timestamp;
    stk[ ++ top] = u;

    if (u == root && h[u] == -1) // 无边节点, 单点v-dcc
    {
        cc_cnt ++ ;
        cc[cc_cnt].push_back(u);
        return;
    }

    int cnt = 0;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (!dfn[j])
        {
            tarjan(j);
            low[u] = min(low[u], low[j]);
            if (dfn[u] <= low[j]) // 对于根节点来说, 这个是必然满足的  把所有以u为根节点的子连通块全部存下来  不能不通过这个点到u的祖先节点, 则u就是这个连通分量的割点
            {
                cnt ++ ; // 儿子数量
                if (u != root || cnt > 1) cut[u] = true; // 1. 不是根节点, 2. 是根节点, 要有两个儿子才是割点
                ++ cc_cnt; // 我们待会儿通过连通块中割点的个数判断点双连通分量
                int y;
                do 
                {
                    y = stk[top -- ];
                    cc[cc_cnt].push_back(y);
                } while (y != j); // 如果写成y != u, 由于一个点可能属于多个v-dcc, 则u被第一个cc弹出之后, 后面的cc就永远没有u这个点了就会死循环. (后面单独加上)
                cc[cc_cnt].push_back(u); // u点也是该cc的一部分
            }
        }
        else low[u] = min(low[u], dfn[j]); // 无需vis判重数组的原因: 由于在有向图的强连通分量中, u能走到的点, 不一定是属于该SCC(因为该点不一定就能到u), 只有在栈中的才属于, 而无向图能走到的点就一定属于当前连通块
    }
}

void find ()
{
    for (int i = 1; i <= cc_cnt; i ++ )
    {
        int cnt = 0;
        for (int j = 0; j < cc[i].size(); j ++ )
            if (cut[cc[i][j]]) // 割点数组
                cnt ++ ;

        if (cnt == 0) // 割点为0就是v-dcc
        {
            cout << i << endl;
        }
        else puts("No V-dcc");
    }
}

例题

注意:

• 两个割点之间的边不一定是桥
  
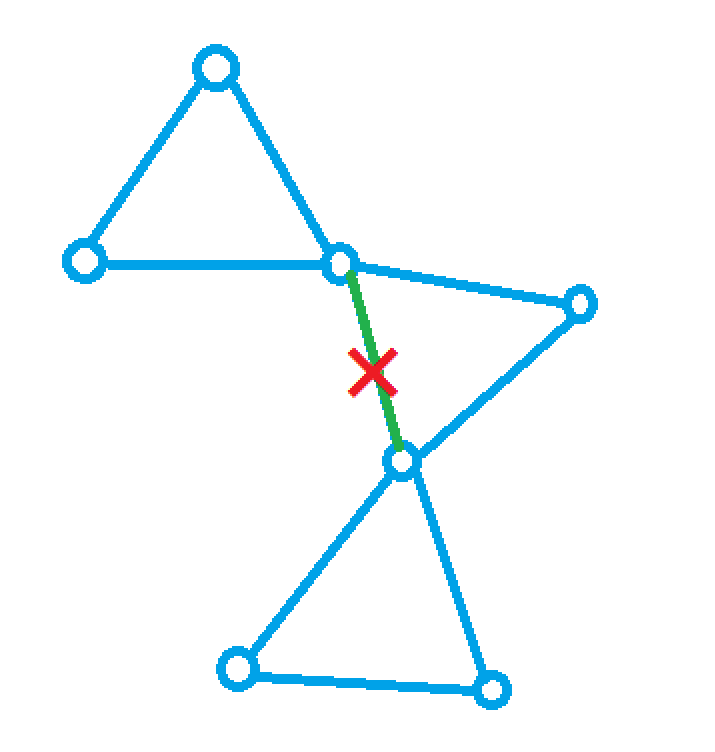
• 一个桥的两个端点也不一定是割点
  ⚪-⚪这样的图显然中间的边是桥, 但是这两个点任删一个点图依然连通, 所以该点非割点.
• 点连通分量不一定是边连通分量, 反之也不一定.