圆方树
前言
前置知识: tarjan 无向图强连通分量
仙人掌图定义
任意一条边至多只出现在一条简单回路的无向连通图称为仙人掌。
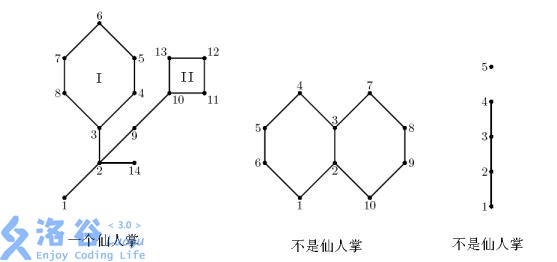
圆方树定义及构建
圆方树是将仙人掌图转化为树的形态。
其中有圆点和方点,圆点表示原图的点。
每一个方点表示仙人掌的一个简单回路。
对于每一个简单回路,
选一个点作为根,并向对应方点连权值为 0 的边。
再从方点连向其余节点,权值为根到该点的最短距离(顺时针或逆时针)。
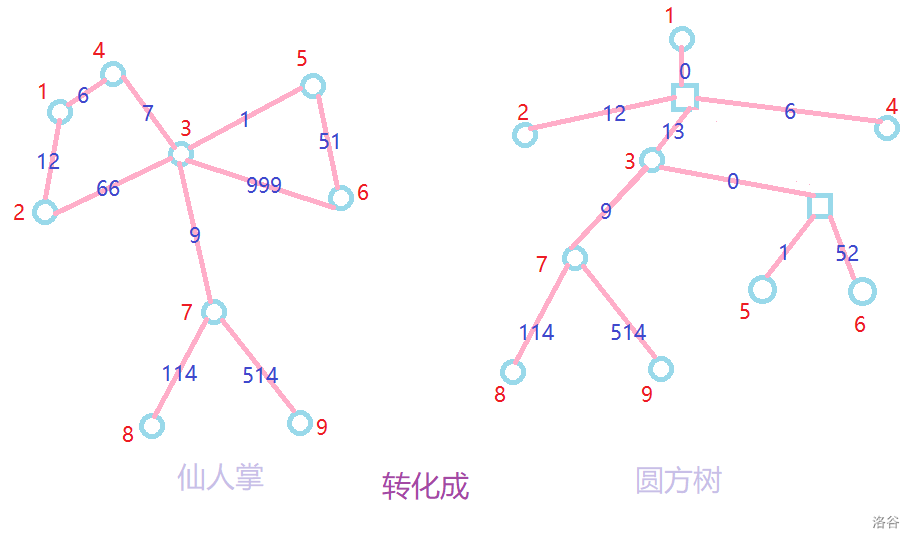
其中的环可用 tarjan算法 求强连通分量找出。
实现
void build_circle(int x, int y, int z)
{
int sum = z;
for (int k = y; k != x; k = fu[k])
{
s[k] = sum;
sum += fw[k];
}
s[x] = stot[x] = sum;
add(h2, x, ++ new_n, 0);
for (int k = y; k != x; k = fu[k])
{
stot[k] = sum;
add(h2, new_n, k, min(s[k], sum - s[k]));
}
}
void tarjan(int u, int from)
{
dfn[u] = low[u] = ++ times;
for (int i = h1[u]; ~i; i = ne[i])
{
int j = e[i];
if (!dfn[j])
{
fu[j] = u, fw[j] = w[i], fe[j] = i;
tarjan(j, i);
low[u] = min(low[u], low[j]);
if (dfn[u] < low[j]) add(h2, u, j, w[i]);
}
else if (i != (from ^ 1)) low[u] = min(low[u], dfn[j]);
}
for (int i = h1[u]; ~i; i = ne[i])
{
int j = e[i];
if (dfn[u] < dfn[j] && fe[j] != i)
build_circle(u, j, w[i]);
}
}
广义圆方树
广义圆方树相当于在圆方树的基础上,将相邻的两个圆点看作一个双连通,在他们之间加入一个方点。
广义圆方树比圆方树更加实用,因为它拥有更好的性质:每条边连接一个原点和一个方点。
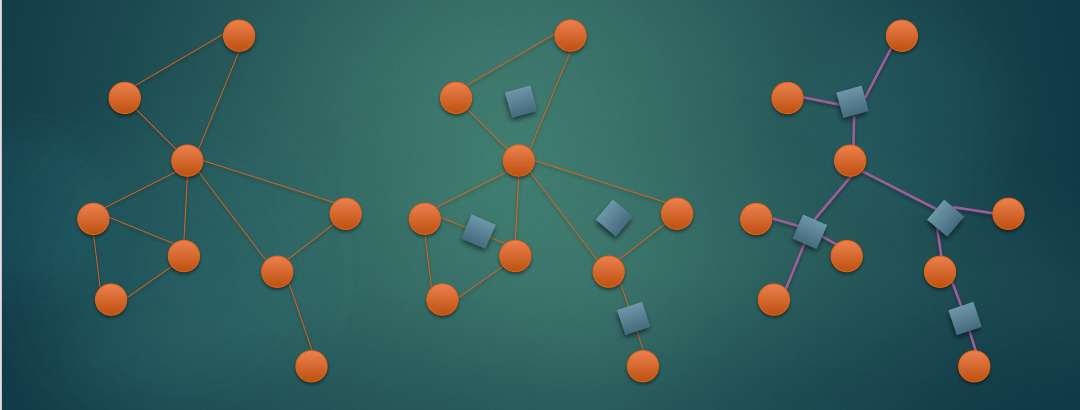
实现
void tarjan(int u, int fa) {
dfn[u] = low[u] = ++ top;
for (int i = h[u]; ~i; i = ne[i]) {
int ver = e[i];
if (ver == fa) continue;
if (!dfn[ver]) {
stk[++ tt] = i;
tarjan(ver, u);
low[u] = min(low[u], low[ver]);
if (low[ver] >= dfn[u]) {
add(h2, ++ scc_cnt, u), add(h2, u, scc_cnt);
do {
add(h2, scc_cnt, e[stk[tt]]), add(h2, e[stk[tt]], scc_cnt);
} while (stk[tt -- ] != i);
}
} else low[u] = min(low[u], dfn[ver]);
}
}


update at 10.25 : 更新广义圆方树