题目描述

给定一个模式串S，以及一个模板串P，所有字符串中只包含大小写英文字母以及阿拉伯数字。

模板串P在模式串S中多次作为子串出现。

求出模板串P在模式串S中所有出现的位置的起始下标。

输入格式

第一行输入整数N，表示字符串P的长度。

第二行输入字符串P。

第三行输入整数M，表示字符串S的长度。

第四行输入字符串M。

输出格式

共一行，输出所有出现位置的起始下标（下标从0开始计数），整数之间用空格隔开。

数据范围

1≤N≤104
1≤M≤105
输入样例：
3
aba
5
ababa

输出样例：

0 2

思路：

暴力算法该怎么做

for(int i=1;i<=n;i++) //枚举当前起点，看是否成功
{
    bool flag = true;
    for(int j=1;j<=m;j++)
        if(s[i] != p[j])
        {
            flag = false;
            break;
        }
}

如何去优化

对于模板串数组需要做预处理
首先讲一下字符串前缀和后缀的定义，如果字符串A和B，存在A=BS，其中S是任意的空字符串，那么B为A的前缀，同样可以定义后缀。比如abc的前缀包括{a,ab}，后缀包括{c,bc}。
PMT表中的值表示字符串的前缀集合与后缀集合的交集中最长元素的长度，例如，对于aba,它的前缀集合是{a,ba}，后缀集合是{ba,a}那么它在PMT表中的值就是1。
要在主字符串ababababca中查找模式字符串abababca。如果在j处字符不匹配，那么由模式字符串PMT的性质，主字符串中i指针之前的PMT[j-1]位就一定与模式字符串的第0位至第PMT[j-1]位是相同的。因为主字符串在i位失配，也就意味着主字符串从i-j到i这一段是与模式字符串0到j这一段是完全相同的。
以图中例子来说，在i处失配，那么主字符串和模式字符串的前6位就是相同的。又因为模式字符串的前6位的前4位后缀和前缀是相同的，所以可以推出主字符串i之前的4位和模式字符串开头的4位是相同的，就是图中灰色部分，那么这部分就不用再比较了。

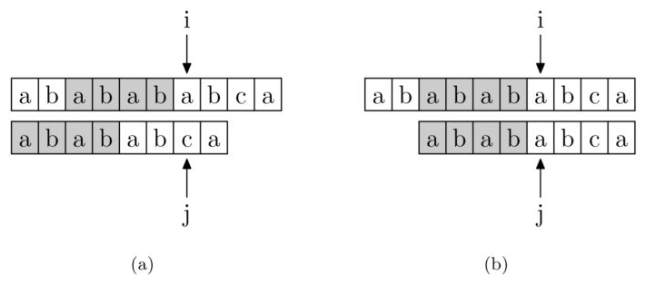
由于在j位失配，影响j指针回溯的位置其实是第j-1位的PMT值，所以为了编程的方便，我们不直接使用PMT数组，而是将PMT数组后移一位，将新的数组称为next数组。如下图所示

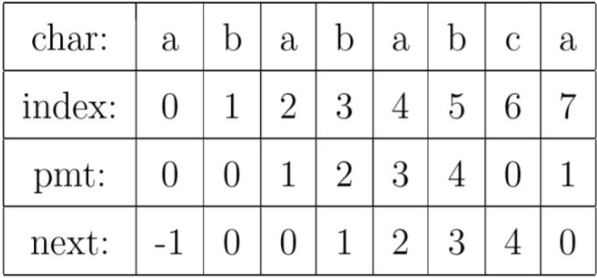
编程快速求解next数组的过程就是从模式字符串的第1位（下标从0开始）开始对自身进行匹配运算，在任一位置，能匹配到的最长长度就是当前位置的next值。

具体实现如下：

#include<iostream>

using namespace std;

const int N = 10010,M = 100010;

int n,m;
char p[N],s[M];
int ne[N];

int main()
{
    cin >> n >> p+1 >> m >> s+1;

    //求next的过程
    for(int i=2,j=0;i<=n;i++)
    {
        while(j && p[i] != p[j+1]) j = ne[j];
        if(p[i] == p[j+1]) j++;
        ne[i] = j;
    }

    // kmp匹配过程
    for(int i=1,j=0;i<=m;i++)
    {
        while(j && s[i] != p[j+1]) j = ne[j]; //如果不能j往前走，就退一步
        if(s[i] == p[j+1]) j++;
        if(j == n)
        {
            // 匹配成功
            printf("%d ",i-n);
            j = ne[j]; 
        }
    }

    return 0;
}