应该不会有人跑去写斐波那契堆的吧？

Latex 已炸，建议 Goto 原网址： https://xjx885.coding-pages.com/post/u3KjOvd_5/

[HTML_REMOVED]

前言：

$~\\$

$\quad\quad$ 日常做笔记。

$~\\$

正文：

$\quad\quad$ 配对堆是可并堆的一种，支持快速插入元素，合并两个堆，删除堆顶元素，更改堆顶元素的值，但在 OI 界较为冷门。

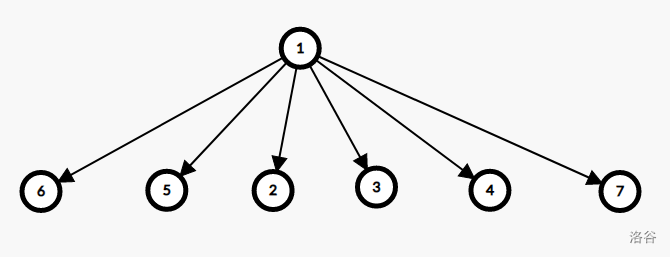
$\quad\quad$ 存储：其本质上是一颗树的结构，但存储时只存储某个节点的左儿子与右兄弟。

$\quad\quad$ 就像下面这两幅图：前者是一棵树，后者是配对堆，后者本质上就是前者，但二者存储方式不同。

$~\\$

$~\\$

$\quad\quad$ 合并：其合并操作非常简单，如果是小根堆，就把根大的堆往根小的堆上面贴就好了，反之亦然。

$\quad\quad$ 代码（$a,b$ 是待合并的两个堆的根节点，返回值为合并后的根）：

int merge(int a, int b)
{
    if(!a || !b || a == b) return a ? a : b;
    //如果该操作有意义
    if(d[a] < d[b]) swap(a, b);
    //强制让a往b上贴

    point[a].xd = point[b].son , point[b].son = a;
    return b;
}

$\quad\quad$ 插入：插入节点的话，把新节点作为一个单独的堆 $\operatorname{merge}$ 进来就好了，合并和插入的复杂度显然是 $O(1)$。

$~\\$

$~\\$

$\quad\quad$ 修改：配对堆的修改分两种情况（以小根堆为例），第一种是把某一个值改大（一般不用），第二种是把某一个值改小。

$\quad\quad$ 第一种操作会破坏该节点的子树结构，所以没办法高效的完成，只能把以该节点为根的子树剖出来，然后删去它的最小值（该节点），插入该节点修改后的值，最后与原堆合并。复杂度与删去节点（该操作在下面）的复杂度相同（$O(logn)$）。

$\quad\quad$ 第二种操作不会破坏该节点的子树结构，可以直接剖出以该节点为根的子树，修改该节点的值，然后与原堆合并即可，复杂度显然是 $O(1)$，但因为会破坏原有势能分析过程，导致其均摊复杂度不好计算。

$\quad\quad$ 这里就不放代码了，这操作不咋常用。

$~\\$

$~\\$

$\quad\quad$ 删除：删除是配对堆最麻烦的操作，一个朴素的想法是：删除堆顶节点时，把堆顶节点的儿子从左往右一个个 $\operatorname {merge}$ 到一起，形成一个新的堆，然后把原来的堆顶节点丢掉就好。如果删除的不是堆顶节点，把它剖出来再操作即可。

$\quad\quad$ 这样做复杂度显然是 $O(n)$ 的，承受不起。

$\quad\quad$ 降低复杂度的一个很好方法是 “配对”，即从左往右把根的儿子两两合并成二元组，然后从右往左把这些二元组依次合并。

$\quad\quad$ 如下图，删除之前用树形结构表示，删除过程（P2~P4）用存储结构（左儿子右兄弟）表示：

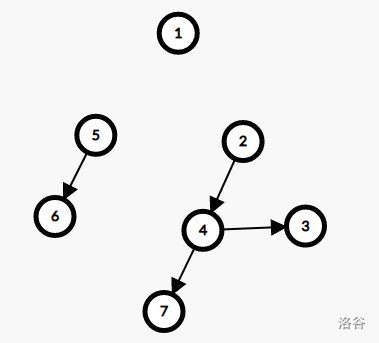
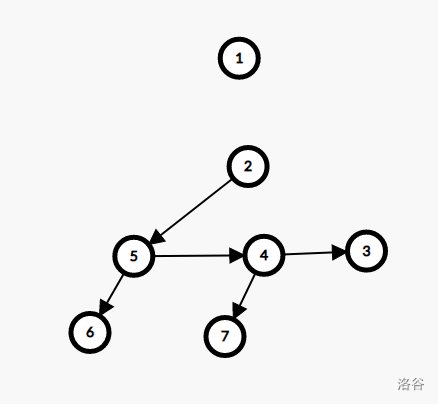
$\quad\quad$ 显然，这里任然 $\operatorname{merge}$ 了 $n-1$ 次，但是其均摊复杂度是 $O(logn)$ 的，具体证明可以去翻配对堆论文。

$\quad\quad$ 代码：

$\quad\quad$ 递归合并部分：

int merges(int x)
{
    if(!x) return 0;
    if(!xd[x]) return x;

    int a = xd[x], b = xd[a];
    return merge(merge(x, a), merges(b));
}

$\quad\quad$ 调用删除节点 $a$ 时直接 merge(son[a]) 就行了。

$~\\$

$~\\$

$\quad\quad$ 例题：P3377 【模板】左偏树（可并堆）。

$\quad\quad$ 本题中，给出要求合并的点并不一定是根节点，所以要用并查集维护每个点所在堆的根节点。

$\quad\quad$ 注意：配对堆用带路径压缩的并查集维护根节点是谁时，在删去某个节点后，需要把该节点的 $fa$ 指向新建出的堆的根节点，否则并查集的查询链会断掉。

$\quad\quad$ 代码：

#include <bits/stdc++.h>

using namespace std;

const int N = 100010;

inline int read()
{
    int x = 0, ch = '~', fh = 1;

    while(!isdigit(ch)) fh = ch == '-' ? -1 : 1, ch = getchar();
    while(isdigit(ch)) x = (x << 3) + (x << 1), x += ch - '0', ch = getchar();

    return x * fh;
}

int n, m, d[N], fa[N], del[N];

struct node
{
    int son, xd;
} point[N];

int merge(int a, int b)
{
    if(!a || !b || a == b) return (!a) ? b : a;
    if(d[a] < d[b] || d[a] == d[b] && a < b) swap(a, b);

    point[a].xd = point[b].son , point[b].son = a;
    return fa[a] = b;
}

int merges(int x)
{
    if(!x ) return 0;
    fa[x] = x;
    if(!point[x].xd) return x;

    int a = point[x].xd, b = point[a].xd;
    fa[a] = a, point[x].xd = point[a].xd = 0;
    return merge(merge(x, a), merges(b));
}

int find(int x)
{
    return x == fa[x] ? x : fa[x] = find(fa[x]);
}

int main()
{
    n = read(), m = read();
    for(register int k = 1; k <= n; k++)
        d[k] = read(), fa[k] = k;

    for(register int k = 1; k <= m; k++)
    {
        int opt = read(), x = read(), y;
        if(opt == 1) y = read();

        if(opt == 1)
        {
            if(!del[x] && !del[y])
                merge(find(x), find(y));
        }

        else if(!del[x])
        {
            int top = find(x);

            printf("%d\n", d[top]), del[top] = 1;
            fa[top] = merges(point[top].son);
        }
        else
            printf("-1\n");
    }

    return 0;
}

$~\\$

$~\\$

$\quad\quad$ 树上操作例题：P1552 [APIO2012]派遣。

$\quad\quad$ 其实是差不多的，把序列上的操作放在树上， $dfs$ 分别处理就好。

$\quad\quad$ 代码：

#include <bits/stdc++.h>
#define int long long

using namespace std;

const int N = 1000010;

inline int read()
{
    int x = 0, ch = '~';

    while(!isdigit(ch)) ch = getchar();
    while(isdigit(ch)) x = (x << 3) + (x << 1), x += ch - '0', ch = getchar();

    return x;
}

int n, m, C[N], add[N], size[N], L[N], fa[N], lson[N], rxd[N];
vector <int > son[N];

int find(int x)
{
    return x == fa[x] ? x : fa[x] = find(fa[x]);
}

int merge(int u, int v)
{
    if(!u || !v || u == v) return u ? u : v;
    if(C[u] > C[v]) swap(u, v);

    rxd[u] = lson[v], lson[v] = u, add[v] += add[u], size[v] += size[u];
    return fa[u] = v;
}

int merges(int x)
{
    if(!x) return 0;
    if(!rxd[x]) return x;

    int a = rxd[x], b = rxd[a];
    return merge(merge(x, a), merges(b));
}

int pop(int x)
{
    fa[x] = merges(lson[x]);
    return fa[x];
}

int answ;

void dfs(int root)
{
    int now = find(root);
    answ = max(answ, size[now] * L[root]);
    for(register int k = 0; k < (int )son[root].size(); k++)
    {
        int to = son[root][k];
        dfs(to), now = merge(find(now), find(to));
        while(add[now] > m) now = pop(now);
        answ = max(answ, size[now] * L[root]);
    }
}

signed main()
{
    n = read(), m = read();
    for(register int k = 1; k <= n; k++)
    {
        int v = read();
        if(v) son[v].push_back(k);
        add[k] = C[k] = read(), L[k] = read(), fa[k] = k, size[k] = 1;
    }

    dfs(1);

    printf("%lld",answ);

    return 0;
}

结语：

$\quad\quad$ 话说会有人闲的没事干在比赛中写斐波那契堆的吗？

$$\large\color {#123456} {E \ N \ D}$$