前置知识：AC自动机

$后缀自动机(\mathcal{SAM})$

$引入$

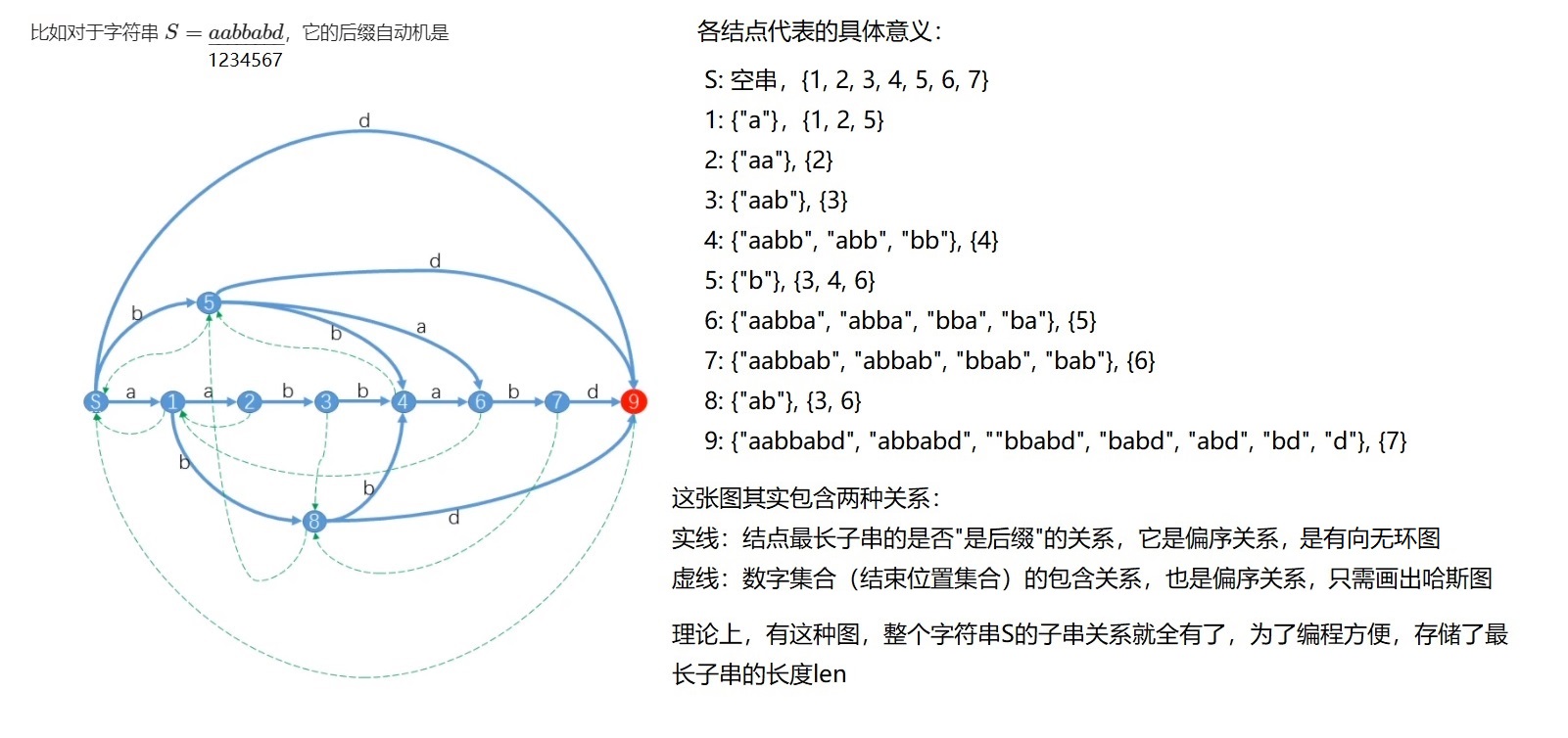
给你一个字符串，要求给出一个点数，边数线性的自动机，满足这个自动机能表示出 $s$ 的所有子串。

一个想法是将 $s$ 的所有后缀取出，然后加入一个 $AC$ 自动机中，这样显然行不通，但是如果将某些性质相同的点看作同一个点，那么就可能建出要求的自动机。

$定义$

如图，有 $1$ 个起点 $S$，每 $1$ 条边代表$1$个字符，从 $S$ 出发的所有路径(指蓝边)都对应了原串的 $1$ 个子串

所有蓝边构成$1$个有向无环图(拓扑图)，所有绿边构成$1$棵树

$性质$

定义节点$i$对应的字符串为自动机中从节点$S$出发到$i$的最长路径

$endpos(i)$ 表示为节点$i$对应字符串在原串中匹配成功时的所有末尾下标集合

当 $endpos(i)=endpos(j)$ 时，我们称 $i,j$ 属于同一等价类。

则有以下性质：

1. 令 $s1$，$s2$ 为 $S$ 的两个子串 ，不妨设 $|s1| \leq |s2|$ （我们用$|s|$表示 $s$ 的长度 ，此处等价于$s1$ 不长于$s2$）。则$s1$ 是 $s2$ 的后缀当且仅当 $endpos(s1)⊇endpos(s2)$ ，$s1$ 不是 $s2$ 的后缀当且仅当 $endpos(s1)∩ endpos(s2)=∅$　。

2. 两个不同子串的$endpos$，要么有包含关系，要么没有交集。

3. 两个子串的$endpos$相同，那么短串为长串的后缀。

4. 对于一个等价类 ，已知两个子串 $i,j$ 属于这个等价类且 $|i| < |t| < |j|$，其中 $t$ 为 $j$ 的某个后缀，那么 $t$ 也一定属于这个等价类。

5. 对于一个等价类，它包含的所有串的一定是最长串的一段连续后缀，例如最长串为 $\texttt{ciallo}$，那么这个等价类可以为 $\{ ciallo, iallo, allo \}$。

$后缀 \mathfrak{Link}$

对于一个等价类 $v$，设 $w$ 表示其中的最短串，则 $v$ 的后缀 $link$ 指向 $w$ 的长度为 $|w| - 1$ 的后缀 所在的等价类。

$构造$

点的定义：属于同一等价类的子串集被称为一个点。

边的定义：枚举所有非空子串 $b$，设 $a$ 为 $b$ 去掉末尾字符 $c$ 的字符串，则连一条边从 $a$ 所在的等价类到 $b$ 所在的等价类，边权 $c$，忽略重边和自环。

采用数学归纳法，我们假设我们已经拥有一个前 $n-1$ 个字符组成字符串 $a$ 的 $sam$，现在新加入一个字符 $c$，观察 $sam$ 发生的改变。

对于边来说，我们只对所有以下标 $n-1$ 结尾的子串加边到一个新节点 $c$，也就是只更新串 $a$ 所在的等价类 $v$，$link(v)$，$link(link(v))$ 等等。

对于点来说，可能某些串 $a$ 和串 $b$ 原本属于同一等价类，但加入 $c$ 后，$a$ 多了一个 $endpos$ 为 $n$，于是 $a,b$ 分裂。

那么 $a$ 一定是 $v, link(v), link(link(v)),…$ 中某个向权值为 $c$ 的边走的点。

具体如何构造就看代码，注意：

对于节点$i$，有$len$，$fa$，$ch[]$，

$len$ 表示为从节点$S$出发到$i$的最长路径长度，

$fa$ 表示为$endpos$包含$i$，且$endpos$与$i$最接近的点，即绿边，

$ch[]$ 表示为从$i$出发的边，即蓝边。

void extend(int c)
{
    int p = last, np = last = ++ tot;
    node[np].len = node[p].len + 1;
    for (; p && !node[p].ch[c]; p = node[p].fa) node[p].ch[c] = np; // 加边
    if (!p) node[np].fa = 1;
    else
    {
        int q = node[p].ch[c];
        if (node[q].len == node[p].len + 1) node[np].fa = q;
        else
        {
            int nq = ++ tot; // 开始分裂
            node[nq] = node[q], node[nq].len = node[p].len + 1;
            node[q].fa = node[np].fa = nq;
            for (; p && node[p].ch[c] == q; p = node[p].fa) node[p].ch[c] = nq;
        }
    }
}

$广义后缀自动机$

$定义$

对于多个串建广义自动机，自动机内包含每个串的子串。

$构造$

最容易想到的是将小串合并为大串，$S=S_1+$#$+S_2+$$$+S_3+\cdots$，坏处是没有那么多特殊字符，强行使用需要加特判，所以不常使用。

将所有串建一个 $trie$ 树，然后 $bfs$ 整棵树（注意 $dfs$ 是假的），每次加入时 $last$ 设置为父节点的 $np$。

$代码$

#include <bits/stdc++.h>
using namespace std;

const int N = 2000010;
int tot0 = 1, tot1 = 1;
int trie[N][26], pos[N];
struct Node {
    int ch[26], len, fa;
} node[N];

void ins(string t) {
    int p = 1;
    for (int i = 0; i < t.size(); i ++ ) {
        int c = t[i] - 'a';
        if (!trie[p][c]) trie[p][c] = ++ tot0;
        p = trie[p][c];
    }
}

int extend(int c, int lst) {
    int p = lst, np = lst = ++ tot1;
    node[np].len = node[p].len + 1;
    for (; p && !node[p].ch[c]; p = node[p].fa) node[p].ch[c] = np;
    if (!p) node[np].fa = 1;
    else {
        int q = node[p].ch[c];
        if (node[q].len == node[p].len + 1) node[np].fa = q;
        else {
            int nq = ++ tot1;
            node[nq] = node[q], node[nq].len = node[p].len + 1;
            node[q].fa = node[np].fa = nq;
            for (; p && node[p].ch[c] == q; p = node[p].fa) node[p].ch[c] = nq;
        }
    }
    return np;
}

void build() {
    queue<int> Q;
    pos[1] = 1;
    for (int i = 0; i < 26; i ++ )
        if (trie[1][i])
            Q.push(trie[1][i]), pos[trie[1][i]] = extend(i, 1);
    while (Q.size()) {
        int t = Q.front();
        Q.pop();
        for (int i = 0; i < 26; i ++ )
            if (trie[t][i])
                Q.push(trie[t][i]), pos[trie[t][i]] = extend(i, pos[t]);
    }
}

int main() {
    int T;
    scanf("%d", &T);
    while (T -- ) {
        string s;
        cin >> s;
        ins(s);
    }
    build();
    long long ans = 0;
    for (int i = 2; i <= tot1; i ++ )
        ans += node[i].len - node[node[i].fa].len;
    printf("%lld\n%d\n", ans, tot1);
    return 0;
}