给出$n$个元素，他们组成了一些集合。

维护下列操作：

• 将两个元素所在集合合并
• 询问两个元素是否属于同一个集合

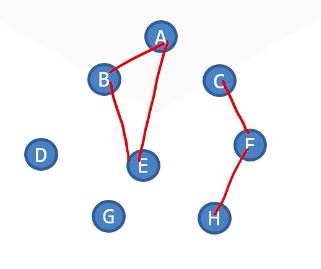
并查集是一个森林形的数据结构。
将一个元素抽象为一个图中的结点，保证同属一个集合的元素包含在同一棵树中，而不在同一个集合的元素分属不同的树。

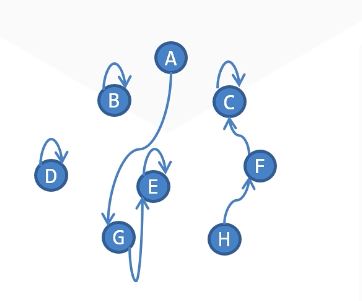
将每棵树组织成有根树的形式。
对每一个结点，只需记录它的父亲结点编号。为方便实现，令树根的父亲结点为它本身。

这样，每一个集合都可以用树根的结点编号来表示。查询两个元素所属集合是否相同，只需判断两个元素树中的根祖先是否相同。

初始化：

for (int i = 1; i <= n; ++i) 
    p[i] = i; 

给出点 $x$，询问 $x$ 所在树的根节点：

int root(int x) {
    if (x == p[x]) 
       return x;
    return root(p[x]);
}

将两个元素所在集合合并，就是把一个树根连到另一个树上。
注意：只能合并两个不同的集合！

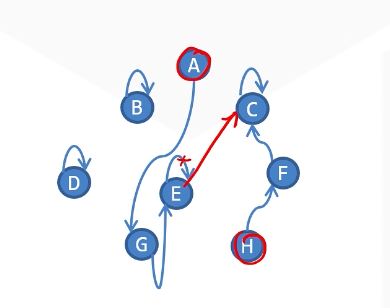
合并元素 $x$ 和 $y$ 所属集合：

int rx = root(x), ry = root(y);
if (rx != ry) 
    p[rx] = ry;

以上，单次操作时间复杂度均为$O(n)$，即一个集合形成一条链的情形。

改进

路径压缩：

事实上，我们不关心树具体是什么样子，而只关心每个结点的根祖先是什么。
所以，当访问到一条长链时，不妨让链上元素都直接连到根结点上。

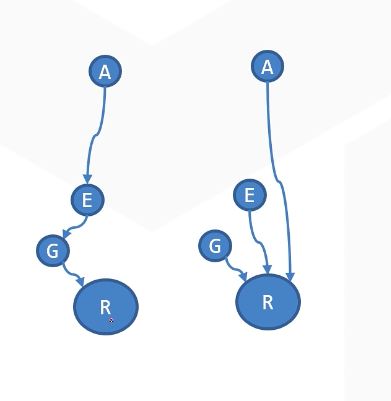
int root(int x) {
    if (x == p[x]) return x;
    return p[x] = root(p[x]);
}

按秩合并：

还可以在合并的过程中提前避免产生长链。
保存每个树的高度。在合并的过程中，让较高的树的祖先作为新的祖先，从而尽量防止树的高度变大。

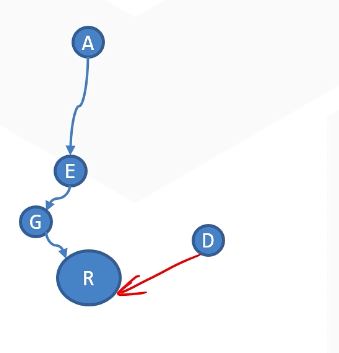
单独使用任何一种优化，可以让单次操作时间（均摊）复杂度均为$𝛰(logn)$。

同时使用两种优化，单次操作时间均摊复杂度可降至$O(\alpha(n))$，其中$𝛼$表示反阿克曼函数。

带权并查集

概念：在并查集的边上加上一些信息进行维护就是带权并查集。

原理：并查集的边上存储与父亲结点有关的信息，一般需要满足可以向上合并，这样在路径
压缩时就可以合并信息到新的边上，至于合并操作，一般会给出要合并的两个结点之间的相
对关系，合并集合时根据以下关系实现：

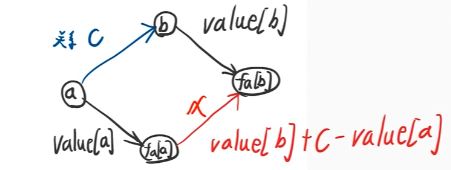
如图所示，给出关系c后，可以画出这样一个四边形，图中有2条路径可以从a到fa[b]而他们路径上的权值和（此处以求和为例）应该是相等的，这样就可以列出方程
$$value[a]+x=value[b]+c$$
移项后得到的就是合并时边权的取值$x$。

一些练习题：

1、 亲戚
2、 【模板】并查集
3、 A Bug’s Life
4、 食物链
5、 信息传递
6、 银河英雄传说
7、 等式方程的可满足性
8、 村村通
9、 How Many Answers Are Wrong
10、被围绕的区域
11、修复公路
12、 保证图可完全遍历
13、 朋友
14、 Friends
15、 Connect Cities
16、 Peaceful Rooks
17、 1 or 2
18、 省份数量
19、 执行交换操作后的最小汉明距离
20、 冗余连接