二分模板

其实二分模板网上特别多，但是在用了y总的模板过后就离不开了，亲测好用，下面结合自己的使用体验和理解做一个总结。

模板一

int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    return l;
}

模板二

int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

模板理解

上面的模板其实分别对应于两类问题

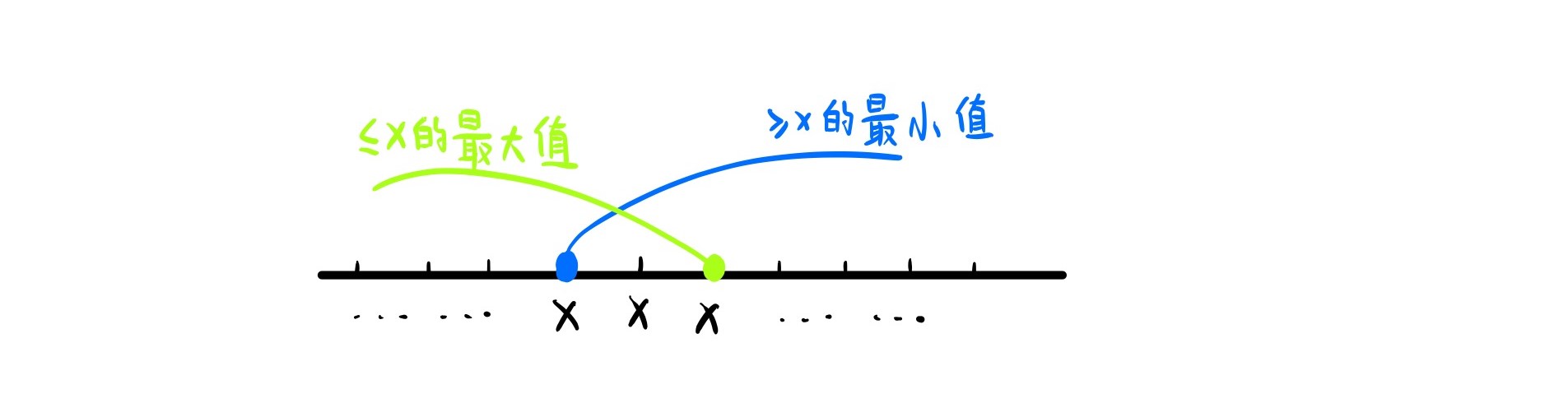
• 模板一： 找到大于等于x的最小的数
• 模板二： 找到小于等于x的最大的数

注意： x不一定是我们所要求的目标值，x的选择目的是为了让我们的区间一分为二，具体关于x的选择大家可以根据下面的题目加以理解。

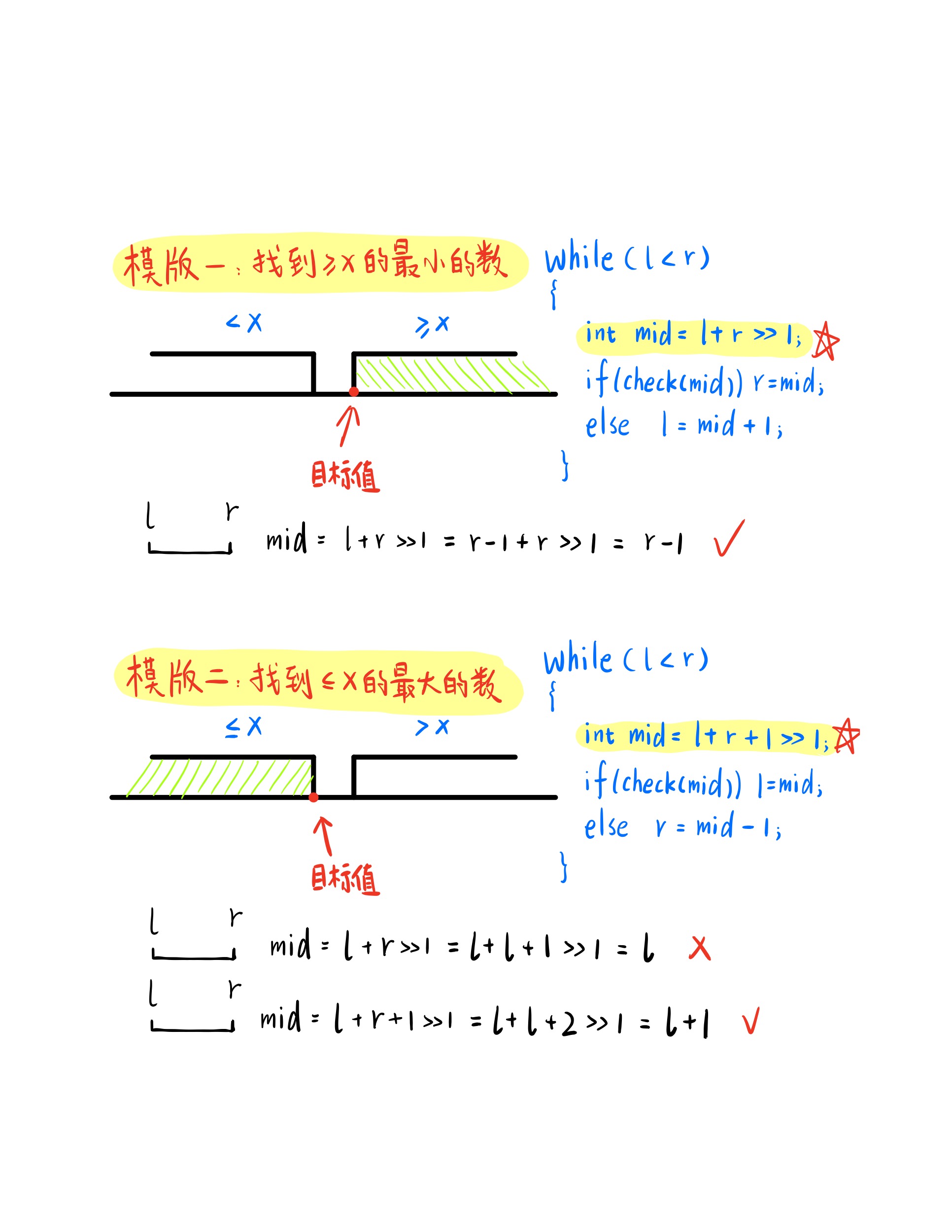
重点：

• while循环中的循环条件为l < r,切忌不可等于！但是如果是其他模板，可能会不一样。
• 在求中点mid的时候，l + r >> 1等价于(l + r) / 2，因为在计算机中位运算会比较快。
• check(mid)是判断我们的终点是否满足某种性质，对于模板一，我们需要找到>=x的最小的数，因此整个右侧区间，即>=x的区间都是满足check条件的。对于模板二，我们需要找到<=x的最大的数，整个左侧区间，即<=x的区间是满足check条件的。
• 在模板二中，中点mid的更新方式为mid = l + r + 1 >> 1, 这是因为我们的目标值处于左侧区间的右端点，当每次缩小我们的搜索区间时，我们的区间都是在向我们的目标值靠拢，直到最后我们的区间缩小到一个点时，即为我们的目标值。在这个过程中，由于我们while循环的条件为l < r,所以当我们的区间还没有缩小到一个点时，若此时刚好r = l + 1，且r恰好是我们左侧区间的右端点时，由于c++语法中的/运算符或是>>运算符，默认都是下取整，所以mid = l + r >> 1 = l + l + 1 >> 1 = l。又在模板二中，我们更新的l = mid,就会发现我们的l不会向右靠近，我们的l永远都到不了我们的目标值了。所以为了让我们的l每次都能向目标靠近一点点，所以更新中点时应为mid = l + r + 1 >> 1。
• 在模板一中如果出现上述情况，当l = r - 1，且l恰好是右侧区间的左端点时，更新mid = l + r >> 1 = r - 1 + r >> 1 = r - 1,然后更新r = mid时发现很幸运的是我们的r在这种情况下还是会向目标靠近，因此我们没什么好操心的了。

对于上述的文字可能理解起来还是很晦涩，但是用几道简单的题目上手后就很通透了。

例题

LeetCode 34. 在排序数组中查找元素的第一个和最后一个位置

题目描述

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

你的算法时间复杂度必须是$O(log n)$ 级别。

如果数组中不存在目标值，返回[-1, -1]。

示例 1:

输入: nums = [5,7,7,8,8,10], target = 8
输出: [3,4]

示例 2:

输入: nums = [5,7,7,8,8,10], target = 6
输出: [-1,-1]

算法分析

根据题意，其实就是要我们求出一段包含所有给定目标值的区间，并返回该区间的左右端点。因此我们直接套用上面的模板一和二，即可求出答案，当我们第一次求某一侧端点时，需要看一下它的值是不是等于我们的目标值，如果不相等，说明数组中并不存在我们要找的数，此时即可返回[-1, -1]了。

C++代码

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        vector<int> res;
        if (!nums.size()) return {-1, -1};

        int l = 0, r = nums.size() - 1;
        while (l < r)
        {
            int mid = l + r >> 1;
            if (nums[mid] >= target) r = mid;
            else l = mid + 1; 
        }
        if (nums[l] != target) return {-1, -1};
        res.push_back(l);
        l = 0, r = nums.size() - 1;
        while (l < r)
        {
            int mid = l + r + 1 >> 1;
            if (nums[mid] <= target) l = mid;
            else r = mid - 1;
        }
        res.push_back(r);
        return res;
    }
};

LeetCode 69. x 的平方根

题目描述

实现int sqrt(int x)函数。

计算并返回x的平方根，其中x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例 1:

输入: 4
输出: 2

示例 2:

输入: 8
输出: 2
说明: 8 的平方根是 2.82842…,由于返回类型是整数，小数部分将被舍去。

算法思路

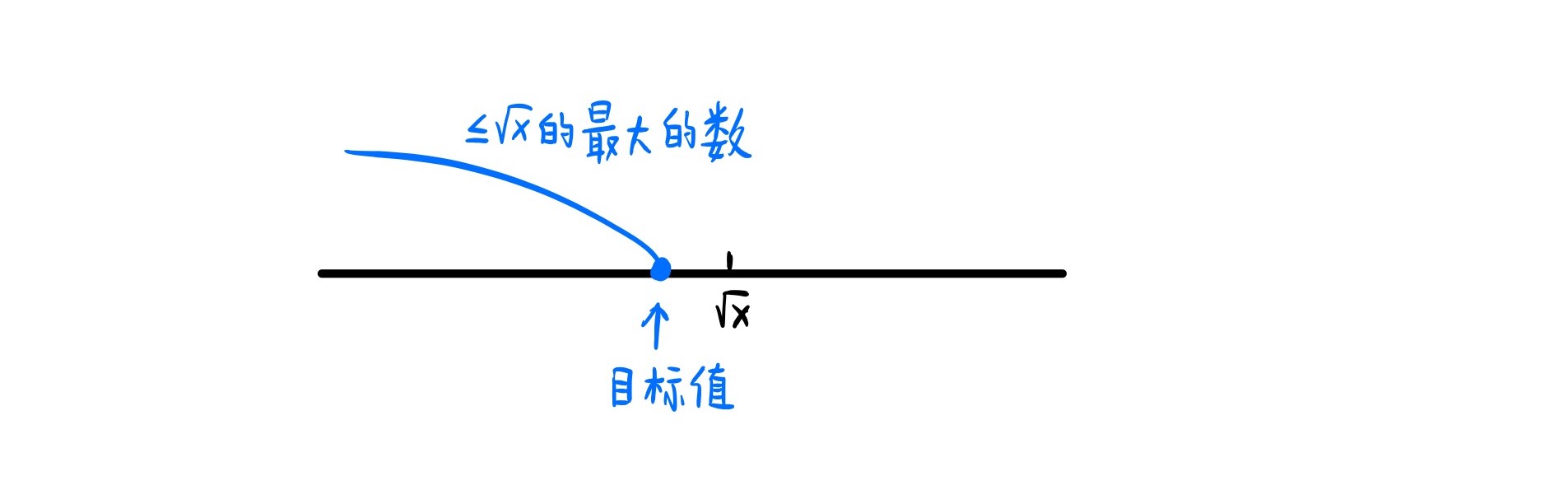
该题需要返回一个数x平方根的整数部分，如果一个数的平方根刚好是整数，那么我们的答案就是根号x,但是如果根号x是一个小数的话，我们需要返回的就是小于根号x的最大的整数，因此将上述两种情况合并起来，就可以得到和上面一样的二分求解区间，继续套用我们的模板二，即可求解。

class Solution {
public:
    int mySqrt(int x) {
        int l = 0, r = x;

        while(l < r)
        {
            int mid = l + (long long)r  + 1 >> 1;
            if(mid <= x / mid) l = mid;
            else r = mid -1;
        }
        return r;
    }
};

LeetCode 153. 寻找旋转排序数组中的最小值

题目描述

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

请找出其中最小的元素。

你可以假设数组中不存在重复元素。

示例 1:

输入: [3,4,5,1,2]
输出: 1

示例 2:

输入: [4,5,6,7,0,1,2]
输出: 0

算法分析

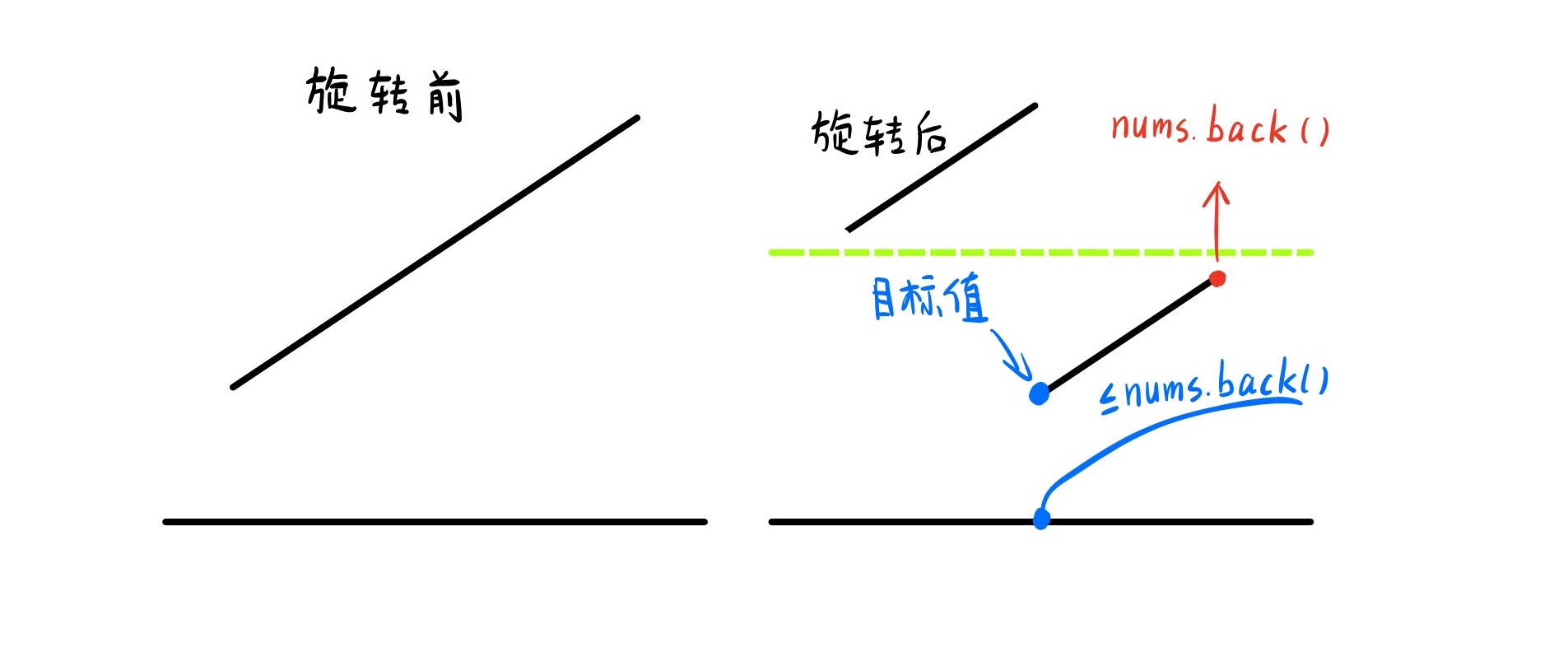
该题给了一个旋转后的排序数组，旋转前该数组由于是排序的，因此最小值就是第一个元素。但是现在由于旋转的缘故，该最小值被旋转到了数组的中间，根据下图可以清楚地看到，由于数组中没有重复元素，因此旋转后的数组出现了断层。在前半部分的所有数的大小都在断层之上，后一部分的值都在断层之下。也就是这一断层的出现，将我们的区间分成了两部分，其实前半部分都是大于最后一个元素的，后半部分都是小于等于最后一个元素的。而我们所要求解的最小值就是满足小于等于最后一个元素的右侧区间的左端点。分析到这，因此又是直接上模板。

C ++代码

class Solution {
public:
    int findMin(vector<int>& nums) {
        if(nums.empty()) return 0;

        int l = 0, r = nums.size();

        while(l < r)
        {
            int mid = l + r >> 1;
            if(nums[mid] <= nums.back()) r = mid;
            else l = mid + 1;
        }

        return nums[r];

    }
};