前期准备:

我们先手写一个树，便于后续的调用。直接用即可，这里不作过多解释。

typedef char BTDataType;
typedef struct BinaryTreeNode
{
    struct BinaryTreeNode* left;
    struct BinaryTreeNode* right;
    BTDataType data;
}BTNode;

BTNode* BuyNode(BTDataType x)
{
    BTNode* node = (BTNode*)malloc(sizeof(BTNode));
    if (node == NULL)
    {
        printf("malloc fail\n");
        exit(-1);
    }

    node->data = x;
    node->left = node->right = NULL;
    return node;
}

BTNode* CreatBinaryTree()
{
    BTNode* nodeA = BuyNode('A');
    BTNode* nodeB = BuyNode('B');
    BTNode* nodeC = BuyNode('C');
    BTNode* nodeD = BuyNode('D');
    BTNode* nodeE = BuyNode('E');
    BTNode* nodeF = BuyNode('F');
    nodeA->left = nodeB;
    nodeA->right = nodeC;
    nodeB->left = nodeD;
    nodeC->left = nodeE;
    nodeC->right = nodeF;
    return nodeA;
}

上述实现的效果如下:

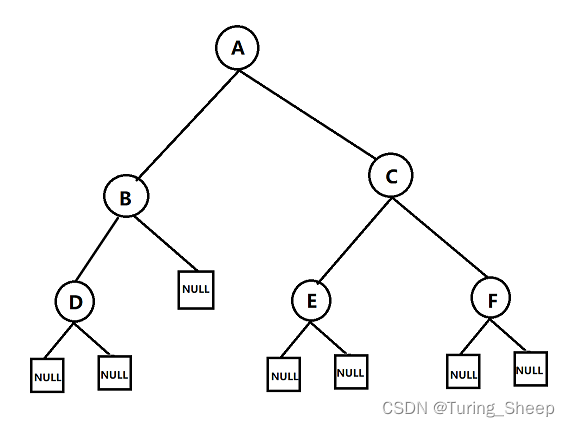
那么我们如何去遍历上述树中的每一个元素呢？接下来的内容将解决这个问题。

==（遍历的顺序取决于根节点的位置）==

一、前序遍历

1、遍历的思路

前序遍历的顺序是：根节点----->左子树----->右子树。

那么上述树型结构中，我们的前序遍历的顺序是：

A—>B—>D—>NULL—>NULL—>NULL—>C—>E—>NULL—>NULL—>F—>NULL—>NULL

2、遍历代码

void PreOrder(BTNode* root)
{
    if(root==NULL)
    {
        printf("NULL ");
        return;
    }
    printf("%c ",root->data);
    PreOrder(root->left);
    PreOrder(root->right);
}

3、遍历图示

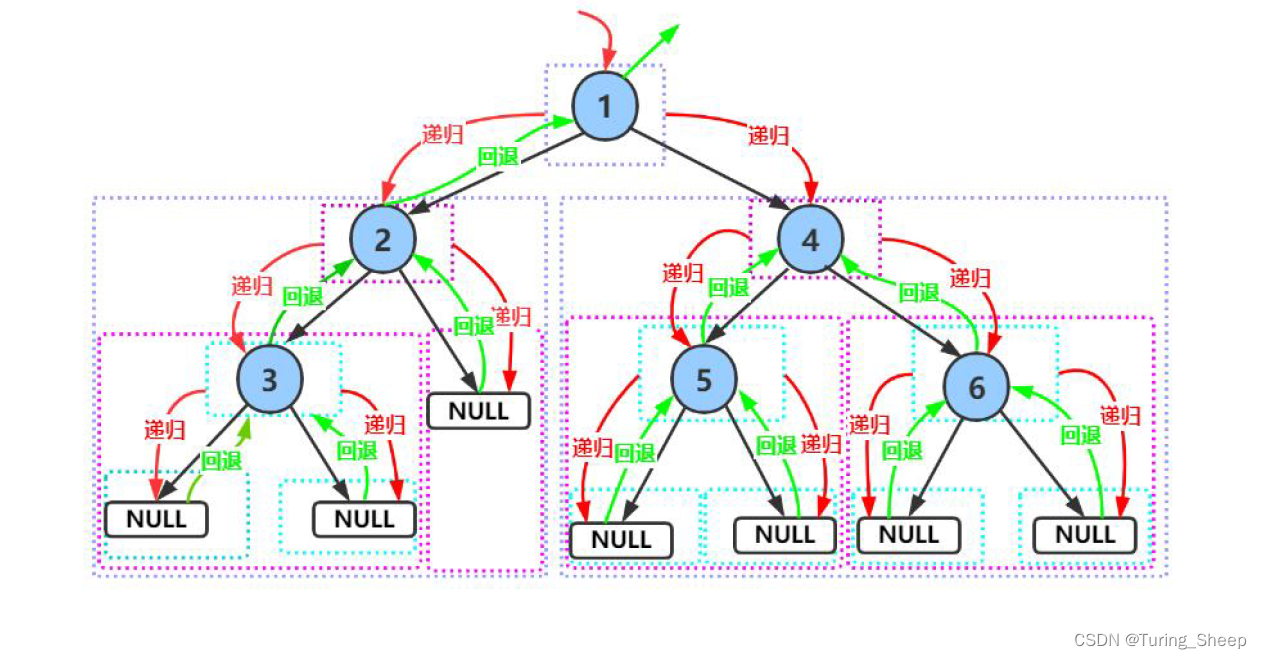
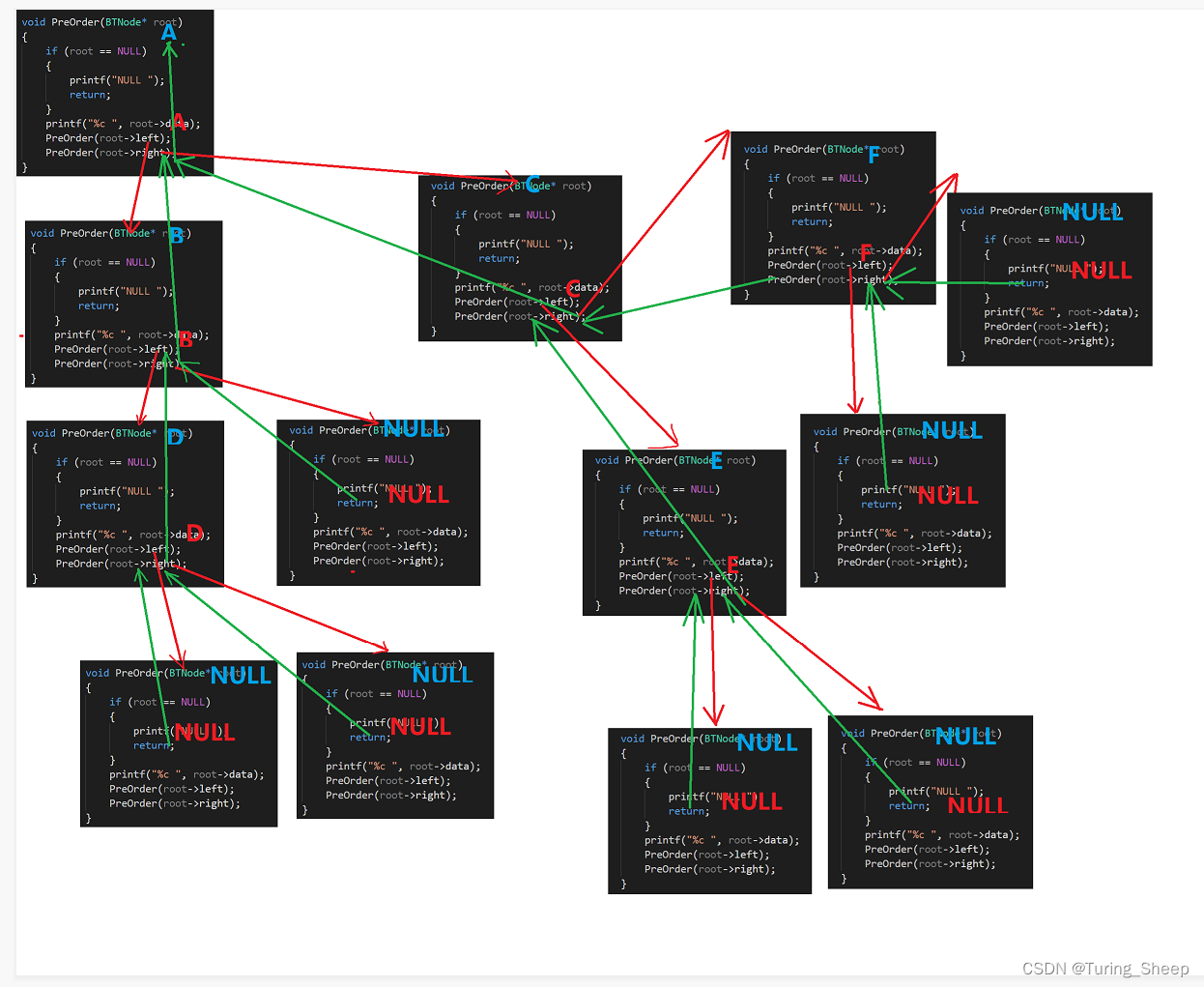
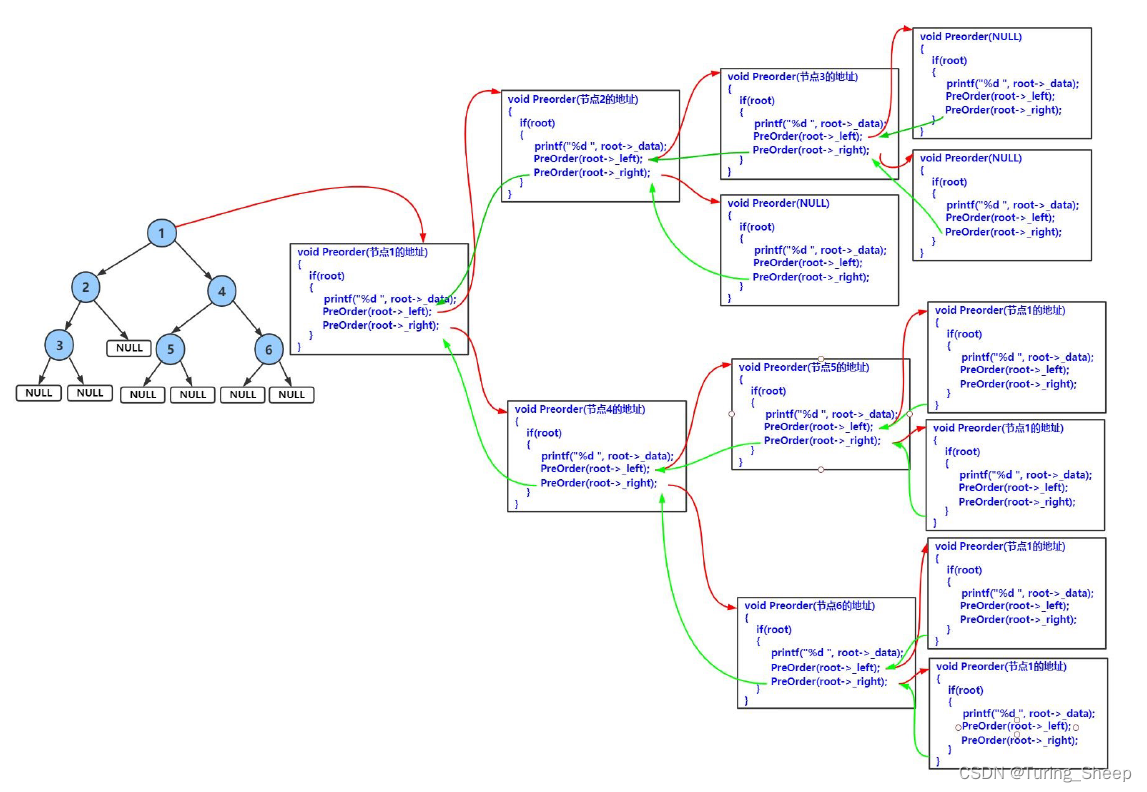
二、中序遍历

1、遍历的思路

中序遍历的顺序是：左子树----->根节点----->右子树

那么上述树型结构中，我们的中序遍历的顺序是：

NULL—>D—>NULL—>B—>NULL—>A—>NULL—>E—>NULL—>C—>NULL—>F—>NULL

2、遍历代码

void InOrder(BTNode* root)
{
    if(root==NULL)
    {
        printf("NULL ");
        return;
    }
    InOrder(root->left);
    printf("%c ",root->data);
    InOrder(root->right);
}

图这里就不画了，大家自己画吧，这样可以锻炼一下自己的画图能力。（其实是作者有点累了）

三、后序遍历

1、遍历的思路

后序遍历的顺序是：左子树----->右子树----->根节点

那么在上述的图片中，后序遍历的顺序是：

NULL—>NULL—>D—>NULL—>B—>NULL—>NULL—>E—>NULL—>NULL—>F—>C—>A

2、遍历代码

void PostOrder(BTNode* root)
{
    if(root==NULL)
    {
        printf("NULL ");
        return;
    }
    PostOrder(root->left);
    PostOrder(root->right);
    printf("%c ",root->data);

}

图这里就不画了，大家自己画吧，这样可以锻炼一下自己的画图能力。（其实是作者有点累了）

三、遍历的应用

1、计算二叉树中的节点个数

二叉树中的节点个数等于根节点加上左子树中的节点个数再加上右子树的节点个数，基于这种思路，我们写下了如下的函数：

int BinaryTreeSize(BTNode*root)
{
    if(root==NULL)return 0;
    return BinaryTreeSize(root->left)+BinaryTreeSize(root->right)+1;
}

2、二叉树叶子节点的个数

二叉树中的叶子节点的个数等于左子树中叶子节点的个数加上右子树的叶子节点中的个数，我们利用上述的思路可以写出下面这个递归函数。

int BinaryTreeLeafSize(BTNode*root)
{
    if(root==NULL)return 0;
    if(root->left==NULL&&root->right==NULL)return 1;
    return BinaryTreeLeafSize(root->right)+BinaryTreeLeafSize(root->left);
}

3、二叉树的深度

二叉树等于根节点的高度加上左右子树中较高的高度，根节点自身的高度是1，所以二叉树的高度就等于1+左右子树中较高的高度。

int BinaryTreeDepth(BTNode*root)
{
    if(root==NULL)return 0;
    int depth=max(BinaryTreeDepth(root->left),BinaryTreeDepth(root->right));
    return depth+1;
}

4、二叉树中第K层的节点个数

第K层的节点数＝左子树第k-1层的节点数+右子树第k-1层的节点数，基于这个式子我们写出下面的递归函数。

int BinaryTreeLevelKSize(BTNode* root, int k)
{
    if(root==NULL)return 0;
    if(k==1)
    {
        return 1;
    }
    return BinaryTreeLevelKSize(root->left,k-1)+BinaryTreeLevelKSize(root->right,k-1);
}

5、二叉树查找值为X的节点

先查根节点，再查左子树，再查右子树。

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
    if(root==NULL)return NULL;
    if(root->data==x)return root;
    BTNode*left=BinaryTreeFind(root->left,x);
    if(left)return  left;
    BTNode*right=BinaryTreeFind(root->right,x);
    if(right)return right;
    return NULL; 
}