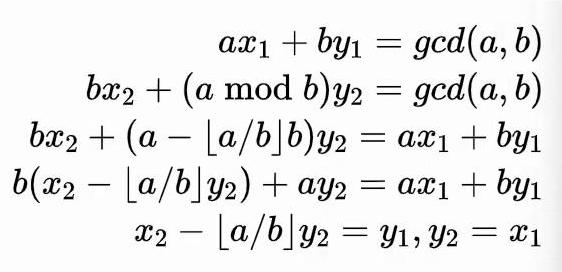概念引入：

整除:

整数b能被整数a整除，即$\frac{b}{a}$是一个整数，那么称为 $a~$整除$b$ 或 $b~$能被$a$整除，记作：
$$a~|~b$$

因数

对于任意整数$x$，如果存在$a~|~x$，那么称$x$是$a$的一个因数(亦称因子或约数)

最大公因数

对于整数$a,~b$，它们的最大公因数(这里设为$k$，是整数)是使得$k~|~a~并且~k~|~b$的最大数。
记为$(a,~b)$。
特别地：规定当$b=0$时$(a,~b)=(a,~0)=a$。
欧几里得算法正是求最大公因数的

余数

如果整数b不能被整数a整除，即$a \nmid b$，则一定存在整数$k,~r$，使得$b=a*k+r~~~(0<r<a)$，我们称$r$为余数。

欧几里得算法

定理：两个整数的最大公约数等于其中较小的那个数和两数相除余数的最大公约数

字母表示为：
$$(a,~b)~=~(b,~r)~~~~(a>b.a,b,r∈\mathbb{Z},r是a除以b的余数)$$

证明：
$a$可以表示成$a = kb + r~(不妨设a,b,k,r∈\mathbb{N^*},~~0<r<b)$
假设$d$是$a,b$的一个公约数，记作$d|a,d|b$，即$a$和$b$都可以被$d$整除。
而$r = a - kb$，两边同时除以$d，\frac{r}{d}=\frac{a}{d}-\frac{kb}{d}$，因为$d$是$a,b$最大公因数，所以等式右边是整数，所以左边也是整数，即$\frac{r}{d}$为整数，因此$d|r$
因此$d$也是$b, r$的公约数。
因$(a,b)$和$(b,r)$的公约数相等，则其最大公约数也相等，得证。

补充：扩欧构造