目录

1.一元二次方程的定义

2.一元二次方程的求解

3.一元二次方程的性质

4.一元二次方程的构造

5.一元二次方程的更多表达方法

6.一元二次方程的几何背景

7.解一元二次方程的常见问题

如有错误，请指出!

一元二次方程的定义

形如$ax^2+bx+c=0~~(a≠0)$的方程叫做一元二次方程

一元二次方程有两个解，称为两个根，一般记为$x_1,~x_2$
方程根有以下三个情况：
1.方程有两个不同的根，即$x_1 ≠ x_2$
2.方程有两个相等的根，即$x_1 = x_2$，此时称方程的根为二重实根
3.方程在实数范围内无解

一元二次方程的求解

1.公式法

$ax^2+bx+c=0~~(a≠0)$的求解公式:
$$\frac{-b±\sqrt{Δ}}{2a}$$
其中$Δ=b^2-4ac$，称为根的判别式($Δ$是希腊字母德尔塔的小写形式)
我们发现：
$Δ > 0$时，代入公式有两个结果，对应上文根的情形1
$Δ = 0$时，公式有一个结果，对应2
$Δ < 0$时，由于根号为负数，所以公式无意义，对应3
$Δ$是完全平方数时，两个根一定是有理数，否则是无理数
所以在解一元二次方程的时候，可以先看看$Δ$的取值，进而分析根

公式法的利弊：
利：无脑方便
弊：缺乏技巧

2.十字相乘

价值

十字相乘是分解因式的重要方法之一，它的价值在于确定一个一元二次方程是由哪两个一元一次方程相乘得来的，当确定下来两个因式后，方程的解不言而喻。
例如：
$$x^2+2x+1=0 \iff (x+1)(x+1)=0$$
所以$x_1=x_2=-1$
$$x^2+x-6=0 \iff (x+3)(x-2)=0$$
所以$x_1=-3,~x_2=2$
$$2x^2-5x-3=0 \iff (2x+1)(x-3)=0$$
所以$x_1=-\frac{1}{2},~x_2=3$
即当$x$使得两个因式其中一个等于$0$时就是一个根
此时$0$乘任何数等于$0$

方法

懒得敲代码，遂手画图

这里有个详细图解解释

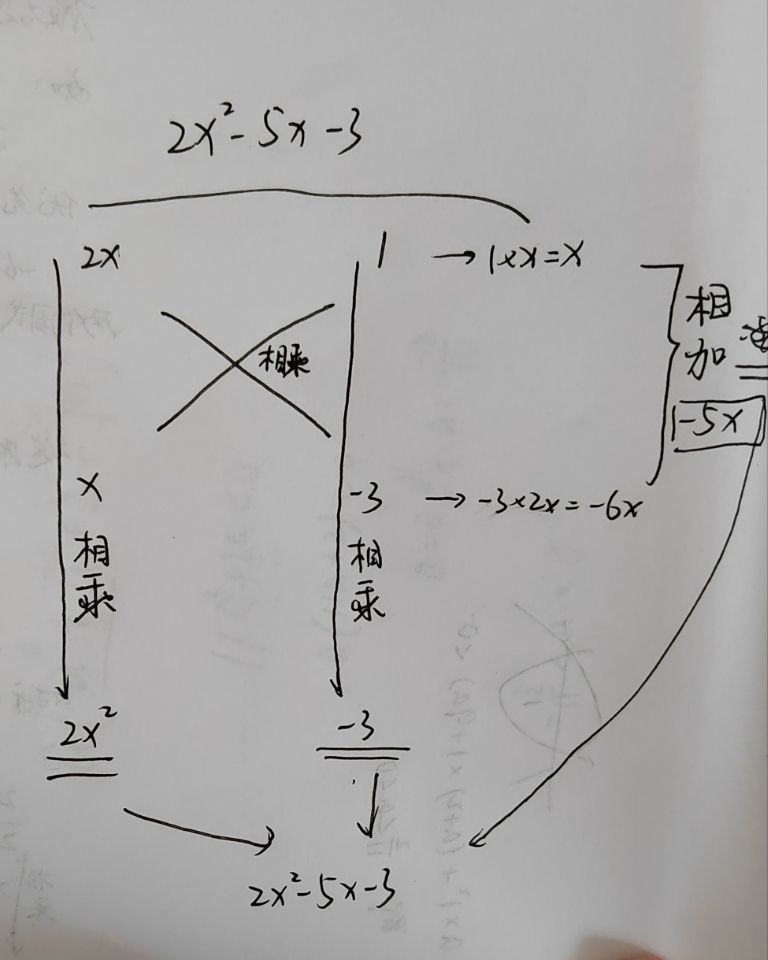
建议多多练习十字相乘，掌握技巧！

3.特殊值法(进阶)

顾名思义，代入特殊值
这里先给出一个命题:
若多项式$f(x)$满足$f(a)=0,~~a∈\mathbb{R}$ 则$(x-a)|f(x)$

如$x^2-3x+2=0$，发现$x=2$时方程成立
所以方程一定可以分解成$(x-2)*F(x)$的形式，其中$F(x)$是一次的
接下来，我们可以使用长除法解决

一元二次方程的性质

韦达定理

设一元二次方程$ax^2+bx+c=0~~(a≠0)$的解为$x_1,~x_2$，则
$$x_1+x_2=\frac{-b}{a}$$
$$x_1x_2=\frac{a}{c}$$
证明方法：使用求根公式

拓展

根据韦达定理可知
$$|x_1-x_2|=\frac{\sqrt{Δ}}{|a|}$$

一元二次方程的构造

对于实数$a,~b$，总是可以构造出一元二次方程，使得该方程两个根分别为$a,~b$。它是
$$x^2-(a+b)x+ab=0$$
不难看出，方程等价于
$$(x-a)(x-b)=0$$
于是可得方程根
价值：
如：若知道$a+b,~ab$的值，则可以通过该方程$Δ>0$来获得信息

一元二次方程的更多表达方法

1.交点式

设一元二次方程$ax^2+bx+c=0~~(a≠0)$的解为$x_1,~x_2$，则方程等价于
$$a(x-x_1)(x-x_2)=0$$
称它为交点式
使用韦达定理易证

2.顶点式

利用配方法，总是可以将$ax^2+bx+c=0~~(a≠0)$化为$(x-k)^2+t=0$的形式
因为$a≠0$，所以

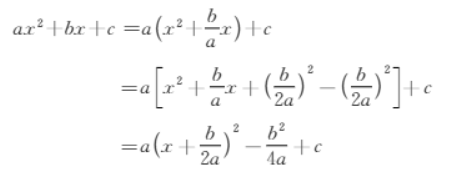
这样的式子称为顶点式，我们可以通过顶点式确定一个二次函数的对称轴$(x=\frac{-b}{2a})$和顶点坐标$(\frac{-b}{2a},~\frac{4ac-b^2}{4a})$

一元二次方程的几何背景

在平面直角坐标系下，一个一元二次方程图像相当于抛物线，而方程$=0$的解反映在坐标系下就是抛物线与$x$轴的交点，即$y=0$时$x$的值
图例

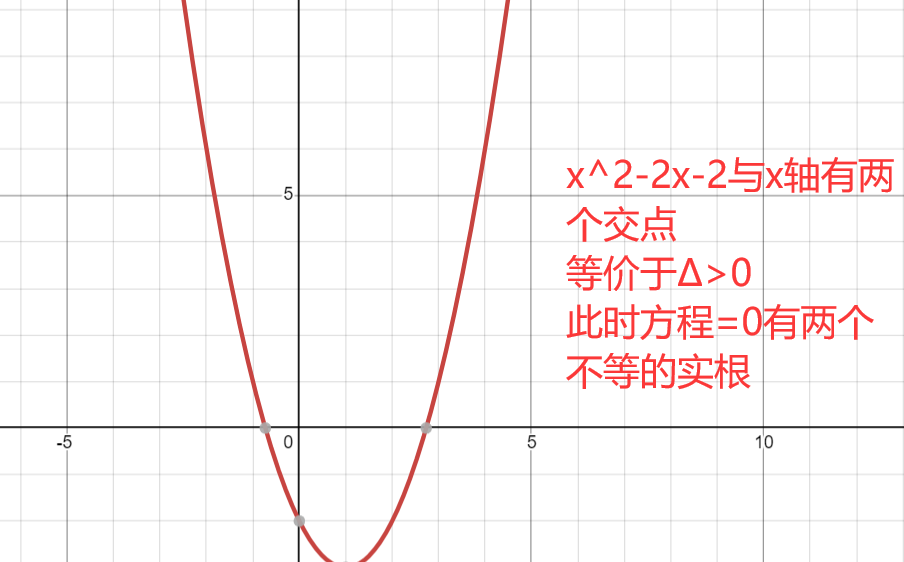
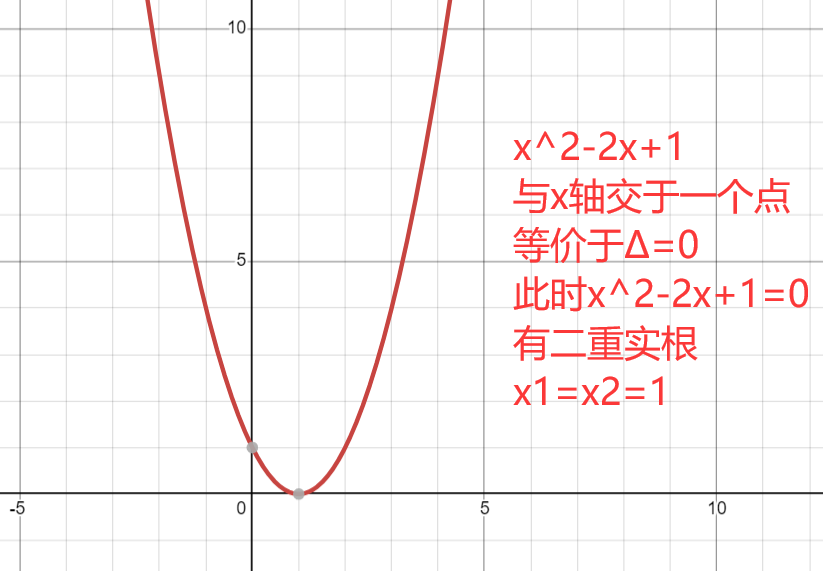
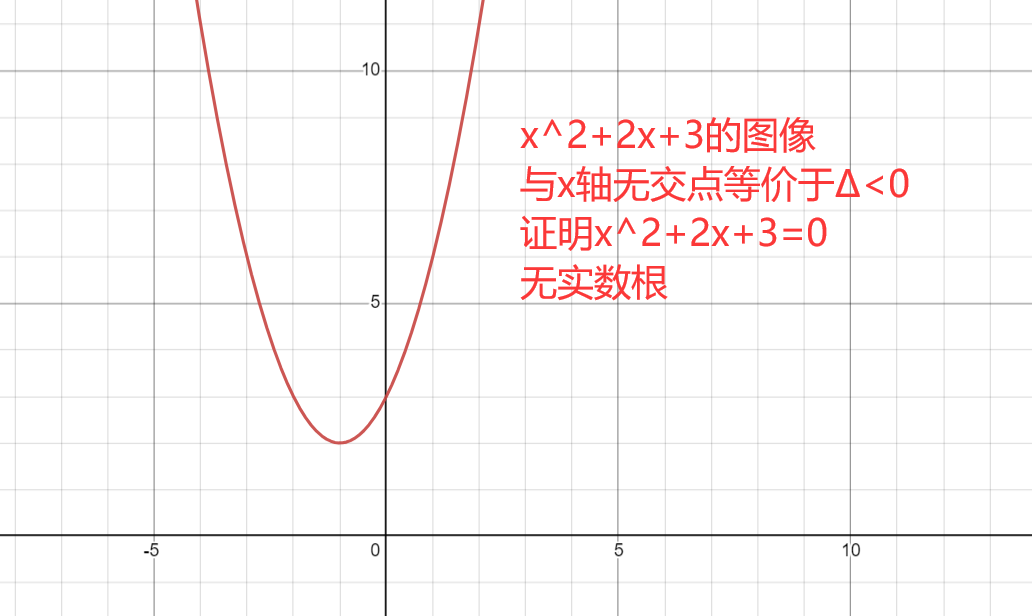
在求一元二次方程区间最值时，往往需要转化为二次函数，借助函数图像求解。

解一元二次方程的常见问题

注：个人经验仅供参考

1.含参

在解二次项系数含参问题时，需要着重注意参数，讨论系数正负、是否等于$0$等情况

坑点：注意题目所求，如果是“在方程$f(x)$中”，则二次项系数可以为$0$，如果为“在二次方程$f(x)$中”，则不能

2.整数根问题

一个一元二次方程两个根都是整数意味着$Δ$为完全平方数。通常以此为突破口，通过构造完全平方式，利用平方差，因式分解的手段解决。
如$x^2+(a-6)x+a=0$的两根为整数，求$a$值
第一步： $~Δ=(a-6)^2-4a$为完全平方数，不妨设为$t^2~~(t∈\mathbb{N})$
第二步，构造完全平方式： $~(a-6)^2-4a=a^2-16a+36=(a-8)^2-28=t^2$
第三步，利用平方差：
$$~(a-8)^2-28=t^2 \iff (a-8)^2-t^2=28 \iff (a-8-t)(a-8+t)=28$$
第四步，因式分解： 显然$~(a-8-t)~$和$~(a-8+t)~$同奇偶，所以将$28$的因式分解分为$(2,14),~(-14,-2)$两种情况，分别对应$~(a-8-t)~$和$~(a-8+t)~$，因为$t$为自然数，显然前者小于后者
第五步： 解此二元一次方程组，获得$a$值

3.“二元二次方程”

解此类问题时，主元法是值得尝试的，即把一个元看作主元，另一个看作参数，转化为一元二次方程。
如在寻找$x^2+xy+2y^2=29$的正整数解时，可以把$x$看为主元:
$$x^2+xy+2y^2=29 \iff x^2+yx+(2y^2-29)=0$$
因为是正整数解，所以$Δ=y^2-4(2y^2-29)$为完全平方数，可通过2.解决

4.含参的一元二次不等式

此类问题少不了分类讨论，但分类讨论时很容易迷糊。对此我们可以找临界点
那么什么算是临界点？下面有3个常见的：

1.若二次项系数含参，则系数=0为一个临界点

因为它关系到二次函数的开口朝向，与是否降级变为一次函数。需要将系数与0的关系转化为参数与0的关系，移项即可
当系数<0时，开口朝下，系数>0时开口朝上
系数=0时：
如果不等式中仍含有未知数，正常解即可
如果没有了，那么化简看常数不等式是否成立，成立则无穷解，不成立则无解

2.$Δ=0$为一个临界点

关系着二次方程根的情形，下面会有例子演示。

3.如果只确定一个根，则该根为临界点

关系到另一个根与其位置关系，进而关系到解集表示方法。需讨论另一个含参根与其大小关系。
如果可以分解因式，那么可以快速看出是否符合该情形

确定临界点后，在数轴上从左往右依次讨论$(-\infty,最左临界点)，临界点值，(临界点,下一个临界点)，(最右临界点,+\infty)$，一个也不能落下

例子：

$$f(x) = ax^2-ax+1>0 ~ 求x取值范围$$
二次项含参，则0为一个临界点
$Δ=0$时$a=4$，4为一个临界点
两根无法确定，故不讨论。
因此，我们需要讨论以下5种情况：
$a<0$, $a=0$, $0<$$a<4$, $a=4$, $a>4$

$\textit{upd } 2023.1.30$ 添加了性质、构造、更多表达方法、常见问题的模块，补充了几何背景模块
$\textit{upd } 2023.2.17$ 部分题面描述更清晰