LeetCode 46. 全排列

算法思路

dfs + 回溯解题框架

dfs算法的过程其实就是一棵递归树，所有的dfs算法的步骤大概有以下几步：

• 找到中止条件，即递归树从根节点走到叶子节点时的返回条件，此时一般情况下已经遍历完了从根节点到叶子结点的一条路径，往往就是我们需要存下来的一种合法方案
• 如果还没有走到底，那么我们需要对当前层的所有可能选择方案进行枚举，加入路径中，然后走向下一层
• 在枚举过程中，有些情况下需要对不可能走到底的情况进行预判，如果已经知道这条路不可能到达我们想去的地方，那我们干嘛还要一条路走到黑呢，这就是我们常说的剪枝的过程
• 当完成往下层的递归后，我们需要将当前层的选择状态进行清零，它下去之前是什么样子，我们现在就要让它恢复原状，也叫恢复现场。该过程就是回溯，目的是回到最初选择路口的起点，好再试试其他的路。

将上面的算法框架应用于对于本题，根据习惯，枚举时我们可以选择每个位置放哪个数，同时也可以枚举每个数放在哪个位置。 不同枚举顺序，就会画出不同的递归搜索树（如下图），接下来我们就分别分析以下两种情况：

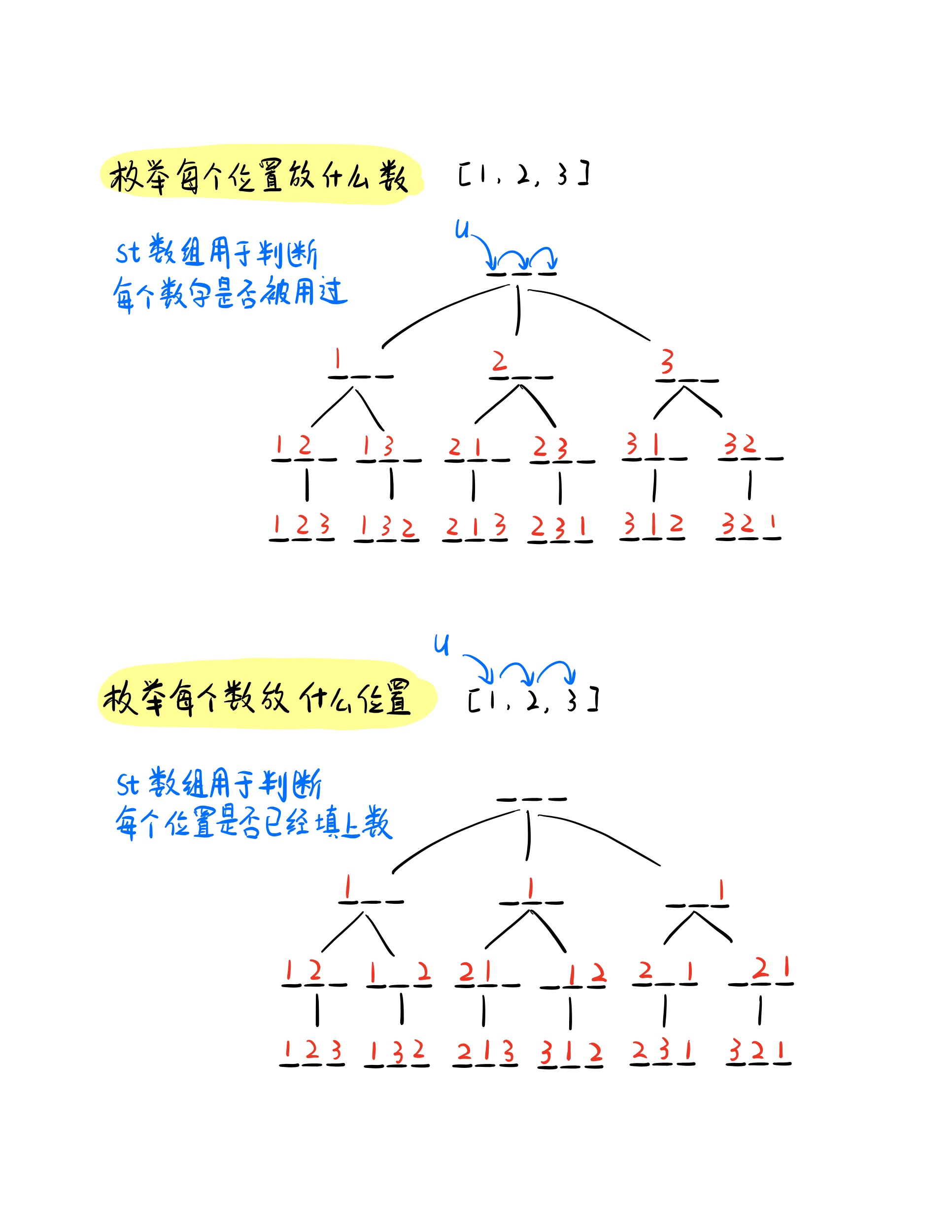
枚举每个位置放什么数

1. 因为我们需要枚举每个位置放什么数，因此当我们每个位置都放好数，我们就走到了递归树的叶子节点，此时将我们的该路径加入方案中。

2. 如果还没有到达叶子结点，那么我们需要枚举选择该位置放哪些数，因为我们每个数都必须用且只能用一次，所以我们利用st数组来标记那些数被用过。枚举每一个数，如果没有用过，即可加入路径并标记，然后递归到下一层，即下一个位置。

3. 递归结束后，我们需要恢复现场，消除刚才的标记，并把刚才放在该位置上的数清空，即弹出。这样做的目的是因为当前位置上还可以选择放其他数，所以需要回到往下走之前的样子，然后再选择其他路。

C ++代码

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    vector<bool> st;
    vector<vector<int>> permute(vector<int>& nums) {
        st = vector<bool> (nums.size());
        dfs(nums, 0);
        return res;
    }

    void dfs(vector<int>& nums, int u) //u表示枚举到了方案数组path的哪个位置
    {
        if (u == nums.size()) //遍历完整个数组
        {
            res.push_back(path); //加入方案
            return;
        }

        for (int i = 0; i < nums.size(); i ++) //枚举当前位置可以选择哪些数
        {
            if (!st[i]) //没有选过
            {
                path.push_back(nums[i]); //选择该数
                st[i] = true; //标记选过
                dfs(nums, u + 1); //继续递归下一层
                st[i] = false; //回溯
                path.pop_back(); //回溯
            }

        }
    }
};

枚举每个数放哪个位置

1. 因为我们需要枚举每个数放什么位置，因此把所有数都放到了位置上，我们就走到了递归树的叶子节点，此时将我们的该路径加入方案中。

2. 如果还没有到达叶子结点，那么我们需要枚举当前数可以放在哪个位置，显然每个位置只能放一个数，所以我们利用st数组来标记那些位置上已经放好数了。枚举每个位置，如果没有放上任何数，即可在该位置放上数，然后递归到下一层，即继续去放下一个数。

3. 递归结束后，我们需要恢复现场，消除刚才的标记，由于只要当前位置的标记被清空，该位置就可以放数，所以当我们放下一个数时，如果发现该位置没有用过，即可放上去，此时刚好就能覆盖本来填上的数，因此位置上的数并没有必要清空。

C ++代码

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    vector<bool> st;
    vector<vector<int>> permute(vector<int>& nums) {
        path = vector<int> (nums.size());
        st = vector<bool> (nums.size());
        dfs(nums, 0);
        return res;
    }

    void dfs(vector<int>& nums, int u) //u表示枚举到了数组中的哪个数
    {
        if (u == nums.size()) //遍历完整个数组
        {
            res.push_back(path); //加入方案
            return;
        }

        for (int i = 0; i < nums.size(); i ++) //枚举每个位置
        {
            if (!st[i]) //如果该位置还没有放任何数
            {
                path[i] = nums[u]; //
                st[i] = true;
                dfs(nums, u + 1);
                st[i] = false;
            }
        }
    }
};

LeetCode 47. 全排列 II

算法思路

DFS + 回溯

与上一题不同的是，该题目给的数组里面可能出现相同元素。如果根据我们上题的做法，我们可以选择每个数可以放在哪些位置，同时我们也可以选择每个位置放哪些数，然后画出以下递归搜索树。

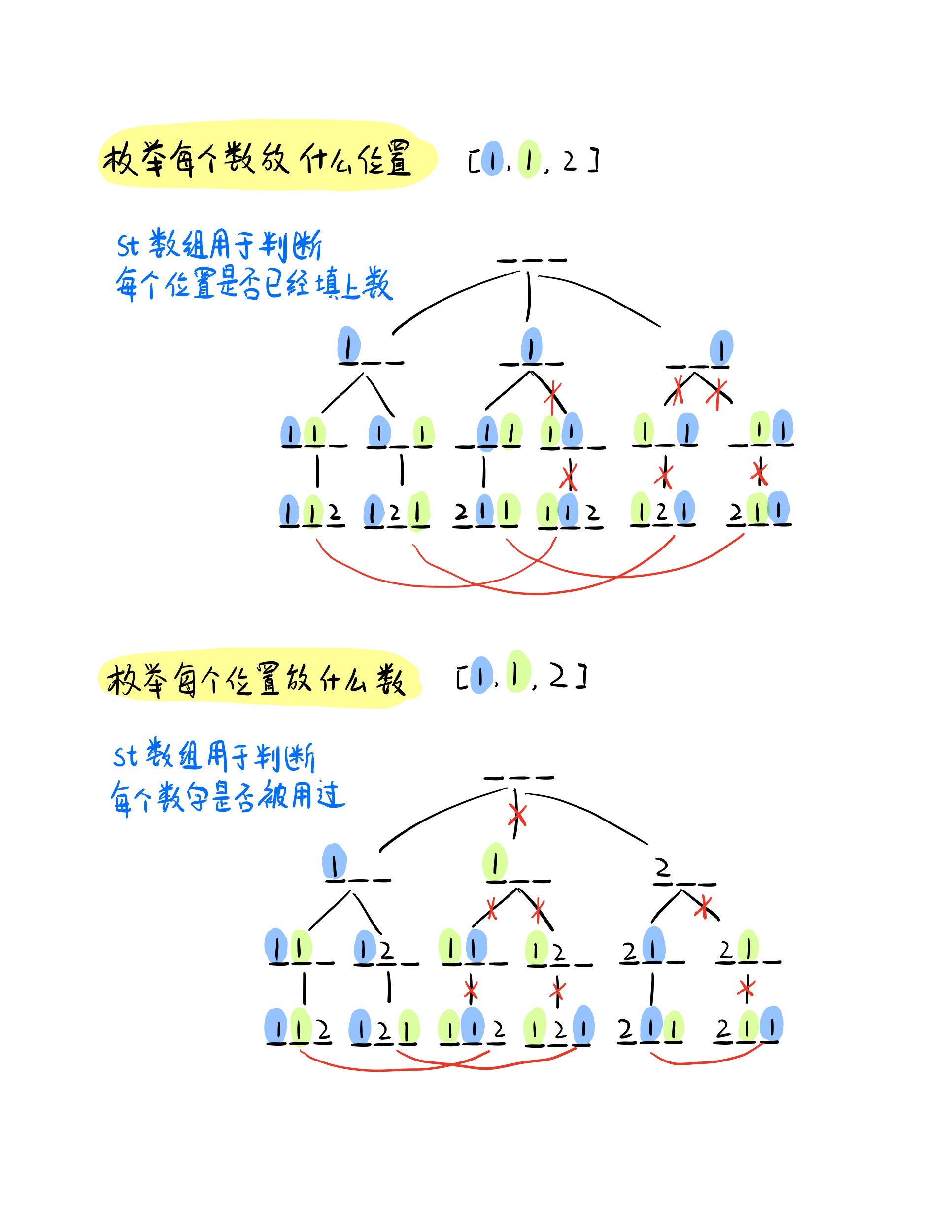
枚举每个数可以放在什么位置

如果把两个1当作不同的数，所有的方案就是下图中的叶子节点，但是很不幸，由于相同元素的出现，我们的最终方案也出现了重复。找到重复的情况，通过不同颜色的标记可以看出，对于相同的两个位置，蓝色的1在前或者绿色的1在前，方案只需要计算其中一个。因此我们可以人为地规定绿色的1只能出现在蓝色的1的后面，这样我们就可以避免重复方案了。

为了实现上述过程，我们需要将原数组中的元素进行排序，然后将原数组中元素之间的相对位置作为每一种方案中元素的相对位置。所以我们需要传入参数时添加一个参数start，该参数的意义是在枚举该数可以放哪些位置时，位置的枚举需要从start开始。这样当我们需要递归到下一层时，如果下一个选择的数和当前的数相等，因为在原数组中下一个数在当前数的后面，因此在放下一个数时也必须放在当前数的后面，因此传入参数start等于当前数所填位置的下一个位置。如果下一个数不同，那么就没有限制，位置枚举从0开始。

C ++代码

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    vector<bool> st;
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int n = nums.size();
        path = vector<int> (n);
        st = vector<bool> (n);
        dfs(nums, 0, 0);
        return res;
    }

    void dfs(vector<int>& nums, int u, int start)
    {
        if (u == nums.size())
        {
            res.push_back(path);
            return;
        }

        for (int i = start; i < nums.size(); i ++) //枚举哪个位置可以放该数
        {
            if (!st[i]) //没有放数
            {
                path[i] = nums[u];
                st[i] = true;
                dfs(nums, u + 1, u + 1 < nums.size() && nums[u + 1] == nums[u] ? i + 1 : 0);
                //下一个数和当前摆放的数不同，可以选择任意位置；如果相同，必须摆放在该数后面
                st[i] = false; //回溯
            }
        }
    }
};

枚举每个位置可以放哪些数

以该种枚举顺序，我们可得下图递归搜索树，我们可以看出，出现重复方案的原因是因为，当我们在枚举某一位置时，如果我们将两个1看作是不同元素，那么我们枚举时可以选择把哪个1放在该位置上.但是明显放蓝色的1和绿色的1最终的方案都是一样的，因此我们在枚举每个位置可以放哪些数时，如果下一个选择的数和当前选择的数相同，那么我们就跳过。

C ++代码

class Solution {
public:
    vector<vector<int>> res;
    vector<int> path;
    vector<bool> st;
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int n = nums.size();
        path = vector<int> (n);
        st = vector<bool> (n);
        dfs(nums, 0);
        return res;
    }

    void dfs(vector<int>& nums, int u) //u表示枚举到的位置
    {
        if (u == nums.size())
        {
            res.push_back(path);
            return;
        }

        for (int i = 0; i < nums.size(); i ++) //枚举该位置可以放哪些数
        {
            if (!st[i]) 
            {
                path[u] = nums[i];
                st[i] = true;
                dfs(nums, u + 1);
                st[i] = false;
                while (i + 1 < nums.size() && nums[i + 1] == nums[i]) i ++; //跳过相同的数
            }
        }
    }
};

AcWing 94. 递归实现排列型枚举

AcWing上面的两道题是用数组模拟，基本思路与上面一样，这里只贴出枚举顺序为每个位置可以放什么数的代码

C ++代码

#include <iostream>

using namespace std;

const int N = 10;

int n;
int a[N];
bool st[N];

void dfs(int u)
{
    if (u > n)
    {
        for (int i = 1; i <= n; i ++) cout << a[i] << ' ';
        cout << endl;
        return;
    }

    for (int i = 1; i <= n; i ++)
    {
        if (!st[i])
        {
            a[u] = i;
            st[i] = true;
            dfs(u + 1);
            st[i] = false;
        }
    }
}

int main()
{
    cin >> n;
    dfs(1);
    return 0;
}

AcWing 1537. 递归实现排列类型枚举 II

注意：该题目要求字典序输出，所以选择枚举顺序时只能枚举每个位置上可以放什么数

C ++代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 10;

int n;
int a[N];
int path[N];
bool st[N];

void dfs(int u)
{
    if (u >= n)
    {
        for (int i = 0; i < n; i ++) cout << path[i] << ' ';
        cout << endl;
        return;
    }

    for (int i = 0; i < n; i ++)
    {
        if (!st[i])
        {
            path[u] = a[i];
            st[i] = true;
            dfs(u + 1);
            st[i] = false;
            while (i + 1 < n && a[i + 1] == a[i]) i ++;
        }
    }
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++) cin >> a[i];
    sort(a, a + n);
    dfs(0);
    return 0;
}