球盒模型三要素：

1. 小球是否相同
2. 盒子是否相同
3. 是否允许空盒

根据上述三要素，球盒模型一共有8种类型：

1. n个相同小球，m个不同盒子，不允许空盒子 —— n同球，m异盒，无空
2. n个相同小球，m个不同盒子，允许有空盒子 —— n同球，m异盒，可空
3. n个相同小球，m个相同盒子，不允许空盒子 —— n同球，m异盒，无空
4. n个相同小球，m个相同盒子，允许有空盒子 —— n同球，m异盒，可空
5. n个不同小球，m个相同盒子，不允许空盒子 —— n同球，m异盒，无空
6. n个不同小球，m个相同盒子，允许有空盒子 —— n同球，m异盒，可空
7. n个不同小球，m个不同盒子，不允许空盒子 —— n同球，m异盒，无空
8. n个不同小球，m个不同盒子，允许有空盒子 —— n同球，m异盒，可空

其中$n≥m$，即球比盒子多。

球盒模型解决方法

同球异盒

• 5同球，3异盒，无空

隔板法：

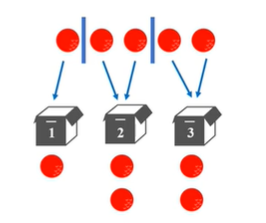
公式：$C_{5-1}^{3-1} = C_4^2 = 6$

解释：5个小球有4个空，插2块板子将小球分成3堆，有6种可能。

• 5同球，3异盒，可空

虚拟球 + 隔板法：有几个盒子，就加几个虚拟球

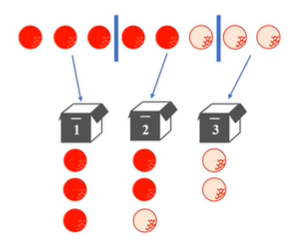
公式：$C_{8-1}^{3-1} = C_7^2 = 21$

同球同盒

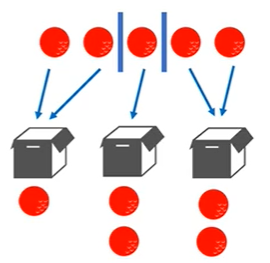
• 5同球，3同盒，无空

使用隔板法，由于盒子相同，会产生重复方案。正确做法是使用正整数拆分的方法：
5 = 1 + 1 + 3 = 1 + 2 + 2，共2种拆分方法，由于盒子相同，所以不用考虑拆分顺序。

• 5同球，3同盒，可空

由于盒子可空，应使用自然数数拆分的方法：
5 = 1 + 1 + 3 = 1 + 2 + 2 = 0 + 0 + 5 = 0 + 1 + 4 = 0 + 2 + 3，共5种拆分方法。

异球同盒

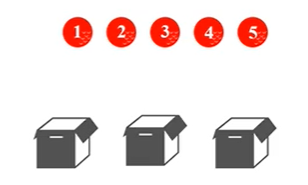
• 5异球，3同盒，无空

因为不允许空盒子，那么5个球放到3个盒子的拆分方案只有2种：
5 = 3 + 1 + 1 = 1 + 2 + 2
因为5个球是不同的，可以分上面两种情况讨论：

1. $C_5^3 × C_2^1 ÷ P_2^2$
2. $C_5^1 × C_4^2 ÷ P_2^2$

情况(1)解释：从5个不同的球中挑出3个放入1个盒子，再从剩下的2个球中挑出1个放入一个盒子。因为盒子相同，且有两个盒子的都是放入1个球，存在重复方案，所以除以$P_2^2$。

情况(2)解释：从5个不同的求中挑出1个放入一个盒子，在从剩下的4个球中挑出2个放入一个盒子，最后剩下两个放入一个盒子。。因为盒子相同，且有两个盒子的都是放入2个球，存在重复方案，所以除以$P_2^2$。

最终方案数为：$C_5^3 × C_2^1 ÷ P_2^2 + C_5^1 × C_4^2 ÷ P_2^2 = 25$

• 5异球，3同盒，可空

因为允许空盒子，那么5个球放到3个盒子的拆分方案只有5种：
5 = 1 + 1 + 3 = 1 + 2 + 2 = 0 + 0 + 5 = 0 + 1 + 4 = 0 + 2 + 3
因为5个球是不同的，可以分上面5种情况讨论：
1. $C_5^3 × C_2^1 ÷ P_2^2$
2. $C_5^1 × C_4^2 ÷ P_2^2$
3. $C_5^5$
4. $C_5^1 × C_4^4$
5. $C_5^2 × C_3^3$

情况(1)、(2)的总方案数已经算过，为25种
情况(3)解释：从5个不同的球中选出5个放入一个盒子，其它盒子放球。
情况(4)解释：从5个不同的球中选出1个放入一个盒子，再选出4个放入一个盒子
情况(5)解释：从5个不同的球中选出2个放入一个盒子，再选出3个放入一个盒子

总方案数： $25 + 1 + 5 + 10 = 41$

异球异盒

• 5异球，3异盒，无空

这个问题可以分两步解决：

1. 第一步，不考虑盒子，先安排球。因为不允许空盒子，那么5个球放到3个盒子的拆分方案只有2种：5 = 3 + 1 + 1 = 1 + 2 + 2，方案数为：$C_5^3 × C_2^1 ÷ P_2^2 + C_5^1 × C_4^2 ÷ P_2^2 = 25$。
2. 第二步，将3个盒子进行排列，方案数为$P_3^3 = 6$。

总方案数为$25 × 6 = 150$。

• 5异球，3异盒，可空

对每个球来说，都有3种可能：

1. 放到1号盒子
2. 放到2号盒子
3. 放到3号盒子

总方案数为$3^5=243$。

总结

根据是否同球、是否同盒、是否可空三要素，球盒模型一共分8种类型，如果设n = 5, m = 3：

1. n个相同小球，m个不同盒子，不允许空盒子 —— n同球，m异盒，无空 —— 隔板法
2. n个相同小球，m个不同盒子，允许有空盒子 —— n同球，m异盒，可空 —— 加入虚拟球的隔板法
3. n个相同小球，m个相同盒子，不允许空盒子 —— n同球，m异盒，无空 ——拆正整数之和
4. n个相同小球，m个相同盒子，允许有空盒子 —— n同球，m异盒，可空 ——拆自然数之和
5. n个不同小球，m个相同盒子，不允许空盒子 —— n同球，m异盒，无空 —— 按拆正整数之和之和的方法分类讨论
6. n个不同小球，m个相同盒子，允许有空盒子 —— n同球，m异盒，可空 —— 按拆自然数之和之和的方法分类讨论
7. n个不同小球，m个不同盒子，不允许空盒子 —— n同球，m异盒，无空 —— 先安排不同的小球，在对盒子进行全排列
8. n个不同小球，m个不同盒子，允许有空盒子 —— n同球，m异盒，可空 —— $m^n$