二叉搜索树的一种吧（我这个感觉）。不是很熟悉哈哈，不过权当笔记了。
看起来很难其实写几遍就简单了（原始数据结构通性）

首先要先学二叉搜索树，应该是挺好理解的。
当情况特殊的时候二叉搜索树就会变成链，没啥效率了。那么Splay就是为了解决这个问题的。

形象点说就是，把看起来很高的二叉搜索树硬生生压扁，但是依旧合法。

结构体和一些函数的定义及含义

struct node{
  int ch[2];//所有儿子，做儿子是大于，右儿子是小于
  int cnt=0;//该值的出现个数 相当于等于
  int ff;//父亲
  int size;//树的大小
  int val;//该节点的值
};
node t[N];平衡树
int root;//根节点
int cnt;//总结点数

下方定义的f,u,z,x分别表示 父节点，起始节点/操作节点（儿子），祖父节点，值

pushup操作

对于下面的操作，必须通过pushup来维护size的正确性,这里记录的size包括该节点自己所以要+1。

int pushup(u){
    return t[u].size=t[t[u].ch[0]].size+t[t[u].ch[1]].size+t[u].cnt;
}

几个有助于码风的小操作

int fa(int u){ return t[u].ff;}
bool son(int f,int x){
    return x>t[f].val;
}

旋转（rotate）

模板，背过即可。

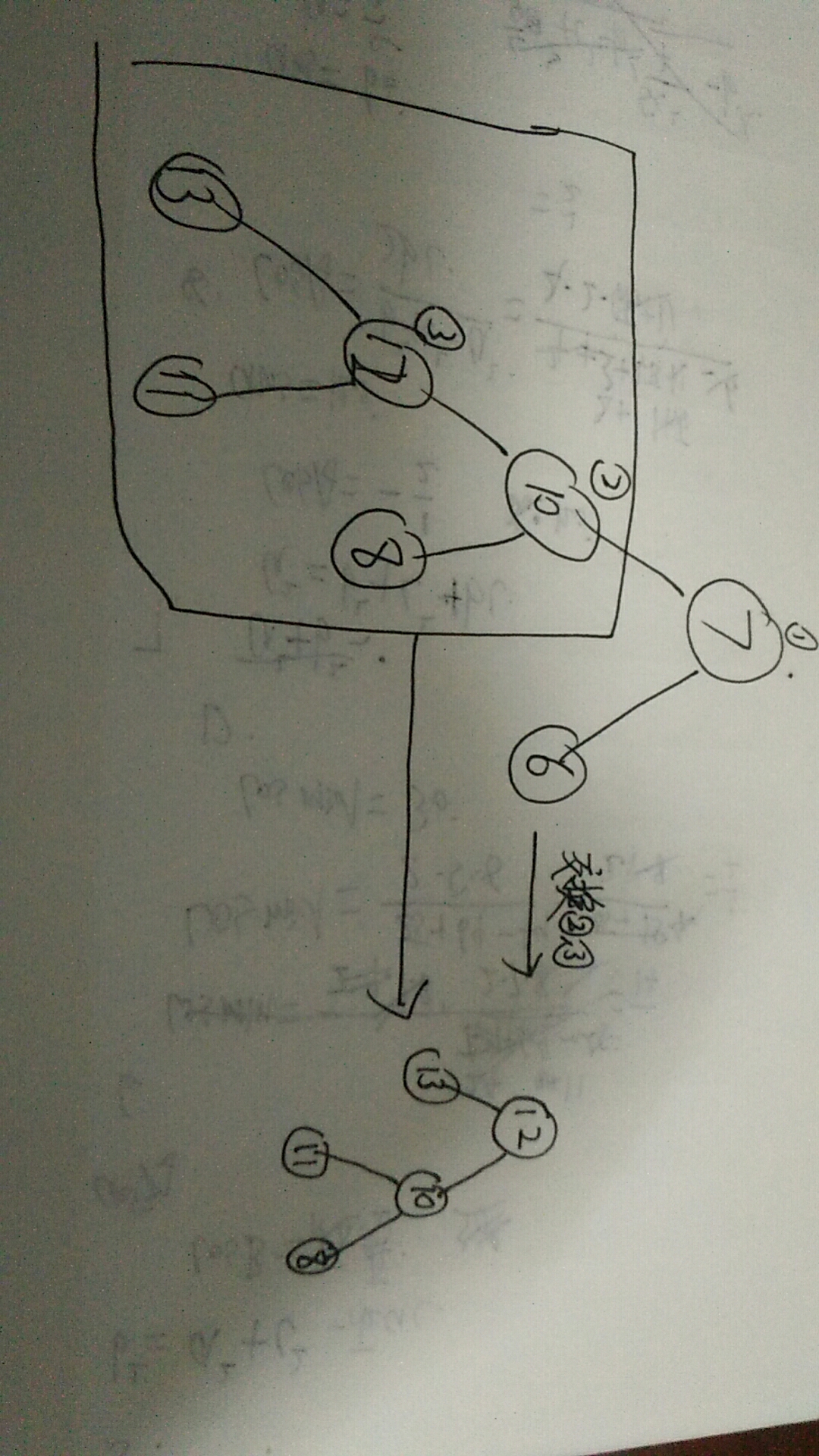
差不多就是这个意思，想要理解可以手动画一画。
第一步是将u替换到f位置，第二步是将u的（u相对于f位置的另一个位置）的儿子替换到u的位置，第三步是将f替换到刚才u的那个儿子的位置.描述的太糟糕了。。

上个代码

 void rotate(int u){
     int f = fa(u);//记录父节点
     int z = fa(f);//记录祖父节点
     int k = t[u].val>t[f].val;//记录u在父节点的左右位置

     t[z].ch[son(z,t[f].val)]=u;t[u].ff=z;
     t[f].ch[k]=t[u].ch[k^1];t[t[u].ch[k^1]].ff=f;
     t[u].ch[k^1]=f;t[f].ff=u;//谋权篡位操作
     pushup(f),pushup(u);//更新size，这个时候父亲是子节点，先更新小的。
 }

splay操作

这个高端操作，如果祖父，父亲和儿子在一条链上，就先交换父亲，否则就先交换儿子。最后再交换儿子。
上代码

void spaly(int u,int goal){//将u旋转为goal节点的儿子
    while(t[u].ff!=goal){//当没有成为goal节点的儿子时
        int f = fa(u),z=fa(f);//记录祖父和父亲
        if(z!=goal)//如果祖父不是目标
        (t[f].ch[0]==u)^(t[z].ch[0]==f)?rotate(u):rotate(f);//判断先交换父亲还是儿子，防止出现链
        rotate(u);//交换一下儿子
    }
    if(goal == 0)root = goal;//维护根节点，因为0号节点等于指针，指向根节点，如果root是0，等于空树。
}

查找（find）

查找操作，查找到将他转到根节点来。当然也可以自己加入是否找到操作。

void find(int x){
    int u = root;//从根节点开始查找
    if(root==0)return;//如果这个数是空树，就返回
    while(t[u].ch[son(t,x)]&&t[u]!=x)u=t[u].ch[son(t,x)];//如果有子节点，并且u的值不是x，就往下走
    splay(u,goal);//将值转到根
}

查找前驱和后继（ha_ne）

先查找x，将节点splay到根节点，如果是前驱，那一定是比x小，所以在右侧，如果是后继，那一定比x大，在左侧。
也就是说如果ope是1则前驱，若0则后继。

int he_ne(int x,bool ope){
    find(x);//先查找到这个点（或者说第一个大于他第一个小于他的节点），将他spaly到根节点
    if(t[root].val<x&&ope)return root;//如果根节点小于他并且是查找前驱，那么返回根节点
    if(t[root].val>x&&!ope)return root];//如果根节点大于他并且是查找后继，那么返回根节点
    if(ope)u=t[root].ch[ope^1];//如果是查找前驱，那在右子树查找，否则在左子树
    while(t[u].ch[ope])u=t[u].ch[ope];//查找左子树的最小值和右子树的最大值即可作为答案。
    return u;
}

插入（insert）

插入节点，如果已经存在，就给节点的计数器++。
如果没有就一直往下跑，直到创建新节点。

void insert(int x){
    int u = root;int f = 0;//从根节点开始找，并随时更新父节点。
    while(u&&t[u].val!=x){
        f=u;
        u=t[u].ch[x>t[u].val];
    }
    if(t[u].cnt)t[u].cnt++;//如果已经存在这个值，只需要计数++即可
    else {//不然创建新节点
        u=++cnt;
        if(f)t[f].ch[x>t[f].val]=u;//不能给指针创建左右儿子，特判一下。
        t[u].val=x;
        t[u].ff=f;
        t[u].cnt=1;
        t[u].size=1;
    }
    splay(u,0);
}

删除操作（delt）

这个基本不怎么用吧。（ε=ε=ε=┏(゜ロ゜;)┛
查找x的前驱和后继，让前驱splay到根节点，后继splay到前驱，那么x一定是后继右儿子，并且是叶节点没有子树。毕竟紧挨着的三个值。
可以用（3，4，5）来画图思考，5一定是3的左儿子，4一定是5的右儿子，不存在任何值能左4的儿子。因为这个值一定被分配到了前驱的右儿子或者后继的左儿子。
如果cnt大于1，就–。如果等于一，直接把这个节点舍弃掉。

void delt(int x){
    int pre=he_ne(x,1);//查找前驱
    int nex=he_ne(x,0);//查找后继
    splay(pre,0);splay(nex,pre);//将前驱作为根节点，后继以前驱为父节点
    int u = t[nex].ch[0];//u一定是后继的右儿子
    if(t[u].cnt>1)t[u].cnt--,splay(u,0);//如果存在这个值，并且大于1个，那就--
    else t[nex].ch[0]=0;否则直接删除这个节点。
}

学习源：
yyb
yzhang
如果有错误，欢迎指出。谢谢🙇‍