对于SPFA算法来说, 某个点加入一次队列, 该点到源点的最短距离就更新了一次, 当加入k次, 路径边数为k的最短路径就确定了。
SPFA求负环问题只能用循环队列原因
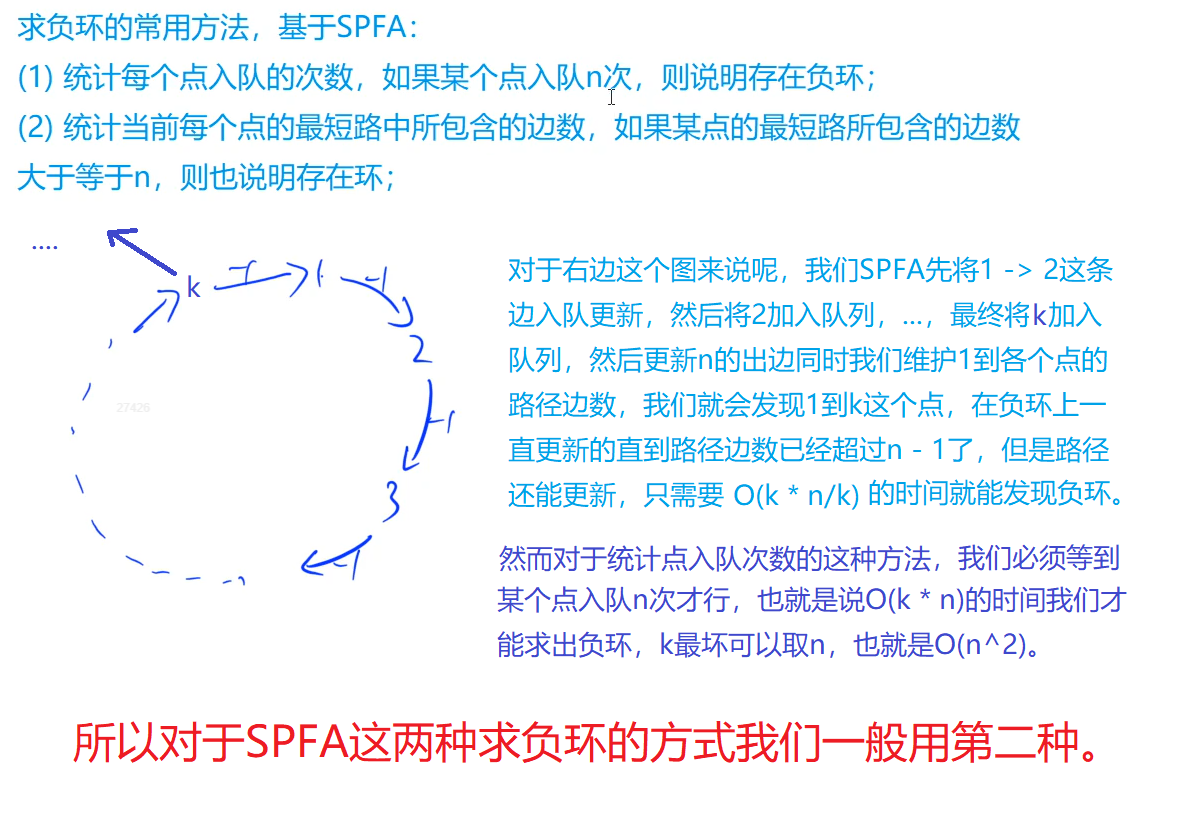
由于SPFA求负环的时间复杂度趋近O(nm), 很有可能负环还没求出来, 就超时了。例题
所以我们这里有两个解决方法:
1.可以维护所有点的入队次数x, 当x大于某个阈值的时候, 就有负环了。(玄学)
这时我们可以将有负环的条件设置为:
当所有点的入队的次数超过 kn(k的值就靠试, 从2开始一个一个的试, 哪个能ac, k就是那个值) 时,
我们就认为图中很大可能存在负环。 acwing 单词环
2.将spfa的队列换成栈(稳妥) -> 只在求负环的时候会快, 只求最短路时不要轻易替换 例题
搜索的顺序可能影响找到负环的快慢
spfa用栈的原因: 最短路:队列当你出队时你已经被更新到了当前最小值了, 而栈的话你一进栈马上就出来了, 这样的话, 如果该点被更新多次那么它就要更新其出边多次, 就很慢, 求负环由于算的是更新次数, 所以自然某个点更新的次数累计越多越好。由于栈是进了马上出, 所以不存在说点数累积的情况, 自然也就不需要用循环栈了。
01分数规划问题(求一堆数的和/另一堆数的和的最值问题(数的个数一样可以被消掉)。可以与最短路, 最小生成树, 负环等图论问题结合)
在图论问题中我们求一堆的和除以另一堆的和最大值的问题
解决方案: 二分
模板题
题目实例
01分数规划问题解题步骤总结

