堆相关知识复习(y总版)

我们本次预计使用Java来实现一个链式的大根堆，支持插入节点，修改节点值，堆排序，打印堆结构等功能。并将项目打包为jar包在cmd控制台运行。

1.功能设计

大根堆是一个完全二叉树，每个父节点的值大于两个子节点的值，那么要实现插入节点的操作，我们就需要知道从根节点插入所要经过的路径，以在节点5插入为例：

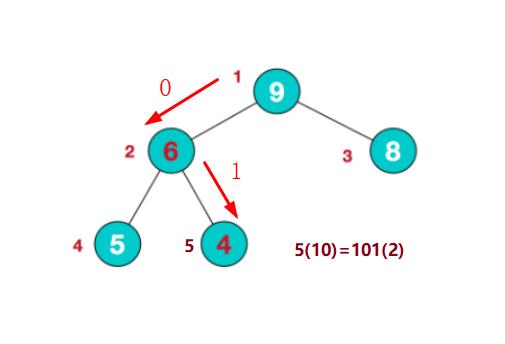
5的二进制表示为101，第一个1代表从根节点1开始，第二个0表示向左儿子走，第三个1表示向右儿子走，最终走到了节点5这里。这个找到插入节点路径的函数用getPath(x)实现。

数据结构设计

我们的每个堆中包括一个堆容量$siz$、堆二叉树$**head$、数组$sortedArray$用于存储堆排序结果
每个堆二叉树节点包括节点值$val$，左右儿子编号$left$、$right$，父亲节点编号**$fa$
为了能够较为直观地打印出树，编写一个DefaultBinaryTreeNodePrinter和DefaultBinaryTreePrinter类用于树的打印。

堆排序，操作简单来讲就是将堆顶的元素拿出来，之后找到堆最后的一个元素的值$getPath(堆的大小)$，用其替换堆顶元素的值，之后从堆顶开始执行下沉操作$down()$，同时堆大小$siz-1$,循环往复直到堆大小siz=0。

将排序好的结果存入数组$sortedArray$。

我们的堆支持一下几种操作：

• 0: 堆初始化
• 1: 堆中插入一个元素
• 2: 修改堆节点v的元素值为k
• 3: 堆排序操作
• 4: 打印堆的树结构
• 5: 打印堆排序结果
• 6: 输入一个数组构建堆
• 9: 退出程序

2.代码实现

先上C++代码(没有操作6和画树操作)：

#include<bits/stdc++.h>
using namespace std;
struct node{
    int val;
    node *left;
    node *right;
    node *fa;

    node(int x): val(x),left(NULL),right(NULL),fa(NULL) {};
    node(int x,node *fa):val(x),left(NULL),right(NULL),fa(fa) {};
};
struct Heap{
    int siz;
    node *head;
    vector<int> sortedArray;

    string getPath(int t)
    {
        string s="";
        while(t!=1)
        {
            int k=t%2;
            s=(char)(k+'0')+s;
            t/=2;
        }
        return s;
    }


    void up(node *root,string s,int idx)
    {
        if(idx==s.size()){
            if(root->val>root->fa->val)
            {
                swap(root->val,root->fa->val);
            }   
            return ;
        } 
        if(s[idx]=='1'){
            up(root->right,s,idx+1); 
            if(root->fa){
                if(root->val>root->fa->val) swap(root->val,root->fa->val);
            }
        }
        else{
            up(root->left,s,idx+1);
            if(root->fa){
                if(root->val>root->fa->val) swap(root->val,root->fa->val);
            }
        }

    }

    void insert(int x){
        if(!siz){
            head=new node(x);
            siz++;
        }
        else{
            string s=getPath(siz+1);
            head=insert(head,NULL,s,0,x);
            siz++;
            s=getPath(siz);
            up(head,s,0);
        }
    }

    node* insert(node *root,node *pre,string s,int idx,int x)
    {
        if(!root){
            return new node(x,pre);
        } 
        if(s[idx]=='1'){
            root->right=insert(root->right,root,s,idx+1,x);   
        }
        else{
            root->left=insert(root->left,root,s,idx+1,x);
        }
        return root;
    }

    node* modify(node *root,string s,int idx,int x)
    {
        if(idx==s.size()){
            if(x < root->val){
                puts("Value k < key value!");
                return root;
            }

            root->val=x;
            return root;                 
        } 
        if(s[idx]=='1'){
            root->right=modify(root->right,s,idx+1,x);   
        }
        else{
            root->left=modify(root->left,s,idx+1,x);
        }
        return root;
    }

    void increaseKey(int v,int k)
    {
        if(v>siz)
        {
            puts("Node v not exist!");
            return ;
        }
        else{
            string s=getPath(v);
            head=modify(head,s,0,k);
            down(v,head,siz);
            up(head,s,0);
        }

    }

    node *copyHeap(node *a,node *b)
    {
        if(b)
            a=new node(b->val,b->fa);
        else 
            return NULL;
        a->left=copyHeap(a->left,b->left);
        a->right=copyHeap(a->right,b->right);
        return a;
    }

    int query(node *root,string s,int idx)
    {
        if(idx==s.size()){
            return root->val;                 
        } 

        if(s[idx]=='1'){
            return query(root->right,s,idx+1);   
        }
        else{
            return query(root->left,s,idx+1);
        }
    }

    node *queryNode(node *root,string s,int idx)
    {
        if(idx==s.size()){
            return root;                 
        } 

        if(s[idx]=='1'){
            return queryNode(root->right,s,idx+1);   
        }
        else{
            return queryNode(root->left,s,idx+1);
        }
    }
    //下沉操作
    void down(int x,node *root,int len)
    {
        //找到左右儿子中最大的数，替换父亲节点的值
        int t=x;
        if(x*2<=len && query(root,getPath(2*x),0)>query(root,getPath(t),0)) t=2*x;
        if(x*2+1<=len && query(root,getPath(2*x+1),0)>query(root,getPath(t),0)) t=2*x+1;
        if(x!=t)
        {
            node *a=queryNode(root,getPath(x),0);
            node *b=queryNode(root,getPath(t),0);
            swap(a->val,b->val);
            down(t,root,len);
        }

    }

    void output(node *root)
    {
        queue<node*> q;
        q.push(root);
        while(q.size())
        {
            int len=q.size();
            for(int i=0;i<len;i++)
            {
                auto t=q.front(); q.pop();
                if(t->left) q.push(t->left);
                if(t->right) q.push(t->right);
                cout<<t->val<<" ";
            }
            puts("");
        }
    }

    void outputSortResult()
    {
        reverse(sortedArray.begin(),sortedArray.end());
        for(auto x:sortedArray) cout<<x<<" ";
        puts("");
    }

    void heapSort(Heap hp)
    {
        sortedArray.clear();
        Heap temp;
        temp.siz=hp.siz;
        temp.head=copyHeap(temp.head,hp.head);
        queue<node*> q;
        q.push(temp.head);
        //output(temp.head);
        for(int i=0;i<siz;i++)
        {
            sortedArray.push_back(temp.head->val);
            string s=getPath(temp.siz--);
            temp.head->val=query(temp.head,s,0);
            //int val=query(siz)->val;
            //cout<<temp.head->val<<endl;
            down(1,temp.head,temp.siz);
            //output(temp.head);
        }

    }

    Heap():siz(0){}

};
int main()
{
    Heap h;
    h.insert(5);
    h.insert(6);
    h.insert(7);
    h.insert(1);
    h.insert(2);
    h.increaseKey(4,10);
    h.output(h.head);
    h.heapSort(h);
    h.outputSortResult();
    h.insert(15);
    h.insert(25);
    h.insert(36);
    h.heapSort(h);
    h.outputSortResult();

    return 0;
}

Java代码另取

项目运行测试结果：

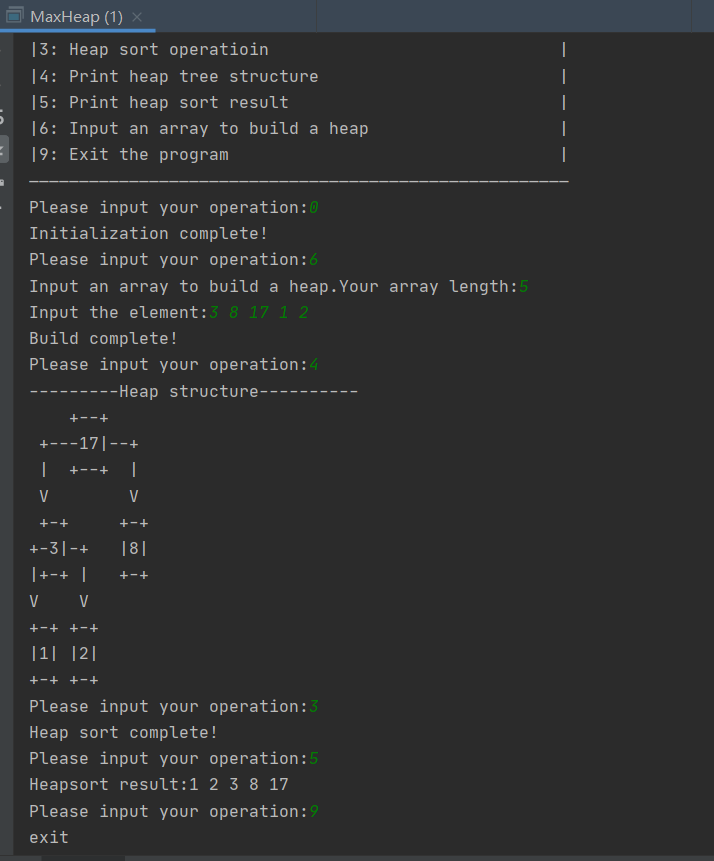
3.Maven项目导出jar包

我们新建一个Maven项目

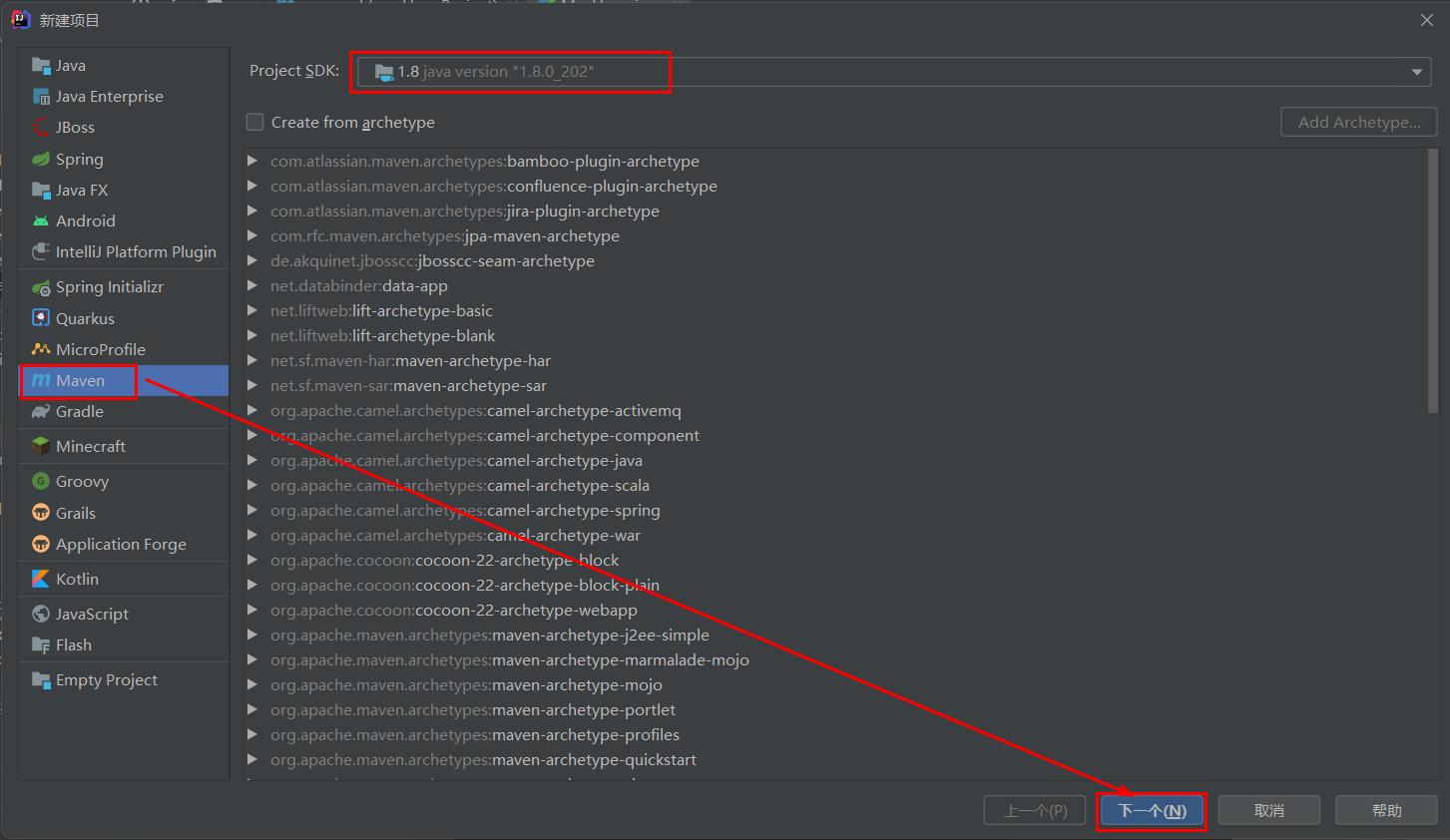
之后找到项目的pom文件，输入一个maven-plugin-shade的启动依赖。

maven-plugin-shade必须和Maven构建生命周期中的package阶段绑定，也就是说，当执行mvn package时会自动触发shade。

我们的项目主类的路径为com.joy187.MaxHeap：

pom.xml

<?xml version="1.0" encoding="UTF-8"?>
<project xmlns="http://maven.apache.org/POM/4.0.0"
         xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
         xsi:schemaLocation="http://maven.apache.org/POM/4.0.0 http://maven.apache.org/xsd/maven-4.0.0.xsd">
    <modelVersion>4.0.0</modelVersion>

    <groupId>org.example</groupId>
    <artifactId>maxHeapProject</artifactId>
    <version>1.0-SNAPSHOT</version>

    <build>
        <plugins>
            <plugin>
                <groupId>org.apache.maven.plugins</groupId>
                <artifactId>maven-shade-plugin</artifactId>
                <version>3.2.4</version>
                <configuration>
                    <transformers>
                        <transformer
                                implementation="org.apache.maven.plugins.shade.resource.ManifestResourceTransformer">
                            <!--你的项目主类名称-->
                            <mainClass>com.joy187.MaxHeap</mainClass>
                        </transformer>
                    </transformers>
                </configuration>
                <executions>
                    <execution>
                        <phase>package</phase>
                        <goals>
                            <goal>shade</goal>
                        </goals>
                    </execution>
                </executions>
            </plugin>
        </plugins>
    </build>
</project>

刷新Maven项目后找到package并点击，进行打包操作

打包完成出现success字样：

4.cmd控制台运行项目

项目构建好后，我们找到target文件夹，里面不带有original的就是我们的可执行jar包了：

在该文件夹中输入cmd进入控制台：

控制台输入指令：

java -jar 项目名称.jar

之后就可以运行项目了！