一、LRU和LFU算法
LRU算法
LRU Least Recently Used 最近最少使用算法
LRU 算法的思想是如果一个数据在最近一段时间没有被访问到,那么在将来它被访问的可能性也很小。所以,当指定的空间已存满数据时,应当把最久没有被访问到的数据淘汰。
也就是淘汰数据的时候,只看数据在缓存里面待的时间长短这个维度。
这样子做有什么缺点呢?我们来看个例子
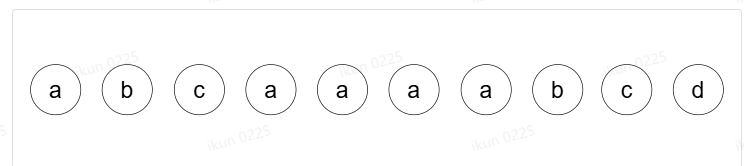
按照LRU算法进行访问和数据淘汰,10次访问的结果如下图所示
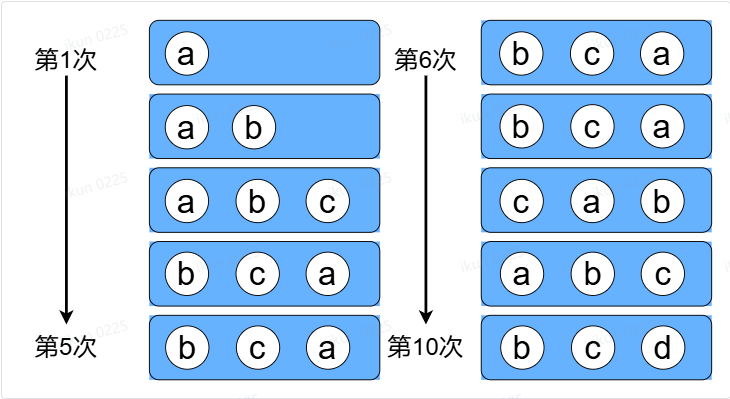
10次访问结束后,缓存中剩下的数据是b、c、d三个元素,这个显然不太合理。
直观上讲,为什么说他不合理,是因为明明a是被频繁访问的数据,最终却被淘汰掉了。所以如果要改进这个算法,我们希望的是能够记录每个元素的访问频率信息,访问频率最低的那个才是最应该被淘汰的那个。
恭喜你,这就是LFU的规则。
在开始LFU之前,我们先来看一下LRU的代码怎么写。
有句古话讲得好:缓存就是Map + 淘汰策略。Map的作用是提供快速访问,淘汰策略是缓存算法的灵魂,决定了命中率的高低。根据对于LRU的描述,我们需要一个东西(术语叫做数据结构)来记录数据被访问的先后顺序,这里我们可以选择链表。
打开IDE,迅速写下第一行代码:
type LRU struct {
data map[string]*list.Element
cap int
list *list.List
}
解释一下为什么需要这几个变量, cap 是缓存中可以存放的数据个数,也就是缓存的容量上限。data就是Map。List我们用来记录数据的先后访问顺序,每次访问,都把本次访问的节点移动到链表中的头部。这样子整个链表就会按照近期的访问记录来排序了。
func (lru *LRU) add(k, v string) {
if Map中存有这条Key {
替换Map中的Value值
将链表中的对应节点移到最前面
} else {
if 已经达到缓存容量上限 {
获取链表尾部节点的Key,并从Map中删除
移除链表尾部的Node
}
创建要插入的新节点
将新节点插入到链表头部
放入Map中
}
}
func (lru *LRU) get(k string) string {
if Map中存有这条Key {
返回查询到的Value
将对应节点移动到链表头部
} else {
返回 空
}
}
LFU算法
我们已经成功的写出了LRU算法(伪代码),接下来尝试自己写一下LFU算法。首先我们知道LFU算法比LRU多了什么,LFU需要记录每条数据的访问次数信息,并且按照访问次数从高到低排序,访问次数用什么来记录呢?
只需要在链表节点中增加一个访问频率Frequency,就可以了,这个Frequency可以使用int来存储。同时排序的规则稍加变动,不是把最近访问的放到最前面,而是按照访问频率插入到对应位置即可。如果频率相同,再按照LRU的规则,比较谁是最新访问的。
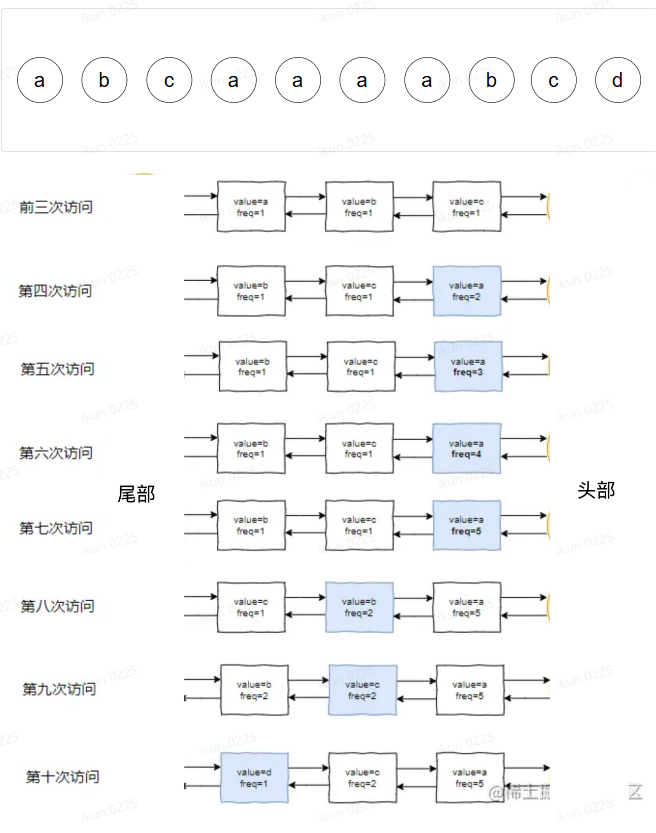
总结:
讲完了LRU和LFU,我们来看一下他们有啥优缺点。
LRU
优点:实现简单、可以很快的适应访问模式的改变
缺点:对于热点数据的命中率可能不如LFU
LFU
优点:对于热点数据命中率更高
缺点:难以应对突发的稀疏流量、可能存在旧数据长期不被淘汰,会影响某些场景下的命中率(如外卖),需要额外消耗来记录和更新访问频率
二、TinyLFU
Count-Min Sketch 算法
刚才提到了LFU需要统计每个条数据的访问频率,这就需要一个int或者long类型来存储次数,但是仔细一想,一条缓存数据的访问次数真的需要int类型这么大的表示范围来统计吗?我们认为一个缓存被访问15次已经算是很高的频率了,那么我们只用4个Bit就可以保存这个数据。(2^4=16)
再来介绍一个cmSketch算法,看过硬核课堂BloomFilter视频的都知道,BloomFilter利用位图的思想来标记一条数据是否存在,存在与否可以用某个Bit位的0 | 1来代替,那么我们能不能扩展一下,利用这种思想来计数呢?
我们给要计数的值计算一个Hash,然后在位图中给这个Hash值对应的位置累加1就可以了,但是BloomFilter中的一个典型问题是假阳性,可以说只要是用Hash计算就有存在冲突的可能,那么cmSketch计数法如果出现冲突会怎么样呢?会给同一个位置多计算访问次数。这里cmSketch选择了以最小的统计数据值作为结果。这是一个不那么精确地统计方法,但是可以大致的反应访问分布的规律。
因为这个算法也就有了一个名字,叫做Count-Min Sketch。
下面我们来手撕这个算法。
//根据BloomFilter来思考一下我们需要什么
//一个bit图,n个Hash函数
//一个BitMap的实现
type cmRow []byte //byte = uint8 = 0000,0000 = COUNTER 4BIT = 2 counter
//64 counter
//1 uint8 = 2counter
//32 uint8 = 64 counter
func newCmRow(numCounters int64) cmRow {
return make(cmRow, numCounters/2)
}
func (r cmRow) get(n uint64) byte {
return byte(r[n/2]>>((n&1)*4)) & 0x0f
}
0000,0000|0000,0000| 0000,0000 make([]byte, 3) = 6 counter
func (r cmRow) increment(n uint64) {
//定位到第i个Counter
i := n / 2 //r[i]
//右移距离,偶数为0,奇数为4
s := (n & 1) * 4
//取前4Bit还是后4Bit
v := (r[i] >> s) & 0x0f //0000, 1111
//没有超出最大计数时,计数+1
if v < 15 {
r[i] += 1 << s
}
}
//cmRow 100,
//保鲜
func (r cmRow) reset() {
// 计数减半
for i := range r {
r[i] = (r[i] >> 1) & 0x77 //0111,0111
}
}
func (r cmRow) clear() {
// 清空计数
for i := range r {
r[i] = 0
}
}
//快速计算最接近x的二次幂的算法
//比如x=5,返回8
//x = 110,返回128
//2^n
//1000000 (n个0)
//01111111(n个1) + 1
// x = 1001010 = 1111111 + 1 =10000000
func next2Power(x int64) int64 {
x--
x |= x >> 1
x |= x >> 2
x |= x >> 4
x |= x >> 8
x |= x >> 16
x |= x >> 32
x++
return x
}
如果我们要给n个数据计数,那么每4Bit当做一个计数器Counter,我们一共需要几个uint8来计数呢?答案是n/2
| 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 |
|---|---|---|---|---|---|---|---|
| 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 |
| 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 |
| 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 | 0000 |
//cmSketch封装
const cmDepth = 4
type cmSketch struct {
rows [cmDepth]cmRow
seed [cmDepth]uint64
mask uint64
}
//numCounter - 1 = next2Power() = 0111111(n个1)
//0000,0000|0000,0000|0000,0000
//0000,0000|0000,0000|0000,0000
//0000,0000|0000,0000|0000,0000
//0000,0000|0000,0000|0000,0000
func newCmSketch(numCounters int64) *cmSketch {
if numCounters == 0 {
panic("cmSketch: bad numCounters")
}
numCounters = next2Power(numCounters)
sketch := &cmSketch{mask: uint64(numCounters - 1)}
// Initialize rows of counters and seeds.
source := rand.New(rand.NewSource(time.Now().UnixNano()))
for i := 0; i < cmDepth; i++ {
sketch.seed[i] = source.Uint64()
sketch.rows[i] = newCmRow(numCounters)
}
return sketch
}
func (s *cmSketch) Increment(hashed uint64) {
for i := range s.rows {
s.rows[i].increment((hashed ^ s.seed[i]) & s.mask)
}
}
// 找到最小的计数值
func (s *cmSketch) Estimate(hashed uint64) int64 {
min := byte(255)
for i := range s.rows {
val := s.rows[i].get((hashed ^ s.seed[i]) & s.mask)
if val < min {
min = val
}
}
return int64(min)
}
// 让所有计数器都减半,保鲜机制
func (s *cmSketch) Reset() {
for _, r := range s.rows {
r.reset()
}
}
// 清空所有计数器
func (s *cmSketch) Clear() {
for _, r := range s.rows {
r.clear()
}
}
TinyLFU解决了LFU统计的内存消耗问题,和缓存保鲜的问题,但是TinyLFU是否还有缺点呢?
有,论文中是这么描述的,根据实测TinyLFU应对突发的稀疏流量时表现不佳。大概思考一下也可以得知,这些稀疏流量的访问频次不足以让他们在LFU缓存中占据位置,很快就又被淘汰了。
我们回顾之前讲过的,LRU对于稀疏流量效果很好,那可以不可以把LRU和LFU结合一下呢?就出现了下面这种缓存策略。
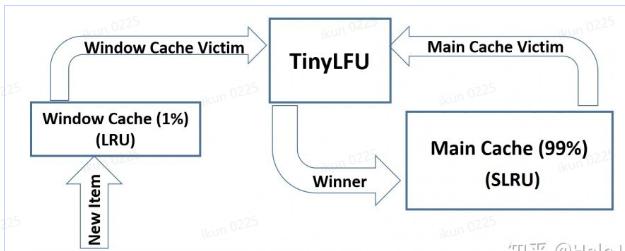
三、Window-TinyLFU
Window-TinyLFU策略里包含LRU和LFU两部分,前端的小LRU叫做Window LRU,它的容量只占据1%的总空间,它的目的就是用来存放短期的突发访问数据。存放主要元素的Segmented LRU(SLRU)是一种LRU的改进,主要把在一个时间窗口内命中至少2次的记录和命中1次的单独存放,这样就可以把短期内较频繁的缓存元素区分开来。具体做法上,SLRU包含2个固定尺寸的LRU,一个叫Probation段A1,一个叫Protection段A2。新记录总是插入到A1中,当A1的记录被再次访问,就把它移到A2,当A2满了需要驱逐记录时,会把驱逐记录插入到A1中。W-TinyLFU中,SLRU有80%空间被分配给A2段。
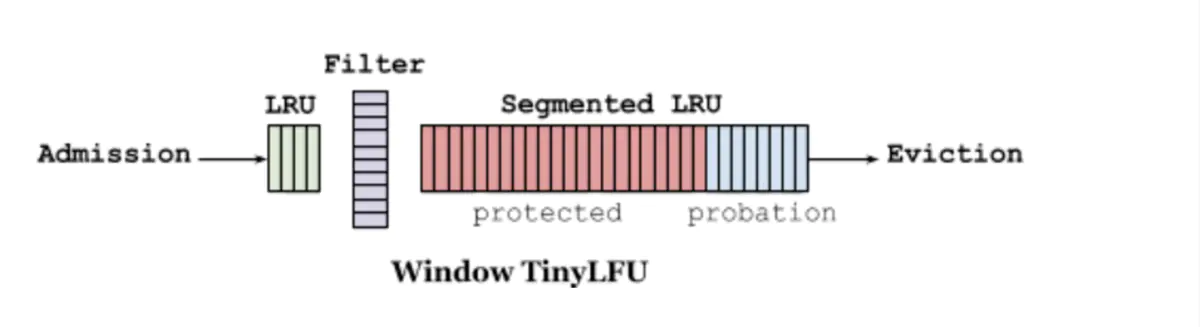
/*
Cache 结构体代表一个缓存系统,该系统采用多种缓存策略和技术来优化存储和检索效率。
它结合了限长缓存(window LRU),分段 LRU(segmented LRU),布隆过滤器(Bloom Filter)
以及计数迷你缩略图(count-min sketch)等多种方法来管理缓存数据。
缓存策略:
如果需要淘汰的时候,需要判断是否出现过,bloom,出现过才能往slu放,只访问一次的也就是说,如果一个数据来了一次,在win被淘汰,如果slru满了,
如果w满了,slu也满了,但是这个数据没出现过,会导致w中的直接淘汰了,但是此时bloom会有计数。如果下一次又进入Iru,又被淘汰,就会进入probation
综上
如果只出现一次,会在window-lru被淘汰。
如果突发性的频繁访问,可能会保留在window-lru,或者进入slru的`probation`区,并经过保活机制。
如果热点数据,肯定会进入slru的protected区。
*/
type Cache struct {
// m 用于同步访问缓存数据,确保并发安全。
m sync.RWMutex
// lru 作为短时高频数据的缓存策略,windowLRU 是一种基于滑动窗口的 LRU 缓存策略。
lru *windowLRU
// slru 用于存储较长时间未被访问的数据,segmentedLRU 是一种分段的 LRU 缓存策略,
// 它可以更有效地管理大量缓存数据。
slru *segmentedLRU
// door 用作快速判断某数据是否存在,使用布隆过滤器可以快速判断某数据是否存在缓存中,
// 但可能会有误判。
door *BloomFilter
// c 用于估计大量数据的频次,count-min sketch 是一种概率数据结构,用于估计数据流中
// 各项的频次。
c *cmSketch
// t 用于调整缓存策略的灵敏度,是一个动态调整的阈值。
t int32
// threshold 用于区分数据是否应该从 lru 晋级到 slru,确保高频数据能够被快速访问。
threshold int32
// data 用于存储具体的缓存数据,键是数据的唯一标识,值是双向链表的元素,
// 这样可以在 O(1) 的时间复杂度内访问和移除数据。
data map[uint64]*list.Element
}
type Options struct {
lruPct uint8
}
// NewCache size 指的是要缓存的数据个数
// NewCache 创建并返回一个新的缓存实例。
func NewCache(size int) *Cache {
// 定义 window 部分缓存所占百分比,这里定义为1%
const lruPct = 1
// 计算出来 widow 部分的容量
lruSz := (lruPct * size) / 100
// 确保 lruSz 至少为1
if lruSz < 1 {
lruSz = 1
}
// 计算 LFU 部分的缓存容量
slruSz := int(float64(size) * ((100 - lruPct) / 100.0))
// 确保 slruSz 至少为1
if slruSz < 1 {
slruSz = 1
}
// LFU 分为两部分,stageOne 部分占比20%
slruO := int(0.2 * float64(slruSz))
// 确保 stageOne 部分至少为1
if slruO < 1 {
slruO = 1
}
// 初始化缓存数据结构
data := make(map[uint64]*list.Element, size)
// 创建并返回缓存实例
return &Cache{
lru: newWindowLRU(lruSz, data),
slru: newSLRU(data, slruO, slruSz-slruO),
door: newFilter(size, 0.01), // 布隆过滤器设置误差率为0.01
c: newCmSketch(int64(size)),
data: data, // 共用同一个 map 存储数据
}
}
func (c *Cache) Set(key interface{}, value interface{}) bool {
c.m.Lock()
defer c.m.Unlock()
return c.set(key, value)
}
func (c *Cache) set(key, value interface{}) bool {
// keyHash 用来快速定位,conflict 用来判断冲突
keyHash, conflictHash := c.keyToHash(key)
// 刚放进去的缓存都先放到 window lru 中,所以 stage = 0
i := storeItem{
stage: 0,
key: keyHash,
conflict: conflictHash,
value: value,
}
// 如果 window 已满,要返回被淘汰的数据
eItem, evicted := c.lru.add(i)
if !evicted {
return true
}
// 如果 window 中有被淘汰的数据,会走到这里
// 需要从 LFU 的 stageOne 部分找到一个淘汰者
// 二者进行 PK
victim := c.slru.victim()
// 走到这里是因为 LFU 未满,那么 window lru 的淘汰数据,可以进入 stageOne
if victim == nil {
c.slru.add(eItem)
return true
}
// 这里进行 PK,必须在 bloomfilter 中出现过一次,才允许 PK
// 在 bf 中出现,说明访问频率 >= 2
if !c.door.Allow(uint32(eItem.key)) {
return true
}
// 估算 windowlru 和 LFU 中淘汰数据,历史访问频次
// 访问频率高的,被认为更有资格留下来
vcount := c.c.Estimate(victim.key)
ocount := c.c.Estimate(eItem.key)
if ocount < vcount {
return true
}
// 留下来的人进入 stageOne
c.slru.add(eItem)
return true
}
// Get 从缓存中获取与指定键关联的值。
// 该方法使用读锁来确保在读取缓存时不会被写操作阻塞,
// 同时也保证了并发访问时的数据安全。
// 参数:
//
// key - 用于检索值的键。类型为interface{},使得可以支持多种类型的键。
//
// 返回值:
// - 接口类型的值,对应于提供的键;如果键不存在,则返回nil。
// - bool 类型的值,表示是否成功找到了与键关联的值。
func (c *Cache) Get(key interface{}) (interface{}, bool) {
// 加读锁
c.m.RLock()
defer c.m.RUnlock()
return c.get(key)
}
// get 从缓存中获取与指定键关联的值。
// 它首先检查键是否存在,如果不存在,则返回nil和false。
// 如果键存在,它会检查是否存在冲突,并相应地更新缓存状态。
//
// 如果成功检索到值,则返回true;如果键不存在或有冲突,则返回false。
func (c *Cache) get(key interface{}) (interface{}, bool) {
// 增加操作计数器
c.t++
// 检查是否达到阈值,达到则重置缓存状态
if c.t == c.threshold {
c.c.Reset()
c.door.reset()
c.t = 0
}
// 将键转换为哈希值,用于缓存查找
keyHash, conflictHash := c.keyToHash(key)
// 尝试从缓存中获取键对应的值
val, ok := c.data[keyHash]
if !ok {
// 如果键不存在,允许对该哈希进行访问,并增加计数
c.door.Allow(uint32(keyHash))
c.c.Increment(keyHash)
return nil, false
}
// 获取存储项的详细信息
item := val.Value.(*storeItem)
// 检查是否存在冲突,如果存在,则不允许访问
if item.conflict != conflictHash {
c.door.Allow(uint32(keyHash))
c.c.Increment(keyHash)
return nil, false
}
// 允许对该哈希进行访问,并增加计数
c.door.Allow(uint32(keyHash))
c.c.Increment(item.key)
// 获取与键关联的值
v := item.value
// 根据项的状态,更新LRU或SLRU缓存状态
if item.stage == 0 {
c.lru.get(val)
} else {
c.slru.get(val)
}
// 返回与键关联的值和成功标志
return v, true
}
func (c *Cache) Del(key interface{}) (interface{}, bool) {
c.m.Lock()
defer c.m.Unlock()
return c.del(key)
}
// del 从缓存中删除指定键的条目。
// 它接受一个键作为输入参数,并返回被删除项的冲突哈希值(如果有的话)以及一个布尔值,表示删除是否成功。
func (c *Cache) del(key interface{}) (interface{}, bool) {
// 将键转换为哈希值,同时检查是否存在哈希冲突。
keyHash, conflictHash := c.keyToHash(key)
// 尝试从缓存数据中获取与键关联的值。
val, ok := c.data[keyHash]
if !ok {
// 如果键不存在于缓存中,则返回失败。
return 0, false
}
// 获取存储项的具体值。
item := val.Value.(*storeItem)
// 检查冲突哈希值是否匹配,如果不匹配,则返回失败。
if conflictHash != 0 && (conflictHash != item.conflict) {
return 0, false
}
// 从缓存中删除键。
delete(c.data, keyHash)
// 返回被删除项的冲突哈希值(如果有的话)以及表示删除成功的布尔值。
return item.conflict, true
}
// keyToHash 根据给定的键生成一个哈希值对。
// 键可以是多种类型,包括nil、uint64、string、[]byte、byte、int、int32、uint32、int64。
// 如果键的类型不受支持,将触发panic。
func (c *Cache) keyToHash(key interface{}) (uint64, uint64) {
// 如果键是nil,返回0, 0。
if key == nil {
return 0, 0
}
// 根据键的类型,选择合适的哈希方法。
switch k := key.(type) {
case uint64:
// 如果键是uint64类型,直接返回键值和0。
return k, 0
case string:
// 如果键是string类型,使用两种不同的哈希方法计算哈希值。
return MemHashString(k), xxhash.Sum64String(k)
case []byte:
// 如果键是[]byte类型,使用两种不同的哈希方法计算哈希值。
return MemHash(k), xxhash.Sum64(k)
case byte:
// 如果键是byte类型,转换为uint64并返回。
return uint64(k), 0
case int:
// 如果键是int类型,转换为uint64并返回。
return uint64(k), 0
case int32:
// 如果键是int32类型,转换为uint64并返回。
return uint64(k), 0
case uint32:
// 如果键是uint32类型,转换为uint64并返回。
return uint64(k), 0
case int64:
// 如果键是int64类型,转换为uint64并返回。
return uint64(k), 0
default:
// 如果键的类型不受支持,触发panic。
panic("Key type not supported")
}
}

