1.并查集
在一些有N个元素的集合问题中,我们通常是在开始让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。然而可以知道,这样空间时间复杂度极高,无法通过题目的时限,这个时候,就可以用到并查集来解答。
并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题。
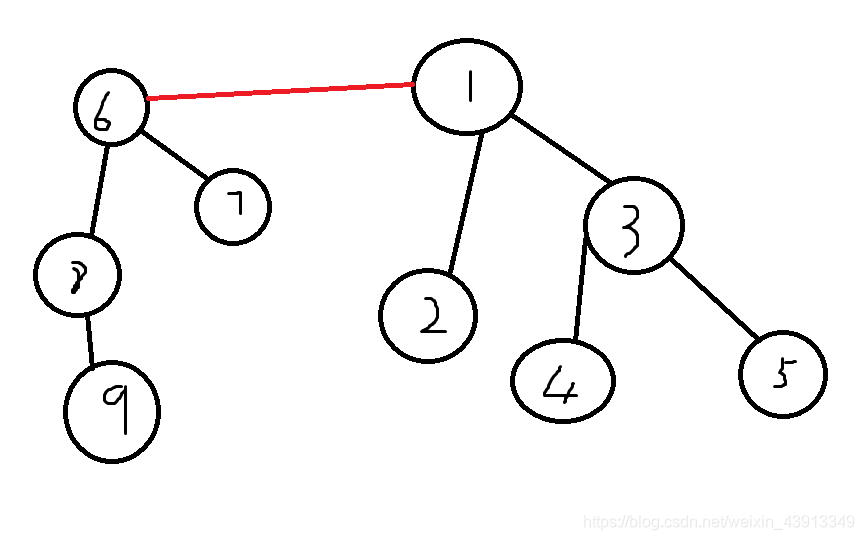
2.初始化
初始化很简单,将每个点所在集合初始化为它自己。如有n个点,就将数组fa[i]=i
void init(){
for(int i=1;i<=n;i++){
fa[i]=i;
}
}
3.查找
这一步,我们只需要找到根节点,即元素所在的集合。就是当fa[x]等于x时,就找到了根节点,return x。反之,继续查找。
int get(int x){
if(fa[x]==x) return x;
return get(fa[x]);
}
4.合并
将两个不同元素所在的集合合并为一个集合。
void merge(int x,int y){
fa[get(x)] = get(y);
}
现在,让我们来看看模板的实现
5.思路&例题
P1551 亲戚
题目背景
若某个家族人员过于庞大,要判断两个是否是亲戚,确实还很不容易,现在给出某个亲戚关系图,求任意给出的两个人是否具有亲戚关系。
题目描述
规定:x和y是亲戚,y和z是亲戚,那么x和z也是亲戚。如果x,y是亲戚,那么x的亲戚都是y的亲戚,y的亲戚也都是x的亲戚。
输入输出格式
输入格式:
第一行:三个整数n,m,p,(n<=5000,m<=5000,p<=5000),分别表示有n个人,m个亲戚关系,询问p对亲戚关系。
以下m行:每行两个数Mi,Mj,1<=Mi,Mj<=N,表示Mi和Mj具有亲戚关系。
接下来p行:每行两个数Pi,Pj,询问Pi和Pj是否具有亲戚关系。
输出格式:
P行,每行一个’Yes’或’No’。表示第i个询问的答案为“具有”或“不具有”亲戚关系。
输入输出样例
输入样例#1: 复制
6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6
输出样例#1: 复制
Yes
Yes
No
这道题就可以用并查集来实现。
相当于
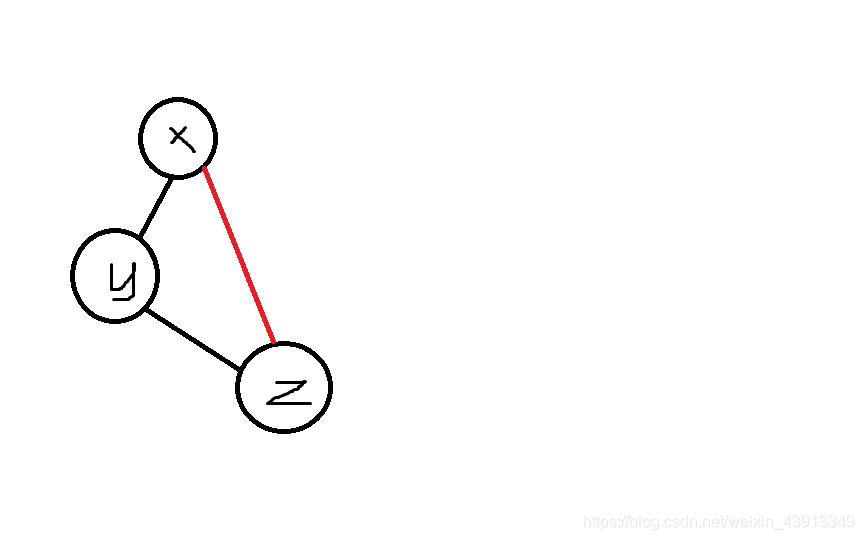
如图,x为y的亲戚,而y又为z的亲戚,所以z为x的亲戚。
然后,就可以搞一波了:
#include<bits/stdc++.h>
using namespace std;
const int maxn=10010;
int n,m,p;
int fa[maxn];
void init(){
for(int i=1;i<=n;i++){
fa[i]=i;
}
}
int get(int x){
if(fa[x]==x) return x;
return get(fa[x]);
}
void merge(int x,int y){
fa[get(x)] = get(y);
}
int main(){
cin >> n >> m>>p;
init();
int x,y;
for(int i=1;i<=m;i++){
cin >> x >> y;
merge(x,y);
}
for(int i=1;i<=p;i++){
cin >> x >> y;
if(get(x)==get(y))cout << "Yes"<<endl;
else cout << "No" <<endl;
}
return 0;
}
但是,不妨想想,这样做会不会太麻烦?
如果z想要知道自己还有没有亲戚,那他就必须问y,才能找到x,这样,会不会耗时间。
再想想,如果有很多亲戚,找起来会不会太慢?
所以,现在看看另一道题
P3367 【模板】并查集
题目描述
如题,现在有一个并查集,你需要完成合并和查询操作。
输入输出格式
输入格式:
第一行包含两个整数N、M,表示共有N个元素和M个操作。
接下来M行,每行包含三个整数Zi、Xi、Yi
当Zi=1时,将Xi与Yi所在的集合合并
当Zi=2时,输出Xi与Yi是否在同一集合内,是的话输出Y;否则话输出N
输出格式:
如上,对于每一个Zi=2的操作,都有一行输出,每行包含一个大写字母,为Y或者N
输入输出样例
输入样例#1: 复制
4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4
输出样例#1: 复制
N
Y
N
Y
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据,N<=10,M<=20;
对于70%的数据,N<=100,M<=1000;
对于100%的数据,N<=10000,M<=200000。
这倒就要用到路径压缩。
如何压缩?
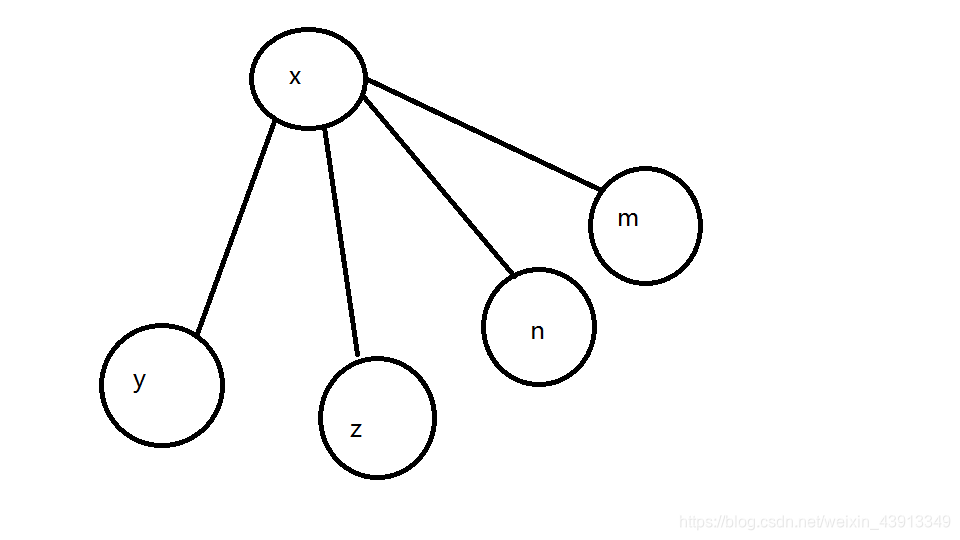
让它们直接找到x,就行了。
所以,只需要改一改
#include<bits/stdc++.h>
using namespace std;
const int maxn=10010;
int n,m;
int fa[maxn];
void init(){
for(int i=1;i<=n;i++){
fa[i]=i;
}
}
int get(int x){
if(fa[x]==x) return x;
return fa[x]=get(fa[x]);
}
void merge(int x,int y){
fa[get(x)] = get(y);
}
int main(){
cin >> n >> m;
init();
int x,y,z;
for(int i=1;i<=m;i++){
cin >> x >> y >> z;
if(x==1){
merge(y,z);
}else if(get(y)==get(z))cout << "Y"<<endl;
else cout << "N" <<endl;
}
return 0;
}
各种各样的并查集
网络交友
Description
在网络社交的过程中,通过朋友,也能认识新的朋友。在某个朋友关系图中,假定 A 和 B 是朋友,B 和 C 是朋友,那么 A 和 C 也会成为朋友。即,我们规定朋友的朋友也是朋友。
现在要求你每当有一对新的朋友认识的时候,你需要计算两人的朋友圈合并以后的大小。
Input
第一行:一个整数 n(n≤5000),表示有 n 对朋友认识。
接下来 n 行:每行输入两个名字。表示新认识的两人的名字,用空格隔开。(名字是一个首字母大写后面全是小写字母且长度不超过 20 的串)。
Output
对于每一对新认识的朋友,输出合并以后的朋友圈的大小。
Sample Input 1
3
Fred Barney
Barney Betty
Betty Wilma
Sample Output 1
2
3
4
#include<bits/stdc++.h>
using namespace std;
const int maxn=10010;
int n,k;
int sz[maxn],fa[maxn];
map<string, int>mp;
void init(){
for(int i=1;i<=n+1;i++){
fa[i]=i;
sz[i]=1;
}
}
int get(int x){
if(fa[x]==x) return x;
else return fa[x]=get(fa[x]);
}
void merge(int x,int y){
int tx=get(x);
int ty=get(y);
if(tx!=ty){
fa[tx]=ty;
sz[ty]+=sz[tx];
}
}
int main(){
cin >> n;
int ans=0;
init();
string s1,s2;
while(n--){
cin >> s1 >> s2;
int x,y;
if((x=mp[s1]) == 0) x = mp[s1] = ++k;
if((y=mp[s2]) == 0) y = mp[s2] = ++k;
merge(x,y);
cout << sz[get(y)] << endl;
}
return 0;
}
昆虫的生活
Description
一天蒜头君正在研究一种稀有昆虫的行为。他们具有两种不同的性别,他假设他们只与异性昆虫互动。因为他们背上都印有数字,所以他们之间的一起互动,在实验室是很容易识别的。
现在给出一些昆虫之间的互动,看看实验是否支持蒜头君的假设–只有异性互动。
Input
第一行输入两个整数 nnn (1≤n≤2000)(1 \le n \le 2000)(1≤n≤2000) , mmm (1≤m≤106)(1 \le m \le 10^6)(1≤m≤106)。其中 nnn 表示昆虫的数目,mmm 表示昆虫互动的关系数量。
接下来会有 mmm 行,每行有两个整数 xxx , yyy (1≤x,y≤n)(1 \le x,y \le n)(1≤x,y≤n)。表示昆虫 xxx 和昆虫 yyy 之间有过互动。
Output
判断蒜头君的假设是否正确,如果正确请输入yes,否则输出no。
Sample Input 1
3 3
1 2
2 3
1 3
Sample Output 1
no
#include<bits/stdc++.h>
using namespace std;
const int maxn=5010;
struct node{
int x,y;
}g[10000010];
int fa[maxn*2];
int n,m;
int init(){
for(int i=1;i<=n*2;i++){
fa[i]=i;
}
}
int get(int x){
if(fa[x]==x)return x;
int r=get(fa[x]);
fa[x]=r;
return r;
}
void merge(int x,int y){
fa[get(x)]=get(y);
}
int main(){
cin >> n >>m;
init();
for(int i=1;i<=m;i++){
cin >> g[i].x >> g[i].y;
}
for(int i=1;i<=m;i++){
if(get(g[i].x)==get(g[i].y)) {
cout <<"no"<<endl;
return 0;
}
merge(g[i].x,g[i].y+n);
merge(g[i].y,g[i].x+n);
}
cout <<"yes";
return 0;
}
关押罪犯
Description
S 城现有两座监狱,一共关押着 NNN 名罪犯,编号分别为 111 ~ NNN。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久,如果客观条件具备则随时可能爆发冲突。我们用 “怨气值”(一个正整数值)来表示某两名罪犯之间的仇恨程度,怨气值越大,则这两名罪犯之间的积怨越多。如果两名怨气值为 ccc 的罪犯被关押在同一监狱,他们俩之间会发生摩擦,并造成影响力为 ccc 的冲突事件。
每年年末,警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表,然后上报到 S 城 Z 市长那里。公务繁忙的 Z 市长只会去看列表中的第一个事件的影响力,如果影响很坏,他就会考虑撤换警察局长。
在详细考察了 NNN 名罪犯间的矛盾关系后,警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配,以求产生的冲突事件影响力都较小,从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨,那么他们一定会在每年的某个时候发生摩擦。
那么,应如何分配罪犯,才能使 Z 市长看到的那个冲突事件的影响力最小?这个最小值是多少?
Input
输入第一行为两个正整数 N(1≤N≤20000)N(1 \le N \le 20000)N(1≤N≤20000) 和 M(1≤M≤100000)M(1 \le M \le 100000)M(1≤M≤100000),分别表示罪犯的数目以及存在仇恨的罪犯对数。
接下来的 MMM 行每行为三个正整数 aj,bj,cja_j,b_j,c_jaj,bj,cj,表示 aja_jaj 号和 bjb_jbj 号罪犯之间存在仇恨,其怨气值为 cjc_jcj。数据保证 1[HTML_REMOVED]aj,bj≤N1[HTML_REMOVED]a_j, b_j \le N1<aj,bj≤N,0[HTML_REMOVED]cj≤1090 [HTML_REMOVED] c_j \le 10^90<cj≤109,且每对罪犯组合只出现一次。
Output
输出共一行,为 Z 市长看到的那个冲突事件的影响力。如果本年内监狱中未发生任何冲突事件,请输出 000。
Sample Input 1
4 6
1 4 2534
2 3 3512
1 2 28351
1 3 6618
2 4 1805
3 4 12884
Sample Output 1
3512
#include<bits/stdc++.h>
using namespace std;
const int maxn = 200100;
const int maxm = 100100;
struct node{
int u,v;
int s;
}e[maxm];
bool cmp(node a,node b){
return a.s>b.s;
}
int fa[maxn*2];
int n,m;
void init(){
for(int i=1;i<=2*n;i++){
fa[i] = i;
}
}
int get(int x){
if(fa[x]!=x) fa[x]=get(fa[x]);
return fa[x];
}
void merge(int x,int y)
{
fa[get(x)] = get(y);
}
int main(){
cin >> n >> m;
init();
for(int i=1;i<=m;i++){
cin >> e[i].u >> e[i].v >> e[i].s;
}
sort(e+1,e+m+1,cmp);
for(int i=1;i<=m;i++){
if(get(e[i].u)==get(e[i].v)){
cout << e[i].s;
return 0;
}else{
merge(e[i].u,e[i].v+n);
merge(e[i].u+n,e[i].v);
}
}
cout << "0";
return 0;
}


void merge(int x,int y){
fa[get(x)] = get(y);
}
您好,请问这一块为什么不是找到x的父节点,复制给fa[y]呢(即fa[get(y)] = fa[get(x)]). 你这样写不让x合并到y中吗?谢谢
大佬,请问昆虫的生活里面,主函数里merge的时候为什么要+n呢?
大佬讲解地好棒啊!
谢谢
%%%