bfs求最短路

视频链接在此！

bfs昨天我们刚刚讲完。
我们今天初识图论，来讲一下bfs求最短路。
我们知道宽搜可以确定点的层次（即每个点离起点的距离。）
那宽搜如何遍历呢？
请看下图：

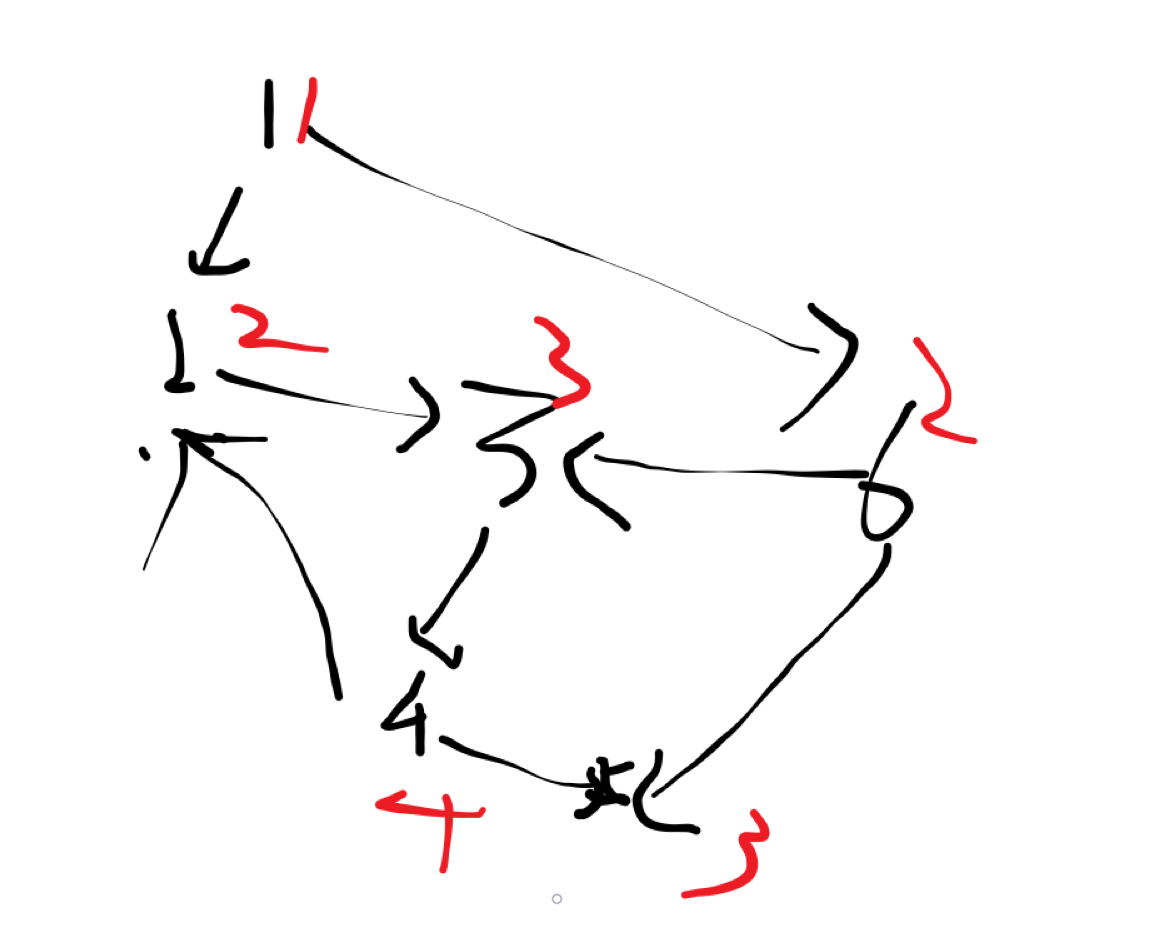
红色数字表示的是每个点离点1的距离。
我们发现：每个点被搜到的次序即每个点离点1的最短路。

6不6？

好我们看些这道题：图中点的层次——bfs最短路
本题是一个最短路问题。
其实解法多了去了。（比如大家熟知的spfa沙发算法）
我们看一下如何来求我们的每个点离点1的距离。
其实还是那句话：模板！
回忆一下宽搜的板子。

while(队列不空)
{
    弹出队头
    拓展队头
}

以及遍历的板子；

for(int i = h[/* # */]; i != -1; i = ne[i])
{
    int j = e[i];
    //blahblahblah
}

那我们结合一下就可以得到：

while(hh <= tt)
{
    int t = q[hh ++];
    for(int i = h[t]; i != -1; i = ne[i])
    {
        int j = e[i];
        //然后的后面有哦
    }
}

接下来我们想一下如何拓展队头。
我们可以先判断一下当前这个点有没有搜到，然后如果没有我们就加一下当前这个点。

if(d[j] == -1)
{
    d[j] = d[t] + 1;
    q[ ++ tt] = j;
}

当然这就需要初始化一下整个数组。
bfs部分完整代码：

int bfs()
{
    memset(d, -1, sizeof d);
    d[1] = 0;//1号点离1号点的距离是0。。。很弱吧
    q[0] = 1;//第一个搜到的点是1，这里用模拟队列，其实STL也行（不香吗？）。
    int hh = 0, tt = 0;
    while(hh <= tt)//模板走起！
    {
        int t = q[hh ++];
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(d[j] == -1)
            {
                d[j] = d[t] + 1;
                q[ ++ tt] = j;
            }
        }
    }
    return d[n];
}

然后加上其他的一些代码就行了。
大家先自己写一遍然后来看看代码h

本题完整代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, m, h[N], e[N], ne[N], d[N], q[N], idx;
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
int bfs()
{
    memset(d, -1, sizeof d);
    d[1] = 0;
    q[0] = 1;
    int hh = 0, tt = 0;
    while(hh <= tt)
    {
        int t = q[hh ++];
        for(int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if(d[j] == -1)
            {
                d[j] = d[t] + 1;
                q[ ++ tt] = j;
            }
        }
    }
    return d[n];
}
int main()
{
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for(int i = 0; i < m; i ++)
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
    }
    cout << bfs() << endl;
    return 0;
}

推荐用时：2.5min
debug：
1. memset没加
2. bfs写错了
3. 注意tt=0
4. 注意q[0]=1
5. 注意d[1]=0

好了今天的分享就到这里了

顺便说一句后面的3天我们将开始复习课。

未经允许，请勿抄袭！

这是我的全部分享！

bye~