算法分析

树状数组示意图如下

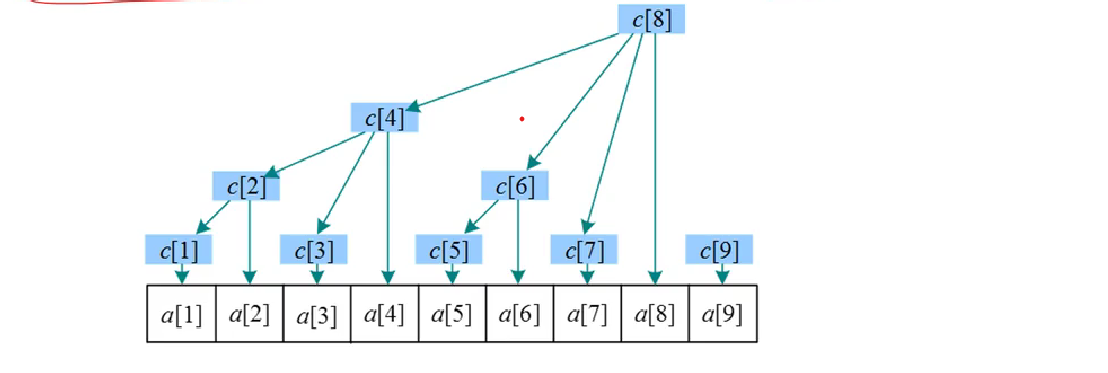
对于树状a，引入的另外一个树状数组c来管理a数组，c也叫管理数组；
可以看出：
c[1]=a[1]
c[2]=a[1]+a[2]
c[3]=a[3]
c[4]=a[1]+a[2]+a[3]+a[4]
c[5]=a[5]
c[6]=a[5]+a[6]
c[7]=a[7]
c[7]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]

区间长度

分析得出：c[i]管理的结点数其实就是lowbit(i),i在二进制下结尾连续个0的数目为k，lowbit(i)=2^k;

前驱和后继

1.直接前驱：c[i] 的直接前驱就是c[i-lowbit(i)],即c[i]左侧紧邻的子树的根；
2.直接后继：c[i] 的直接后继就是c[i+lowbit(i)],即c[i]的父节点；
3.前驱：c[i]左侧所有子树的根；
4.后继：c[i]的所有祖先；

前缀和

前i个元素的前缀和sum[i]等于c[i]加上c[i]的前驱；

点更新

如果a[i]加上d,那么就需要在树状数组中更新c[i]及其后继（都加上d即可）

算法实现

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N=100010;
int a[N],c[N];        //c就是树状数组
int n,m;

int lowbit(int x){      //计算x的最后一位1，求出c[i]的区间长度
    return x & -x;
}

void add(int x,int d){  //点更新,需要更新i所有后继点
    for(int i=x;i<=n;i+=lowbit(i)){    //i+lowbit(i)就是i的直接后继
        c[i]+=d;
    }
}

int sum(int x){         //计算前缀和
    int s=0;
    for(int i=x;i>0;i-=lowbit(i)){  //i-=lowbit(i)就是直接前驱，到0停止
        s+=c[i];
    }
    return s;
}

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        add(i,a[i]);
    }

    while(m--){
        int l,r;
        cin>>l>>r;
        cout<<sum(r)-sum(l-1)<<endl;
    }

    return 0;
}