bfs

同步视频：

同步视频！

bfs

bfs的全称是宽度优先搜索，也叫广度优先搜索，是一种与队列紧密结合的搜索。
比如我们便利一下下面的搜索树。
红色表示搜到的点的层次。

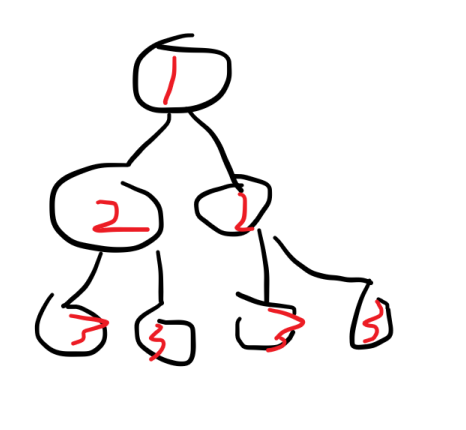
我们可以发现，宽搜是用我们一层一层的搜索构成的。
那我们就可以用队列存储我们搜索到了啥。
然后我们看一下bfs对图的便利好理解下一期的bfs求最短路。

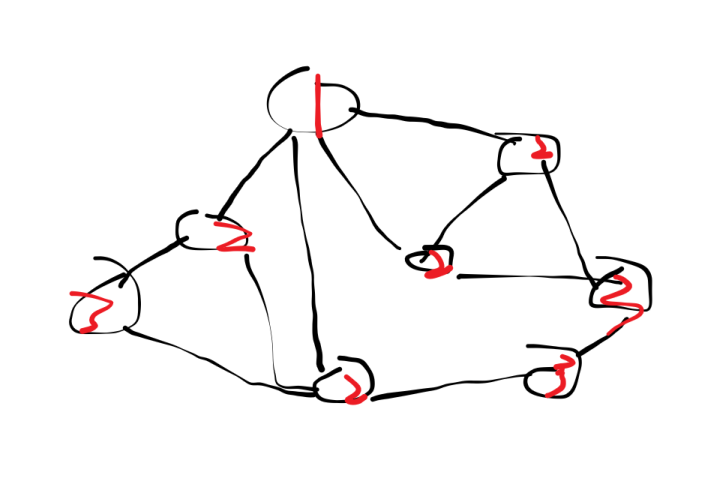
还是一样，图中红色的点表示搜的顺序。

接着我们来复习一下队列。

这里是队列的讲解~

初始化：

int q[N], hh = 0, tt = -1;

插入操作：

q[ ++ tt] = x;

删除操作:

hh ++;

判断队列是否为空：

hh <= tt 

获取：

cout << q[hh] << endl;

以及这里要用到的弹出队头：

auto t = q[hh ++];

接下来我们来说一说宽搜的框架。

其实很弱啊。。。

while(hh <= tt /*队列不空*/)
{
    auto t = q[hh ++];//弹出队头。
    //也可以写成STL版的：
    /*
    auto t = q.front();
    q.pop();
    */
    //拓展队头
    //……
}

来道题：走迷宫

本题可以刚好用DFS来做。

这是层次图：

我们可以这样用d数组存每个点到起始点的距离。
好那条件就是：

1. d[x][y] == -1;//-1表示没走过
2. g[x][y] == 0;

那搜索就来了。
但这里我们拓展队头时不用写四个判断。
我们可以用数组来实现，具体如下：

int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};

然后for循环即可。

分段代码：

1.main：

int main()
{
    cin >> n >> m;
    for(int i = 0; i < n; i ++)
        for(int j = 0; j < m; j ++)
            cin >> g[i][j];
    cout << bfs() << endl;
    return 0;
}

2、bfs准备：

int bfs()
{
    memset(d, -1, sizeof d);
    d[0][0] = 0;
    q[0] = {0, 0};
    int hh = 0, tt = 0;
    /*
    int hh = 0, tt = -1;
    q[ ++ tt] = {0, 0};
    */
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
}

3、框架：

while(hh <= tt)
{
    auto t = q[hh ++];
}

4、拓展队头：

for(int i = 0 ; i < 4; i ++)
{
    int x = t.first + dx[i], y = t.second + dy[i];
    if(x >= 0 && x < n && y >= 0 && y < m && d[x][y] == -1 && g[x][y] == 0)
    {
        d[x][y] = d[t.first][t.second] + 1;
        q[ ++ tt] = {x, y};
    }
}

5、return

return d[n - 1][m - 1];

完整代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 1100;
int n, m, g[N][N], d[N][N];
pair<int, int> q[N * N];
int bfs()
{
    memset(d, -1, sizeof d);
    d[0][0] = 0;
    q[0] = {0, 0};
    int hh = 0, tt = 0;
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
    while(hh <= tt)
    {
        auto t = q[hh ++];
        for(int i = 0; i < 4; i ++)
        {
            int x = t.first + dx[i], y = t.second + dy[i];
            if(x >= 0 && x < n && y >= 0 && y < m && d[x][y] == -1 && g[x][y] == 0)
            {
                d[x][y] = d[t.first][t.second] + 1;
                q[ ++ tt] = {x, y};
            }
        }
    }
    return d[n - 1][m - 1];
}
int main()
{
    cin >> n >> m;
    for(int i = 0; i < n; i ++)
        for(int j = 0; j < m; j ++)
            cin >> g[i][j];
    cout << bfs() << endl;
    return 0;
}

好了这期分享就到这里了（没有作业！）

未经允许，请勿转载！

这是我的全部分享！

bye~