十大背包

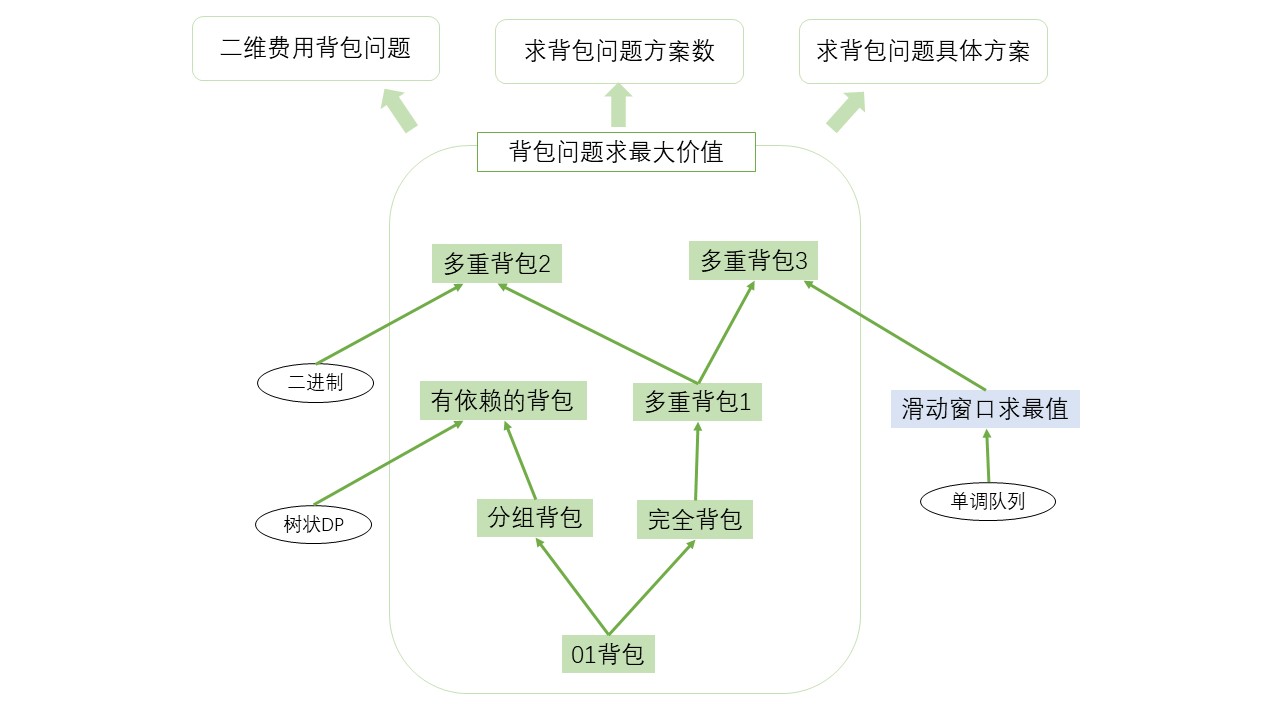
框架图

C++模板

01背包

共 n 个物品，每个物品的重量与价值分别为 $v_i$ 和 $w_i$，用容积为 c 的背包来装，能获得的最大价值是多少？

从前 i 个物品中选，体积不超过 j 的所有选法中，价值最大为多少？ 选择0或1个第 i 个物品

$f(i, j) = max[ f(i-1, j), f(i-1, j-v) + w \quad | \quad j \ge v ]$

#include <iostream>

using namespace std;

const int N = 1010;

int v[N], w[N];  // volumn, worth
int f[N];
int n, m;

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++)
        for (int j = m; j >= v[i]; j --)
            f[j] = max(f[j], f[j-v[i]] + w[i]);

    cout << f[m] << endl;

    return 0;
}

完全背包

共 n 种物品，每种物品的重量与价值分别为 $v_i$ 和 $w_i$，个数均为无限个，用容积为 c 的背包来装，能获得的最大价值是多少？

从前 i 种物品中选，体积不超过 j 的所有选法中，价值最大为多少？ 选择 k 个第 i 个物品

$f(i, j) = max[ f(i-1, j-kv)+kw \quad | \quad k \in [0, +∞) , j \ge kv ]$

令 s = j / v
则f[i][j] = max(f[i-1][j], f[i-1][j-v]+w, ..., f[i-1][j-s*v]+s*w)
得f[i][j-v] = max( f[i-1][j-v] , ..., f[i-1][j-s*v]+(s-1)*w)
因此
f[i][j] = max(f[i-1][j], f[i][j-v]+w)

#include <iostream>

using namespace std;

const int N = 1010;

int v[N], w[N];
int f[N];
int n, m;


int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++)
        for (int j = v[i]; j <= m; j ++)
            f[j] = max(f[j], f[j-v[i]] + w[i]);

    cout << f[m] << endl;

    return 0;
}

多重背包朴素算法

共 n 种物品，每种物品的重量与价值分别为 $v_i$ 和 $w_i$，个数为 $s_i$，用容积为 c 的背包来装，能获得的最大价值是多少？

从前 i 种物品中选，体积不超过 j 的所有选法中，价值最大为多少？ 选择 k 个第 i 个物品

$f(i, j) = max[ f(i-1, j-kv)+kw \quad | \quad k \in [0, s] , j \ge kv ]$

#include <iostream>

using namespace std;

const int N = 110;

int v[N], w[N], s[N];
int f[N][N];
int n, m;

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++) cin >> v[i] >> w[i] >> s[i];

    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= m; j ++)
        {
            f[i][j] = f[i-1][j];
            for (int k = 0; k <= s[i] && j >= k * v[i]; k ++)
                f[i][j] = max(f[i][j], f[i - 1][j - k*v[i]] + k*w[i]);
        }

    cout << f[n][m] << endl;

    return 0;
}

多重背包二进制优化

任意一个 $0 \sim m$ 之间的整数，都可以由 $1, 2, 4, …, 2^{k-1}, m-2^k + 1$ 这些数的组合得到，其中 $2^k - 1 < m <= 2^{k+1} - 1$。

将 $s_i$ 件第 $i$ 类物品，划分为数量分别为 $1, 2, 4, …, 2^{k-1}, s_i-2^k + 1$ 的包裹，每个包裹只有取或不取两种选择，即转化为01背包问题。由以上数学事实可知，转化后的01背包问题的每一种方案都与原来多重背包问题的方案一一对应。

#include <iostream>

using namespace std;

// 多重背包问题中最多1000种物品，每种最多2000个
// 01背包问题中划分为1000*log(2000) ~ 11000个不同的物品
const int N = 11010;

// 背包限制：体积不超过 2000
const int M = 2010;   

int v[N], w[N];  //01背包问题的物品体积、价值
int f[M];
int n, m;

int main()
{
    cin >> n >> m;

    int cnt = 0;  // 01背包问题的物品计数
    for (int i = 1; i <= n; i ++)
    {
        int a, b, s;  //多重背包问题的物品体积、价值、数量
        cin >> a >> b >> s;
        int k = 1;   // k = 1, 2, 4, 8, 16, ...
        while (k <= s)
        {
            cnt ++;
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }
        if (s > 0)  // 最后一项：非2的整次幂
        {
            cnt ++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }

    // 求解01背包问题
    n = cnt;
    for (int i = 1; i <= n; i ++)
        for (int j = m; j >= v[i]; j --)
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;

    return 0;
}

多重背包单调队列优化

$f(i, j) = max[ f(i-1, j-kv)+kw \quad | \quad k \in [0, s] , j \ge kv ]$

f[i][j] = max(f[i-1][j], f[i-1][j-v]+w, ..., f[i-1][j-s*v]+s*w)
f[i][j-v] = max(f[i-1][j-v], ..., f[i-1][j-(s+1)*v]+s*w)
f[i][j-2*v] = ...
f[i][j-3*v] = ...
f[i][j-t*v] = max(f[i-1][j-t*v], ..., f[i-1][j-(s+t)*v]+s*w)
...
f[i][r+s*w] = max(f[i-1][r+s*w], ..., f[i-1][r] + s*w)

其中 r = m % s

首先，使用窗口大小为s的队列，可以求出任意一个的f[i][j-rv]，即求 s+1 个数中最大的那个。

其次，滑动窗口求最大值，比较器是 f[i-1][k] - (k - r)/v*w

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 20010;

int n, m;
int f[N];  // f[k]:  从前i个物品中取，取得物品的价值恰好为k的方案中，价值最大能达到多少
int g[N];  // g[k]:  即 f[i-1][k]
int q[N];  // q[tt]: 窗口内g[k] - (k - j)/v*w最大的元素对应的下标k

int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i ++)
    {
        int v, w, s;
        cin >> v >> w >> s;
        memcpy(g, f, sizeof f);

        // 枚举 r = j % v[i] 的所有情况，就相当于枚举了所有j
        for (int r = 0; r < v; r ++)
        {    
            int hh = 0, tt = -1;

            // k = { r, r + v, r + 2v, ..., j - v, j }
            for (int k = r; k <= m; k += v)
            {
                // 保持窗口大小不超过s
                if (hh <= tt && q[hh] < k - s * v) hh ++;  

                // 求f[i, k]
                if (hh <= tt)  // (k - q[hh])/v 为相差多少个项，从而通过乘 w 确定偏移量
                    f[k] = max(f[k], g[q[hh]] + (k - q[hh]) / v * w);  

                // 在偏移意义上，将所有不大于当前元素的元素从单调队列中删掉
                while (hh <= tt && 
                       g[q[tt]] - (q[tt] - r)/v*w <= g[k] - (k - r)/v*w) 
                    tt --;  

                // 将当前元素插入单调队列末尾
                q[++ tt] = k;
            }
        }
    }

    cout << f[m] << endl;

    return 0;
}

分组背包

共 n 组物品，每组有 $s_i$ 个物品，第 i 组中第 j 个物品物品的重量与价值分别为 $v_{i,j}$ 和 $w_{i, j}$，每组只能选一个物品，用容积为 c 的背包来装，能获得的最大价值是多少？

从前 i 组物品中选，体积不超过 j 的所有选法中，价值最大为多少？ 选择第 i 组第 k个物品

$f(i, j) = max [ f[i-1][j-v_{ik}] + w_{ik} \quad | \quad k \in [0, s_i] ]$ 其中 $v_{i0} = 0, w_{i0}=0$

#include <iostream>

using namespace std;

const int N = 110;

int n, m;
int v[N][N], w[N][N], s[N];
int f[N];

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i ++)
    {
        cin >> s[i];
        for (int j = 1; j <= s[i]; j ++)
            cin >> v[i][j] >> w[i][j];
    }

    for (int i = 1; i <= n; i ++)
        for (int j = m; j >= 1; j --)
            for (int k = 0; k <= s[i]; k ++)
                if (v[i][k] <= j)
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);

    cout << f[m] << endl;

    return 0;
}

有依赖的背包

从以u为根的子树物品中选，体积不超过j的选法中，价值最大为多少？ 选u的子节点son，要求体积不超过k

$f(u, j) := max [ f(u, j-k) + f(son, k) \quad | \quad parent(son) = u, k \le j ]$

#include <iostream>
#include <cstring>

using namespace std;

const int N = 110;

int n, m;
int v[N], w[N];
int h[N], e[N], ne[N], idx;
int f[N][N];  // f[u][j]: 从以u为根的子树物品中选，体积不超过j的选法中，价值的最大值

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

void dfs(int u)
{
    for (int i = h[u]; ~i; i = ne[i])  // 循环组号 i
    {
        int son = e[i];  // 选择第u组的第son个物品
        dfs(son);

        // 分组背包
        for (int j = m - v[u]; j >= 0; j --)  // 循环体积 j
            for (int k = 0; k <= j; k ++)  // 循环决策: son的体积不超过k
            {
                // 第son个物品的价值为f[son][k]
                f[u][j] = max(f[u][j], f[u][j-k] + f[son][k]);
            }
    }

    // 将物品u加进去
    for (int j = m; j >= v[u]; j --) f[u][j] = f[u][j-v[u]] + w[u];
    for (int j = 0; j < v[u]; j ++) f[u][j] = 0;
}

int main()
{
    cin >> n >> m;

    memset(h, -1, sizeof h);
    int root;
    for (int i = 1; i <= n; i ++) // i: 物品编号
    {
        int p;  // p: 物品i所依赖的物品的编号
        cin >> v[i] >> w[i] >> p;
        if (p == -1) root = i;
        else add(p, i);  // p 是 i 的父节点
    }

    dfs(root);

    cout << f[root][m] << endl;

    return 0;
}

二维费用背包

以01背包为例。

从前 i 个物品中选，体积不超过 j 且重量不超过 k 的所有选法中，价值最大为多少？ 选择0或1个第 i 个物品

$f(i, j, k) = max[ f(i-1, j, k), f(i-1, j-v, k - m) + w \quad | \quad j \ge v ]$

#include <iostream>

using namespace std;

const int N = 1010;

int v[N], m[N], w[N];
int f[N][N];
int n, c, wt;

int main()
{
    cin >> n >> c >> wt;
    for (int i = 1; i <= n; i ++)
        cin >> v[i] >> m[i] >> w[i];

    for (int i = 1; i <= n; i ++)
        for (int j = c; j >= v[i]; j --)
            for (int k = wt; k >= m[i]; k --)
                    f[j][k] = max(f[j][k], f[j-v[i]][k-m[i]] + w[i]);

    cout << f[c][wt] << endl;

    return 0;
}

背包问题求方案数

以01背包为例。

若只有其中一个决定使得价值最大，那么方案数与该决定的上一轮方案数一致；若两个决定都能使价值最大，那么方案数为两个决定上一轮方案数之和。

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1010, mod = 1e9 + 7;

int n, c;
int f[N];  // f[i][j]: 从前i个物品中选，体积恰好为j的选法中，价值的最大值
int g[N];  // g[i][j]: 从前i个物品中选，体积恰好为j的选法中，使价值取最大值的选法数量

int main()
{
    cin >> n >> c;

    memset(f, -0x3f, sizeof f);
    f[0] = 0;
    g[0] = 1;

    for (int i = 1; i <= n; i ++)
    {
        int v, w;
        cin >> v >> w;
        for (int j = c; j >= v; j --)
        {
            int maxw = max(f[j], f[j - v] + w);  // 暂存最大价值
            int cnt = 0;   // 记录最大价值方案数
            if (maxw == f[j]) cnt += g[j];  
            if (maxw == f[j - v] + w) cnt += g[j - v];
            g[j] = cnt % mod;  // 题目要求模余
            f[j] = maxw;
        }
    }

    // res: 从前i个物品中选，体积不超过j的选法中，价值的最大值
    int res = 0;
    for (int j = 0; j <= c; j ++) res = max(res, f[j]);

    // cnt: 从前i个物品中选，体积不超过j的选法中，使价值取最大值的选法数量
    int cnt = 0;
    for (int j = 0; j <= c; j ++)
        if (f[j] == res)
            cnt = (g[j] + cnt) % mod;

    cout << cnt << endl;

    return 0;
}

背包问题求具体方案

以01背包为例。

从后向前反推每一次的决策

#include <iostream>

using namespace std;

const int N = 1010;

int n, c;
int v[N], w[N];
int f[N][N];  // f[i][j]: 从前n-i+1个物品中选，体积不超过j选法中，价值的最大值

int main()
{
    cin >> n >> c;

    for (int i = 1; i <= n; i ++) cin >> v[i] >> w[i];

    for (int i = n; i >= 1; i --)
        for (int j = 0; j <= c; j ++)
        {
            f[i][j] = f[i + 1][j];
            if (j >= v[i]) 
                f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
        }

    // f[1][c] 是最大值

    int j = c;
    for (int i = 1; i <= n; i ++)
        if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i])
        {   // 如果选择了第i个物品
            cout << i << ' ';
            j -= v[i];
        }

    return 0;
}