更好的阅读体验

导言

毒瘤题目总是那么多,觉得最小生成树容易?来一道代码巨恐怖的题目练练手吧!

题目描述

原题链接

一群小丑演员，以其出色的柔术表演，可以无限量的钻进同一辆汽车中，而闻名世界。

现在他们想要去公园玩耍，但是他们的经费非常紧缺。

他们将乘车前往公园，为了减少花费，他们决定选择一种合理的乘车方式，可以使得他们去往公园需要的所有汽车行驶的总公里数最少。

为此，他们愿意通过很多人挤在同一辆车的方式，来减少汽车行驶的总花销。

由此，他们可以很多人驾车到某一个兄弟的家里，然后所有人都钻进一辆车里，再继续前进。

公园的停车场能停放的车的数量有限，而且因为公园有入场费，所以一旦一辆车子进入到公园内，就必须停在那里，不能再去接其他人。

现在请你想出一种方法，可以使得他们全都到达公园的情况下，所有汽车行驶的总路程最少。

输入格式

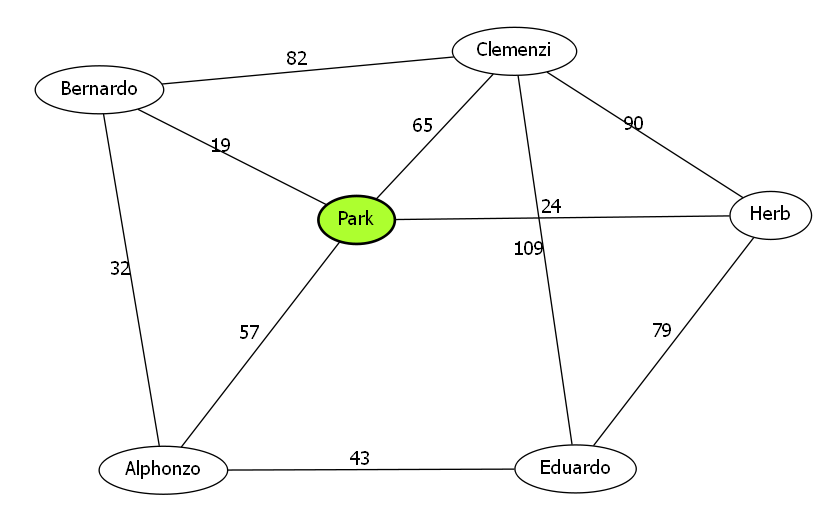
第一行包含整数$n$，表示人和人之间或人和公园之间的道路的总数量。

接下来$n$行，每行包含两个字符串$A、B$和一个整数$L$，用以描述人A和人B之前存在道路，路长为$L$，或者描述某人和公园之间存在道路，路长为$L$。

道路都是双向的，并且人数不超过$20$，表示人的名字的字符串长度不超过$10$，公园用“Park”表示。

再接下来一行，包含整数$s$，表示公园的最大停车数量。

你可以假设每个人的家都有一条通往公园的道路。

输出格式

输出“Total miles driven: xxx”，其中xxx表示所有汽车行驶的总路程。

输入样例：

10
Alphonzo Bernardo 32
Alphonzo Park 57
Alphonzo Eduardo 43
Bernardo Park 19
Bernardo Clemenzi 82
Clemenzi Park 65
Clemenzi Herb 90
Clemenzi Eduardo 109
Park Herb 24
Herb Eduardo 79
3

输出样例：

Total miles driven: 183

解题报告

题意理解

给定一张$N$个点,$M$个边的无向图,求出无向图的一颗最小生成树,但是我们要求一号节点的入度不可以超过给定的整数$S$

也就是一个最小生成树,要求它的一号节点,最多只能和S个节点相连.

思路确定

题意就已经告诉我们,我们的必备算法必然是最小生成树.但是具体的算法流程,我们还得思考一下.

首先,我们要知道两个性质.

1. 一个最小生成树,它的任意一棵子树都是最小生成树.

2. 也就是一个最小生成树,实际上是由很多棵最小生成树构成的.

根据上面所言的性质,我们可以这么考虑这道题目.

首先我们不妨不去考虑这个有特殊限制的一号节点,那么我们忽略掉这个一号节点后.

原图变成了$T$个连通块.
$$ 设T表示为抛去第一号节点后有T个连通块 $$

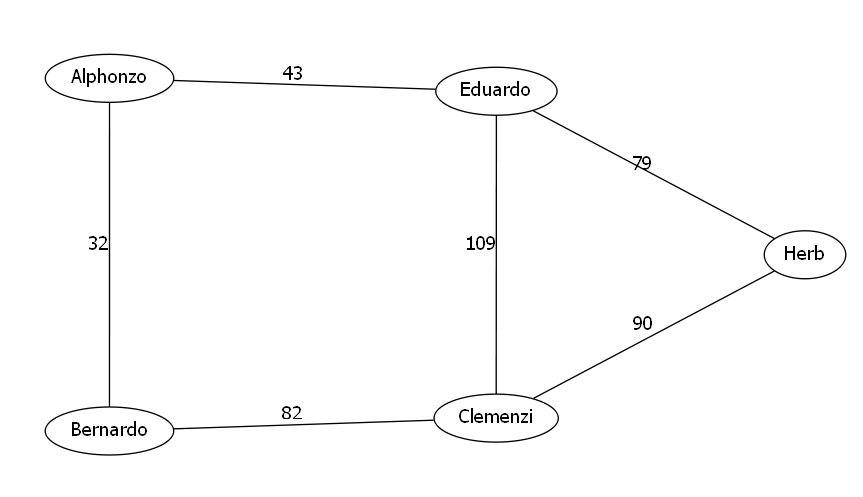
那么我们对于每一个连通块,都可以在这个连通块内部求出它的最小生成树.

我们接下来再来考虑,如何让这些连通块与我们的一号节点相连,构成我们题目的最小生成树.

首先我们很容易求出一个相对较小的生成树.切记不是最小生成树

对于每一个连通块而言,显然要在每一个连通块之中选出一个节点与我们的一号节点的权值最小.即$(1,p)$的权值要尽量小.
$$ p \in 每一个单独的连通块 $$
那么此时,我们发现我们成功将节点们连接在一起了,构成了一个最小生成树,那么现在的问题就是,如何优化我们的生成树,将其变成我们的最小生成树.

我们现在知道和一号节点连接的点,一共有$T$个,但是题目中要求不多于$S$个节点就好了.

分类讨论一下
$$ 若S<T $$
那么我们必然就是无解情况.
$$ 若S=T $$
那么此时我们的生成树,就是我们的最小生成树.
$$ 若S>T $$
我们发现,对于一个节点而言,它不一定要属于自己原本的连通块,它可以和节点$1$相连

我们可以考虑无向图从节点$1$出发的每条边$(1,x,z)$,其中边权为$z$,那么假如说$(1,x)$这条边,它不在当前的生成树内.

那么我们就可以找到从当前生成树总$(1,x)$这条路径上的权值最大边$(u,v,w)$将它删除.

如果说我添加$(1,x,z)$这条边,我就可以删除$(u,v,w)$这条边.

然后我们这颗生成树的权值就可以减少$w-z$.

综上所述,我们每一次从每一个连通块里面找,找到让$w-z$的值最大的点,然后添加$(1,x,z)$,删除$(u,v,w)$

直到
$$ T==S 或者w-z \le 0 $$
也就是不可以加边,或者加边已经木有意义了.

代码解释

这道题目的思路,花了我十五分钟不到的时间理解,然后代码花费了两个晚上的时间,尤其是中途花了一个晚上的时间,打了一百五十多行代码,就在要打完的时候,电脑挂掉了,然后没有保存........................

痛不欲生的我,再次打了一遍.时间就这样多了一晚上

#include <bits/stdc++.h>
using namespace std;
const int N=1010;
#define quick() ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)//读入优化
#define mem(a,b) memset(a,b,sizeof(a))//初始化
#define init() mem(g,0),mem(vis,false),root=cnt=tot2=tot=0,q.clear(),q2.clear()//初始化大军
#define add(a,b,c) g[a][b]=g[b][a]=c//无向图加边
#define mk(a,b) make_pair(a,b)//简便
int tot2,tot,n,m,fa[N],cnt,c,s,root,g[31][31],dis[31][31];
//tot2为边的数量
//tot为点的数量
//cnt为编号的数量
map<string,int> q;//映射关系
map<pair<int,int>,bool> q2;//统计这条边是否出现在最小生成树中
int vis[N];//标记连通块的编号
string a,b;
int find(int x)
{
    return x==fa[x]?fa[x]:fa[x]=find(fa[x]);//并查集找红太阳
}
struct edge1
{
    int x,y,w;
} g2[N];
int cmp (edge1 a,edge1 b)
{
    return a.w<b.w;//最小边排序
}
struct node
{
    int u,v,d;//(u,v)节点权值为d
    inline void inits()
    {
        u=v=0;
        d=-1;
    }
} dp[N];
struct edge2
{
    inline void add_edge(int a,int b,int c)//加入一条边
    {
        g2[++tot2].x=a;//起点
        g2[tot2].y=b;//终点
        g2[tot2].w=c;//权值
    }
    inline int kruskal()
    {
        sort(g2+1,g2+1+tot2,cmp);//排序,找最小
        int ans=0;//我们的目标连通块的连通块编号
        for(int i=1; i<=tot2; i++)
        {
            int x=find(g2[i].x),y=find(g2[i].y);//求出所在连通块
            if (x==1 || y==1 || x==y)//不是目标连通块,或者已经在一起了
                continue;
            fa[x]=y;//合并
            ans+=g2[i].w;//统计
            q2[mk(g2[i].x,g2[i].y)]=true;//这条边出现过
            q2[mk(g2[i].y,g2[i].x)]=true;
        }
        return ans;
    }
} g3;
void read()
{
    quick();
    init();
    cin>>n;
    root=q["Park"]=tot=1;//Park节点就是我们的一号节点
    for(int i=1; i<=n; i++)
    {
        cin>>a>>b>>c;
        if (!q[a])//名字读入
            q[a]=(++tot);//新编号
        if (!q[b])
            q[b]=(++tot);//新编号
        g3.add_edge(q[a],q[b],c);//加边
        add(q[a],q[b],c);//加边
        fa[i]=i;//初始化每个点的父亲节点
    }
    cin>>s;
}
void dfs(int x)
{
    for(int j=2; j<=tot; j++)
        if (g[x][j] && !vis[j])//有边,但是木有被标记
        {
            vis[j]=cnt;
            dfs(j);
        }
}
void pd()//连通块划分
{
    for(int i=2; i<=tot; i++)
        if (!vis[i])
        {
            cnt++;//又来一个
            vis[i]=cnt;
            dfs(i);
        }
}
void dfs(int now,int last)//计算(1,x)路径上最大边
{
    for(int i=2; i<=tot; i++)
    {
        if(i==last || !q2[mk(now,i)])//点重叠,或者没有这条边
            continue;
        if(dp[i].d==-1)//没有来过
        {
            if(dp[now].d>g[now][i])
                dp[i]=dp[now];
            else
            {
                dp[i].u=now;
                dp[i].v=i;
                dp[i].d=g[now][i];
            }
        }
        dfs(i,now);
    }
}
void work()
{
    pd();
    int ans=g3.kruskal();//统计每一个连通块的值
    for(int i=1; i<=cnt; i++)
    {
        int now=0x3f3f3f3f,st=0;//初始值为INF
        for(int j=2; j<=tot; j++)
            if (vis[j]==i)//属于这个连通块
                if (now>g[1][j] && g[1][j]!=0)
                {
                    now=g[1][j];//找到与1相连最小的边
                    st=j;
                }
        ans+=now;//将每一个连通块与1相连
        q2[mk(1,st)]=q2[mk(st,1)]=true;
    }
    int t=cnt;
    while(s>t)
    {
        s--;
        int now=0,idx=0;
        for(int i=1; i<=1100; i++)
            dp[i].inits();
        dfs(1,-1);//求每一个点到1的途中最大边是谁?
        for(int j=2; j<=tot; j++)
        {
            if(now<dp[j].d-g[1][j] && g[1][j])
            {
                now=dp[j].d-g[1][j];//找到最大权值边
                idx=j;
            }
        }
        if (now<=0)//已经不会多优秀了
            break;
        ans=ans-now;
        q2[mk(dp[idx].u,dp[idx].v)]=false;//删除边
        q2[mk(1,idx)]=q2[mk(idx,1)]=true;//添加边
    }
    cout<<"Total miles driven: "<<ans;
}
int main()
{
    read();
    work();
    return 0;
}